임상자료를 이용한 나무구조 분류모형의 성능 비교
Abstract
Objectives:
A classification tree is one of the statistical tools that is widely used in the data mining field. It is useful for making statistical decisions, for example, in medical, biology, and business management area. In this paper, we examine newly developed classification tree algorithms and compare them with real examples in medical study, and provide a guideline to select appropriate methods for data analysis.
Methods:
For the comparison, we used four clinical datasets from UCI (University of California, Irvine) repository. We divide each data to 2/3 training and 1/3 test data set. After fitting the models with various R packages (tree, rpart, party, evtree, CORElearn and randomForest), misclassification rates for training data and test data are calculated separately. Also, specificity and sensitivity are calculated for test data. This procedure is repeated 200 times and compare misclassification rates with one-way analysis of variance and Tukey’s honest significant difference (HSD). Also, specificities and sensitivities are compared.
Results:
In every case, randomForest shows the best performance. For the single tree methods, the performance of methods is different in each data set. evtree show better performance than the other methods in most data sets. Most sensitivities in Breast Tissue and Dermatology data are quite large. rpart and ctree show very low specificity in Dermatology Data.
Conclusions:
Every method has its own characteristic and the performance depends on data. Our study shows that the best single tree methods are different in four example data and evtree shows slightly better performance than the other single tree methods in most data sets. randomForest always shows the best performance, mainly because of using a lot of trees instead of one tree.
Key words: Classification, Tree-structured model, Clinical data analysis
서 론
분류분석(classification)은 설명변수들을 이용하여 관측을 미리 정해진 그룹 중의 하나로 분류하는 규칙을 찾는 분석 방법으로 다양한 방법들이 개발되어 있다. 이들 중 나무구조 분류분석은 비모수적 방법으로 의사결정 규칙을 이용하여 자료를 그룹으로 분류하고 예측하는 분석 방법으로 최종 선택된 의사결정 규칙을 나무구조로 표현한다. 다른 분류분석 방법들에 비하여 다소 예측력이 떨어지는 면이 있음에도 불구하고 널리 쓰이고 있는 가장 큰 이유는 나무구조로 표현되어 분류의 규칙을 쉽게 이해하고 적용할 수 있으며 결과의 해석 또한 이해하기 쉽다는 점으로 자료 분석의 목적이 자료 생성의 구조에 대한 통찰인 경우 유용하게 이용될 수 있다. 임상자료 분석에서 기존의 자료를 이용하여 질병의 발생 원인을 파악하거나 앞으로의 발생 가능성을 예측하고자 하는 경우 나무구조 분류분석이 유용하게 쓰이게 된다.
1963년 처음으로 개발된 회귀나무인 Automatic Interaction Detection (AID) [ 1]을 시작으로 이를 분류나무로 확장시킨 Theta Automatic Interaction Detection (THAID) [ 2], ID3 [ 3] 등의 다양한 나무구조를 이용한 분류분석들이 연구되어 왔다. 1984년에 이르러 제안된 Classification And Regression Tree (CART) [ 4]는 AID와 THAID 방법을 개선한 방법으로 지금까지도 가장 널리 쓰이고 있다. 나무구조 분류분석의 문제점으로는 과적합(over-fitting)과 변수 선택에서의 편의성이 있다. CART에서는 변수 선택의 편의성은 해결하지 못하였으나 과적합을 해결하기 위하여 나무구조의 가지치기 방법을 이용하였다. 설명변수 각각에 대하여 가능한 분리 규칙들을 함께 고려하여 발생하는 변수 선택에서의 편의성을 피하기 위하여 Chi-squared automated interaction detection algorithm (CHAID) [ 5]에서는 범주형 설명변수에 대하여 카이제곱 통계량을 이용하였고, Fast and Accurate Classification Tree (FACT) [ 6]에서는 연속형 설명변수에 대하여 analysis of variance (ANOVA)의 F값을 이용하였다. 또한 90년대에 들어서면서 ID3을 확장시킨 C4.5 [ 7], FACT를 확장시킨 Quick, Unbiased and Efficient Statistical Tree (QUEST) [ 8], Classification Rule with Unbiased Interaction Selection and Estimation (CRUISE) [ 9] 등이 제안되었다. 이들 방법들은 대부분 각 마디에서 자료를 분할하는 방식으로 나무를 확장시켜가며 분할 후 생성되는 새로운 마디에서는 이전과 같은 방식으로 자료를 분할하는 순환적 방법을 이용한다. 조건부 추론을 이용한 나무구조 분류분석(conditional inference tree, ctree) [ 10], 진화 알고리즘(algorithm)을 이용하여 최적의 나무구조를 찾아가는 분류분석(evolutioinary learning of globally optimal tree, evtree) [ 11], 귀납적인 방법으로 나무구조를 확장하는 CORE 모형 [ 12] 등은 이전과는 다른 방식의 새로운 알고리즘으로 나무를 구성하게 되며 이들 방법은 모두 R의 라이브러리(library)로 구현되어 있다. 이들 방법은 최근 제안된 방법으로 아직까지 다양한 비교연구가 진행되지 않고 있어 실제 자료 분석에서 분류방법들을 선택하기 위한 어려움이 있다. 본 연구에서는 분류방법들이 여러 형태의 자료에서 나타내는 성능을 비교하여 자료 분석에서 분류방법의 선택에 대한 가이드(guide)를 제공하고자 한다. 이를 위하여 본 연구에서는 R로 구현되어 있는 최신의 분류나무 알고리즘들의 특성을 살펴보고 이들의 성능을 여러 자료를 이용하여 비교 분석해 보고자 한다.
이론적 배경
나무구조를 이용한 분류분석들
나무구조 분류분석이란 독립변수의 공간을 여러 개로 분할하여 분할한 공간 각각에 하나씩의 범주를 할당하는 방법으로 이진 나무(binary tree)를 가장 많이 이용한다. 이는 학습 표본(learning sample)을 이용하여 독립변수의 공간을 한 번에 2개의 공간으로 분할하고 각각의 공간을 또 다시 2개로 분할하는 방식으로 반복적으로 분할해 나간다. 이러한 관점에서 나무구조 모형을 반복분할(recursive partition) 방법이라고도 부른다.
대부분의 나무구조 모형은 각각의 분할을 위하여 그룹을 가장 잘 분할하는 하나의 설명변수를 선택하고 이를 이용하여 공간을 분할한다. 분할을 멈춘 후에는 분할한 공간 각각에 하나씩의 범주를 할당하게 된다. 이를 위하여 대부분의 방법들에서 모든 설명변수를 동시에 고려하여 최적의 분할을 찾는 전체조사(exhaustive search)를 이용하게 되며 이때 과적합과 변수 선택에서 발생하는 선택편의(selection bias)의 문제가 발생한다. 과적합의 문제는 가지치기(pruning)를 이용하여 어느 정도 해결이 가능하지만 선택편의는 해결이 어려워 나무구조 모형의 설명력에 큰 영향을 미친다.
일반적인 나무구조 분류모형의 알고리즘은 다음과 같이 정의할 수 있다.
1. 설명변수들 중 반응변수가 나타내는 그룹들을 가장 잘 분할하는 설명변수를 하나 선택한다. 2. 선택한 변수를 이용하여 분할규칙을 만들고 이에 따라 두 공간으로 분할한다. 3. 분할한 공간 각각에서 1과 2의 과정을 반복하여 공간을 반복적으로 분할하고 이들 규칙을 나무형태로 정리한다. 4. 공간분할을 마친 후 구성한 나무구조를 가지치기를 이용하여 나무구조를 좀 더 간단하게 정리한다.
위의 일반적인 나무구조 분류모형의 알고리즘에서 설명변수를 선택하는 방법, 선택한 변수를 공간 분할에 이용하는 방법, 그리고 공간 분할 후 나무의 가지를 치는 방법 등을 달리하여 다양한 나무구조를 구성하는 알고리즘들이 제안되었다. 본 연구에서는 가장 널리 쓰이고 있는 CART 방법과 최근 제안된 방법들인 ctree, evtree, 그리고 CORE 방법의 알고리즘을 살펴보고 이들 방법을 비교, 분석해 보고자 한다.
CART (tree, rpart)
CART [ 4]는 각 마디에서 하나의 설명변수를 선택하고 이를 이용하여 두 개로 분리하는 형태의 이진 나무구조를 생성하는 방법으로 의사결정나무 중 가장 널리 쓰이고 있는 방법 중 하나이다. 분할을 위한 순수도 측정을 위해서는 지니지수(Gini index)를 이용하며 나무의 능력을 향상시키는 새로운 분할이 발견될 때까지 나무를 크게 만든 후 교차검증(cross validation)을 이용한 가지치기를 하여 과적합을 막고 최종 나무의 예측력을 높이게 된다. CART의 방법을 R에서 이용할 수 있도록 구현해 놓은 패키지로는 tree와 rpart가 있다. tree와 rpart 모두 CART의 방법을 잘 구현해 놓았으나 몇 가지 차이점이 있다[ 13]. 가장 큰 차이점은 tree의 경우 분류와 회귀나무만을 위한 함수를 제공하고 있다는 점이다. 반면 rpart는 “anova”, “poisson”, “class”, “exp”의 네 가지 옵션을 제공하고 있어 자료에 따라 회귀나무(anova), 분류나무(class), 생존나무(exp), 그리고 포아송 회귀나무(poisson)의 다양한 형태의 나무모형을 이용할 수 있다. tree 패키지의 경우, 나무를 구성하는 tree 함수와 가지치기를 하는 prune.tree 함수를 따로 제공하고 있어 tree 함수만을 이용하여 나무를 구성한 경우 최대 크기의 나무가 되며 prune.tree 함수를 이용하여야 가지치기를 할 수 있다. 반면 rpart 함수에서는 나무구성 및 가지치기를 동시에 제공하고 있어 하나의 함수로 가지치기까지를 마친 최적의 나무구조를 얻을 수 있다. 또한 rpart에서는 결측치를 처리하는 기본 방법으로 비슷한 성질을 갖는 대리변수(surrogate variable)의 값을 이용하여 결측치를 추정하도록 하고 있다. tree 함수에서는 결측치에 대한 각 마디에서 분할을 위해 쓰이는 특정변수의 값이 결측치인 경우에는 추정을 하지 못한다.
또 다른 차이점은 결과에 대하여 저장하고 있는 정보에 대한 것으로 tree 함수는 나무구조의 결과에 대한 중요한 값만을 저장하고 있는 반면 rpart 함수는 나무구조의 결과물뿐 아니라 대리변수에 대한 정보 등 그 이외의 유용한 정보들을 모두 결괏값으로 저장하고 있다. 설명변수에 대한 정보를 저장하는 방식에서도 차이를 보이고 있다. tree의 경우 모든 설명변수에 대한 정보를 가지고 있으며 설명변수가 범주형인 경우에는 범주의 종류를, 그렇지 않은 경우에는 NULL 값을 저장하고 있다. 이와 같은 방법은 설명변수의 수가 많아지는 경우 저장 공간이나 속도에 대한 문제를 야기하게 된다. rpart에서는 모든 설명변수에 대한 정보를 가지고 있는 대신 범주형 변수만을 추려내어 그에 대한 범주의 정보를 저장하고 있어 속도나 저장 공간 면에서 훨씬 효율적인 관리를 할 수 있게 된다.
조건부 추론을 이용한 나무구조 분류분석
조건부 추론을 이용한 나무구조 분류분석은 party 패키지의 ctree 함수에서 이를 구현해 놓았다. 이는 조건부 추론방법에 이론적 바탕을 둔 불편의 반복분할(unbiased recursive partitioning) 방법으로 반응 변수와 설명변수들의 연관성 검정에 대하여 상황에 맞는 통계량을 설정하고 설정 통계량의 조건부 확률분포를 이용하여 유의확률(p-value)을 구한다. 이를 바탕으로 다중검정(multiple testing) 방법을 이용, 유의확률을 보정하고 미리 지정한 유의수준 α를 이용함으로써 가지치기를 대신하여 과적합 문제를 효율적으로 해결하였다. 통계량 대신 유의확률을 기준으로 이용하여 변수의 측정단위가 다름에도 영향을 받지 않게 된다.
그러나 조건부 확률분포를 아는 경우는 거의 없으므로 조건부 몬테칼로(conditional Monte Carlo) 방법을 이용하여 근사적 분포를 계산하고 이를 이용하여 유의확률을 구한다. 각 단계에서 연관성 검정을 위해서 지정하는 유의수준 α는 나무의 크기를 결정하는 중요한 역할을 하게 된다. 사용되는 유의수준은 두 가지의 관점에서 해석할 수 있다. 첫 번째는 각 변수 간의 검정을 위하여 미리 설정한 수준으로 해석하는 것이다. 이러한 관점에서 보면 유의수준은 각 노드(node)에서 모두 독립이라는 가설을 검정하는 데에 대한 오류를 제어하는 값이 된다. 유의수준에 대한 또 다른 해석은 단순히 나무의 크기를 결정하는 초모수(hyperparameter)로 해석하는 것으로 교차검증이나 추가적인 통계 검정으로 계산하는 위험추정량(risk estimate)을 이용하여 추정한다.
진화 알고리즘을 이용하여 최적화하는 나무구조 분류분석
evtree [ 11]는 진화 알고리즘을 이용하여 나무구조의 분류분석의 모형을 최적화하는 함수로 evtree 패키지로 제공되고 있다. 진화 알고리즘은 유전, 돌연변이, 그리고 자연선택과 같은 다윈진화론의 개념들에 의해 개발된 알고리즘으로 모형을 돌연변이와 교차(crossover)라 부르는 변동 연산(variation operator)을 이용하여 반복적으로 수정해나가는 방식이다. 생존선택과정(survivor selection process)에서는 적합함수(fitness function) 또는 평가함수(evaluation function)라고 부르는 값을 기준으로 하여 수정된 모형들 중 최적의 답을 선택하게 된다. 각 마디에서 분류기준을 최적화하고 이를 반복적으로 이용하는 일반적인 나무구조 분류분석과는 달리 나무구조 전체를 광역적으로 고려하여 최적화하는 방법으로 모형의 복잡도와 오류율은 함께 고려한 평가함수를 이용한다. evtree 모형은 설명변수들의 강한 비선형관계나 변수들 간의 고차 교호작용이 있는 경우, 그리고 설명변수들의 다양한 유형에도 적용될 수 있는 모형으로 널리 쓰이고 있다.
CORE
CORElearn [ 12] 패키지는 변수들을 평가하기 위하여 제안된 새로운 기술들을 통합하여 변수들을 평가하고 나무의 마디에서 다양한 종류의 모형을 형성하고 추정하여 나무를 만드는 귀납적 방법을 구현해 놓은 패키지로 나무모형추정을 위하여 CoreModel 함수를 제공하고 있다. 각 마디에서의 변수선택을 위하여 인근 자료를 예측하는 정도를 고려하여 변수를 선택하는 Relief [ 16] 방법과 인근 자료의 영역을 확대한 ReliefF [ 14] 방법을 제안하여 이를 분류나무의 변수 선택에 적용하였다. 이는 지니 지수나 정보 획득량 등 다양한 불순도(impurity)와 변수 선택 기준으로 이용되고 있다. 귀납적 방법으로 만들어진 나무는 이해하기 쉽고 예측력이 좋지만 나무 모형의 구성을 위하여 대량의 자료 저장 공간과 계산시간을 시간을 필요하기 때문에 minimum description length (MDL) [ 15] 원리를 함께 이용하여 메모리와 시간을 절약한다. 나무를 성장시키는 과정에서 마디에 지정된 최소 개수의 자료가 남을 경우나 마디에서의 분산이 전체 자료의 분산을 고려하여 지정된 최소 분산에 도달할 경우에 나무의 성장을 멈춘다.
랜덤 포레스트
랜덤 포레스트 [ 16]는 Breiman에 의해 2001년에 개발된 방법으로 기존의 의사결정나무의 불안정성과 정밀도가 떨어지는 점을 보완하기 위하여 샘플링 기법을 이용하는 것이다. 이는 자료를 샘플링(sampling)하여 여러 개의 의사결정나무로 확장시킨 후 여러 개의 나무로 확장시킨 후 이들의 결과를 통합하는 방법으로 기존의 의사결정나무 하나로 추정을 하는 데에서 오는 불안정성을 보완하고 있다. randomForest는 랜덤 포레스트 방법을 구현해 놓은 R 패키지로 다음과 같은 방법으로 실행된다.
1. 원 자료에서 복원 추출로 랜덤하게 원 자료 수만큼의 표본을 뽑는다. 뽑은 표본들은 나무를 성장시키기 위한 학습 자료가 된다. 2. 자료에 총 M개의 입력변수가 있다면, 각 노드에서 M개 중 랜덤하게 m개의 변수를 고른다. 그리고 m개의 입력변수 중 노드를 가장 잘 나누는 변수를 찾는다. m의 수는 나무들을 성장시키는 동안 일정하게 유지한다. 3. 각 나무는 최대 범위까지 성장시키며 가지치기는 하지 않는다. 4. 성장된 나무들의 결과를 결합하고 다수결 원칙을 적용하여 최종 의사결정 규칙을 만든다.
앞에서 설명한 5가지의 나무구조들에서 하나의 나무구조를 이용하는 것과는 달리 랜덤 포레스트 방법에서는 샘플링 기법을 이용하여 다수의 나무구조를 이용하므로 안정성과 정확도 면에서 앞의 방법들과는 확연히 다른 성능을 보이게 된다.
연구 방법
성능비교 방법
본 연구에서는 앞에서 살펴본 6가지의 나무구조를 이용한 분류분석 방법들을 여러 가지 임상자료에 적용하여 이들의 성능을 살펴보고자 한다. 예제에서는 통계학에서 분류분석을 설명하기 위하여 가장 널리 쓰이고 있는 Iris 자료를 이용하여 6가지 분류방법의 특징을 살펴보았다. 먼저 자료를 층화추출을 이용하여 랜덤하게 2/3의 학습 자료와 1/3의 테스트 자료로 나눈 후 학습 자료를 이용하여 모형을 추정한 후 학습 자료의 오분류율과 테스트 자료의 오분류율을 계산하였다. 각 분류분석 방법들에 따른 오분류율의 차이를 통계적으로 알아보기 위하여 일원분산분석과 Tukey의 사후검정을 이용하였다. 또한 각 범주별 민감도(sensitivity)와 특이도(specificity)를 계산하여 분석 방법들의 성능을 비교하였다.
모든 분석에는 R version 3.2.3를 이용하였으며 tree (version 1.0-37), rpart (version 4.1-10), party (version 1.0-25), evtree (version 1.0-0), CORElearn (version 1.47.1), 그리고 randomForest (version 4.6-12) 패키지를 이용하였다. 또한 본 연구에서 이용되고 있는 모든 자료는 분류 분석의 방법 비교를 위하여 널리 쓰일 수 있도록 UCI Machine Learning repository ( http://archive.ics.uci.edu/ml)에 공개되어 있는 자료들로 이들 중 임상 관련 자료를 선택한 것이다.
예제를 이용한 성능비교
이론적 배경에서 살펴본 분류나무 방법들의 특징을 좀 더 자세히 비교해 보기 위하여 Iris 자료와 파킨슨 자료를 이용하였다. 자료의 공간을 분할하는 관점에서 비교를 하기 위하여 널리 알려진 Iris 자료를 이용하였으며 많은 변수를 가지고 있는 자료의 분류 결과를 비교하기 위하여 파킨슨 자료를 이용하였다. 각 나무구조에서 공간상의 자료가 분할되는 방식을 비교하는 것이 목적이므로 여러 나무구조의 결과를 통합하여 결과를 내는 랜덤 포레스트 방법을 제외하고 하나의 나무구조로 표현되는 방법들만을 비교하고자 한다.
Iris 자료
Iris 자료는 1936년 Ronald Fisher에 의해 소개된 자료로 분류분석 방법을 설명하기 위하여 가장 많이 이용되는 자료로 R에서 제공하고 있는 자료(iris)를 이용하였다. 이는 세 종류의 Iris, setosa, versicolor, verginica 각각에 대하여 50개씩의 꽃을 선택하여 꽃잎의 길이(Petal. Length)와 꽃잎의 폭(Petal.Width), 꽃받침의 길이(Sepal.Length)와 꽃받침의 폭(Sepal.Width)을 측정한 것이다. Iris 자료를 이용하여 5가지의 함수로 나무구조 분류분석을 시행하였다. 5가지 함수들 모두 최종 선택된 나무구조에서 Petal.Length와 Petal.Width 변수만을 사용하고 있다. Figure 1은 각 분류나무의 공간분할 결과를 Petal.Length와 Petal. Width의 산점도 위에 나타낸 것이다. tree와 CoreModel 함수는 비슷한 결과를 보이고 있으며 rpart와 ctree 함수가 비슷한 결과를 보이고 있다. tree, rpart, 그리고 CoreModel 함수들은 각 노드에서 분할을 위한 기준으로 관측 값들 사이의 중앙값을 이용하는 반면 ctree와 evtree는 관측 값 자체를 이용하는 경향이 있음을 알 수 있다. evtree는 나머지 4가지의 방법과는 확연히 다른 모습의 분할을 보이고 있다.
파킨슨 자료
파킨슨 자료는 파킨슨병에 걸린 사람들과 건강한 사람들의 생체의학 음성측정의 범위를 구한 자료이다. 이 자료조사의 주목적은 음성측정 자료를 이용하여 건강한 사람(48명)과 파킨슨병에 걸린 사람(174명)들을 분류하기 위한 모형을 만드는 것이다. 나무구조의 분류분석은 이와 같은 목적에 부합하는 분석 방법으로 최종 모형의 선택 후 분류 기준을 쉽게 설명할 수 있게 된다. 자료의 정보는 Table 1과 같다.
Figure 2는 9개의 변수를 이용하여 파킨슨병의 여부를 분류하기 위하여 파킨슨 자료를 5가지 분류나무를 위한 함수에 적용한 결과를 나무그림으로 나타낸 것이다. rpart 패키지는 나무구조의 결과를 그리기 위한 함수를 제공하고 있으며 tree와 CORElearn 패키지에서는 rpart의 함수를 이용하여 그림을 그릴 수 있도록 함수를 제공하고 있다. Figure 1A와 Figure 1E의 그림은 rpart에서 제공하는 방식을 이용한 것으로 최종 마디의 1은 파킨슨병 환자로, 0은 건강한 사람으로 분류되는 것을 의미한다.
최근 개발된 party 패키지는 기존의 rpart에서 제공하고 있는 나무구조의 그림을 좀 더 알아보기 쉬운 형태로 그려주기 위한 함수를 제공하고 있으며 ctree 함수 결과뿐 아니라 rpart와 evtree의 결과에도 이용할 수 있도록 제공되어 있다. Figure 1B- D의 그림은 party 패키지에서 제공하는 함수를 이용한 것으로 최종 마디에서 검은 부분은 파킨슨 질병환자의 비율을, 회색 부분은 건강한 사람의 비율을 나타낸다. 모든 함수이용에서 기본으로 제공되고 있는 옵션만을 사용하였다. Figure 1A는 tree 함수의 최종결과나무로 5가지 함수의 결과 중 가장 복잡한 나무구조를 가지고 있다. 오분류율은 5.6%이다. Figure 1B는 rpart 함수의 결과로 tree의 결과보다는 간단한 나무구조를 가진다. 오분류율은 7.2%이다. ctree 함수의 결과인 Figure 1C는 결과들 중 가장 간단한 나무구조를 가지고 있으며 오분류율도 13.3%로 가장 높다. Figure 1D는 evtree 함수의 결과로 rpart의 결과와 비슷한 정도의 복잡도를 갖는 나무구조를 나타내고 있으며 오분류율도 6.2%로 낮다. Figure 1E는 CoreModel 함수의 결과로 다소 복잡한 구조를 가지고 있으며 오분류율은 5.1%로 가장 낮다. ctree의 결과 나무가 가장 단순한 구조이나 가장 높은 오분류율을 보이고 있으므로 나무구조의 확장이 너무 일찍 멈추어 좀 더 복잡한 나무로의 확장이 필요함을 알 수 있다. 이는 나무의 크기를 결정하는 유의수준 α 값을 조절하여 좀 더 확장할 수 있도록 하는 것이 필요하다. evtree를 제외한 모든 방법에서는 첫 번째 마디에서 PPE 변수를 이용하여 분류를 하였으며 MDVP.Fhi.Hz, MDVP.Shimmer, 그리고 MDVP.Fo.Hz 변수를 주로 이용하였다. 최종 결과는 가지치기의 정도는 다르지만 분류 기준은 비슷한 구조를 보이고 있다. 이와는 달리 evtree는 첫 번째 마디에서 HNR 변수를 이용하며 그 이후의 마디에서는 다른 나무들과 비슷한 PPE와 MDVP.Fo.Hz 변수를 이용하고 있다.
분류나무 분석 결과 PPE 값이 0.134보다 크고 MDVP.Shimmer 값이 0.019보다 크면 파킨슨 질병으로 분류되며 PPE 값이 크고 MDVP. Shimmer 값이 0.019보다 작더라도 MDVP.FO.Hz 값이 117.2보다 크면 파킨슨 질병으로 분류된다. 또한 HNR 값이 25.445보다 작고 PPE 값이 0.134보다 큰 경우와 HNR 값이 25.445보다 크더라도 MDVP.Fo.Hz 값이 중간크기의 값(117.226-188.62)이면 파킨슨 질병으로 분류된다. 이와 같이 의사결정 분류나무를 이용하면 질병 분류를 위한 기준을 쉽게 이해할 수 있게 된다.
분석 결과
임상자료를 이용한 나무구조 분류모형의 성능 비교
나무구조 분류나무의 성능을 좀 더 심도 있게 비교해보기 위하여 UCI Machine Learning repository에서 제공하고 있는 4가지의 임상자료를 이용하였다. 임상자료의 특징들은 Table 2에 정리되어 있다. 각 자료에 대하여 2/3의 학습 자료와 1/3의 테스트 자료로 나눈 후 학습 자료를 이용하여 모형을 추정하고 이를 이용하여 학습 자료의 오분류율과 테스트 자료의 오분류율을 각각 구하였다. 5가지의 함수에 대하여 이를 각각 200번 반복한 결과를 정리, 비교하였다.
유방암 세포조직 자료
여러 주파수에서 측정된 유방조직의 임피던스 값을 이용하여 유방암세포 조직의 종류를 분류하기 위하여 수집된 총 106개의 측정 자료로 I0 (제로 주파수에서의 임피던스 값), PA500 (500 kHz에서의 위상각), HFS (위상각의 고주파 슬로프), DA (스펙트럼 사이의 임피던스 거리), Area (스펙트럼 지역), A/DA (DA에 의해 정규화된 영역), Max IP (스펙트럼의 최댓값), DR (I0와 실제 최대 주파수 포인트 부분과의 거리), 그리고 P (스펙트럼 곡선의 길이)의 9개 설명변수로 이루어져 있으며 반응변수는 6개의 암세포 조직종류로 21개의 Carcinoma, 15개의 Fibroadenoma, 18개의 Mastopathy, 16개의 Glandular, 14개의 Connective, 그리고 22개의 Adipose이다.
Table 3은 자료들의 학습 자료 결과를, Table 4는 테스트 자료의 결과를 정리해 놓은 것이다. 학습 자료의 결과는 randomForest, tree, evtree, CoreModel, rpart, 그리고 ctree 순으로 평균 오분류율이 낮았다. ctree는 타 함수들과 비교하여 오분류율이 높아 유방암 세포조직 자료에 모형이 잘 적합되지 않는다고 판단된다. 테스트 자료의 결과에서도 randomForest가 가장 낮은 평균 오분류율을 보이고 있으며 tree가 그 다음으로 낮은 평균 오분류율을 보이고 있다. part, CoreModel, 그리고 evtree의 오분류율은 비슷하였다. ctree는 테스트 자료에서도 타함수들과 비교하여 떨어진 예측력을 보이고 있다. 또한 tree의 경우 테스트 자료의 오분류율이 학습 자료에서의 오분류율의 2배 이상이 되고 있으며 다른 함수들도 테스트 자료의 오분류율이 학습 자료의 오분류율보다 훨씬 크다는 것을 확인할 수 있다.
분산분석 결과 6가지의 분류분석에서 테스트 자료의 오분류율은 차이( F = 46.338, p < 0.0001)를 보이고 있으며 Tukey의 사후검정을 통하여 randomForest가 가장 좋은 성능을, tree, CoreModel, rpart, 그리고 evtree가 그 다음으로 비슷한 성능을 보이고 있음을 확인할 수 있었다. 그리고 ctree가 가장 좋지 않은 성능을 보이고 있음을 확인할 수 있었다( Table 5). 이는 Figure 3A의 상자그림에서도 확인할 수 있다.
Table 6은 200개의 테스트 자료에서 각 범주별로 계산된 민감도와 특이도의 평균을 구한 것이다. Adipose, Carcinoma, 그리고 Connective의 경우 0.7 이상의 높은 민감도를 보이고 있으며 Glandular의 경우도 0.56-0.66의 민감도를 보이고 있다. 그러나 Fibro adenoma와 Mastopathy의 경우 0.4 이하의 낮은 민감도를 보이고 있으며 ctree의 경우 Fibro adenoma에 대하여 0.07로 아주 낮은 민감도를 보이고 있다. 이를 통하여 ctree 방법의 경우 Fibro adenoma를 판별하지 못한다고 결론 내릴 수 있다. 특이도의 경우 Fibro adenoma를 제외한 대부분의 범주에서 민감도에 비하여 낮은 값을 보이고 있다. 특히 Adipose에서의 민감도가 ctree는 0.03, rpart는 0.06으로 매우 낮은 것을 볼 수 있다.
피부병 자료
편평 상피 질환(Erythemato-Squamous diseases)의 감별 진단은 피부과에서 중요한 문제로 대부분 다른 질병과 함께 나타나거나 다른 질병과 비슷한 조직 병리학적 특징을 나타내기 때문에 진단에 어려움이 있다. 피부병 자료(Dermatology data)는 6가지 다른 종류의 피부병을 가진 366명의 환자로부터 편평 상피 질환에 관련된 임상적, 조직 병리학 측정을 얻은 자료로 12가지 임상 측정치와 22가지의 조직 병리학 측정치로 구성되어 있다. 결측치를 가지고 있는 8명을 제외한 358명의 환자를 대상으로 분석을 하였으며 이들은 건선(psoriasis) 환자 111명, 지루성 피부염(seborrheic dermatitis) 환자 60명, 편병태선(lichen planus) 환자 71명, 장미색 비강진(pityriasis rosea) 환자 48명, 만성 피부염(chronic dermatitis) 환자 48명, 모공성 홍색 비강진(pityriasis rubra pilaris) 환자 20명으로 구성되어 있다.
피부병 자료에서 학습 자료의 평균 오분류율은 randomForest, evtree, tree, rpart, CoreModel, 그리고 ctree 순으로 낮았다. 전반적으로 모든 패키지의 오분류율이 낮았다. 테스트 자료의 결과에서는 evtree에서 가장 낮은 오분류율을 보이고 있으며 rpart가 그 다음으로 낮은 오분류율을 나타내고 있다. tree와 CoreModel은 비슷한 성능을 보이고 있으며 ctree는 15.5%로 타 함수의 두 배에 가까운 오분류율을 보이고 있다. CoreModel 함수에서는 학습 자료 오분류율과 테스트 자료 오분류율의 차이가 가장 작게 나타나며 ctree 또한 큰 차이를 보이지 않고 있다. 그러나 tree나 evtree 함수에서는 테스트 자료의 오분류율이 학습 자료의 오분류율의 두 배 정도로 큰 차이를 보이고 있다.
분산분석 결과 Breast tissue data에서와 마찬가지로 6가지의 분류분석에서 테스트 자료의 오분류율은 차이( F =149.52, p < 0.0001)를 보이고 있으며 Tukey의 사후검정을 통하여 randomForest가 가장 좋은 성능을 보이고 있으며 evtree, CoreModel, rpart, 그리고 tree가 그 다음으로 비슷한 성능을 보이고 있음을 확인할 수 있었다. 그리고 ctree가 가장 좋지 않은 성능을 보이고 있음을 확인할 수 있었다( Table 6). 이는 Figure 3B의 상자그림에서도 확인할 수 있다.
Table 7은 200개의 테스트 자료에서 각 범주별로 계산된 민감도와 특이도의 평균을 구한 것이다. 모든 방법의 모든 범주에서 0.8 이상의 높은 민감도를 보이고 있으며 특히 randomForest 방법은 psoriasis, lichen planus, chronic dermatitis에서는 1의 민감도를 보이고 있다. 특이도의 경우 tree, evtree, CoreModel, 그리고 randomForest에서는 0.8 이상의 높은 특이도를 보이고 있다. 그러나 rpart와 ctree의 경우 대부분 0.2 이하의 낮은 민감도를 보이고 있으며 psoriasis의 경우 0.04로 매우 낮은 민감도를 나타내고 있다.
심장질환 자료
심장질환 자료는 환자의 정보와 의학적 측정치를 이용하여 심장병의 유무를 파악하기 위하여 Budapest의 Hungarian Institute of Cardiology, Zurich와 Basel의 University Hospital, 그리고 Long Beach and Cleveland Clinic Foundation의 V.A. Medical Center로부터 수집된 자료로 본 연구에서는 V.A. Medical Center로부터 수집된 자료만을 이용하였다. 환자의 나이(age), 성별(sex), 가슴 통증의 종류(cp), 혈압(trestbps), 콜레스테롤 수치(chol), 공복혈당의 정도(fbs), 심전도 결과(restcg), 최대 달성 심박수(thalach), 운동 유발 협심증의 유무(exang), 운동에 의해 저하되는 ST 수치(oldpeak), 격렬한 운동에서의 ST 기울기 방향(slope), 형광 투시법에 의해 착색되는 주요 혈관 수(ca), 그리고 결함 여부(thal)를 나타내는 13개의 설명변수를 이용하여 심장병의 정도를 0부터 4까지로 표현된 심장병의 정도를 예측하기 위해 5가지의 의사결정나무를 위한 함수를 이용하였다.
심장질환 자료의 학습 자료 분석 결과 randomForest, tree, rpart, evtree, CoreModel, 그리고 ctree 순으로 평균 오분류율이 낮았다. 대체적으로 오분류율이 다른 데이터에 비해 높은 편이었다. 테스트 자료 분석 결과는 randomForest, evtree, rpart, ctree, CoreModel, 그리고 tree 순으로 평균 오분류율이 낮았다. 평균 오분류율이 40% 이상으로 다른 자료에 비하여 오분류율이 매우 높은 편이었다. tree는 학습 자료 분석 결과에서는 두 번째로 오분류율이 낮았으나 테스트 자료에서는 가장 높은 오분류율을 보여 학습 자료와 테스트 자료에서의 성능에서 큰 차이를 보이고 있다. ctree의 경우 학습 자료 오분류율은 가장 높으나 테스트 자료의 오분류율은 다른 방법들과 비교하여 크게 다르지 않음을 확인할 수 있다.
분산분석 결과 6가지의 분류분석에서 테스트 자료의 오분류율은 차이( F =37.763, p < 0.0001)를 보이고 있으며 Tukey의 사후검정을 통하여 randomForest가 가장 좋은 성능을 보이고 있으며 그 다음으로는 evtree가 좋은 성능을 보이고 있음을 확인할 수 있었다. 나머지 4가지 방법들은 그 다음으로 비슷한 성능을 보이고 있다( Table 6). 이는 Figure 3C의 상자그림에서도 확인할 수 있다.
Table 8은 200개의 테스트 자료에서 각 범주(심장병의 정도를 범주로 간주)별로 계산된 민감도와 특이도의 평균을 구한 것이다. 심장병의 유무를 나타내는 범주 0에서는 0.8 이상의 높은 민감도를 보이고 있어 심장병이 없는지에 대한 예측력은 좋은 것을 알 수 있다. 그러나 특이도가 모든 방법에서 0.2 이하로 낮게 나타나고 있음을 볼 수 있다. 심장병의 정도가 심해짐에 따라 민감도가 낮아지는 경향을 보이고 있으며 특이도는 민감도보다는 높은 경향을 보이고 있다.
흉부외과 자료
흉부외과 자료는 2007년부터 2011년까지 폴란드의 브로츠와프 흉부 외과 센터(Wroclaw Thoracic Surgery Centre)에서 폐암으로 인해 주요 폐 절제술을 받은 환자로부터 수집된 것으로 흉곽 수술 후 1년 이내 사망하는 폐암 환자의 사망 원인을 파악하기 위한 것이다. 400명의 1년 이내 사망 환자와 70명의 1년 이상 생존 환자로부터 수집된 자료로 종양 진단 코드(DGN), 폐활량(PRE4), 숨을 내쉬는 양(PRE5), 행동 상태(PRE6), 수술 전의 고통 여부(PRE7), 수술 전 각혈 여부(PRE8), 수술 전 호흡 곤란 여부(PRE9), 수술 전 기침의 여부(PRE10), 수술 전 쇠약함의 여부(PRE11), 원 종양의 사이즈 정도(PRE14), 제2형 당뇨병 여부(PRE17), 6개월 내의 심근경색 여부(PRE19), 말초 동맥 질환의 여부(PRE25), 흡연 여부(PRE30), 천식 여부(PRE32) 그리고 환자의 수술 당시 나이(AGE)에 대한 정보가 있다.
흉부외과 자료의 학습 자료 분석 결과 tree, rpart, CoreModel, ctree, 그리고 evtree 순으로 평균 오분류율이 낮았다. 테스트 자료 분석 결과는 ctree, CoreModel, evtree, rpart, 그리고 tree 순으로 평균 오분류율이 낮았다. 전체적으로 학습 자료와 테스트 자료의 오분류율 순위에서 차이를 보이고 있다. 다른 자료에서 대부분 높은 오분류율을 보인 ctree 함수는 흉부외과 자료에서는 낮은 평균 오분류율을 보이고 있다. 흉부외과 자료에서도 심장질환 자료에서와 마찬가지로 ctree의 경우 학습자료 오분류율은 가장 높으나 테스트 자료의 오분류율은 다른 방법들과 비교하여 크게 다르지 않음을 확인할 수 있다.
분산분석 결과 6가지의 분류분석에서 테스트 자료의 오분류율은 차이( F =132.31, p < 0.0001)를 보이고 있으나 Tukey의 사후검정의 결과는 다른 자료들과는 다른 양상을 보이고 있다. randomForest와 ctree가 비슷한 정도로 가장 좋은 성능을 보이고 있으며 그 다음으로는 CoreModel이 좋은 성능을 보이고 있다. 그 다음은 evtree와 rpart 이며 tree가 가장 좋지 않은 성능을 보이고 있다( Table 6). 이는 Figure 3D의 상자 그림에서도 확인할 수 있다.
Table 9는 200개의 테스트 자료에서 각 범주별로 계산된 민감도와 특이도의 평균을 구한 것이다. Alive 범주에서는 매우 낮은 민감도와 매우 높은 특이도를 보이고 있으므로 Dead 범주는 잘 예측을 하지만 Alive 범주는 잘 예측하지 못하고 있음을 알 수 있다.
결론 및 토의
본 논문에서는 나무구조 분류분석을 위하여 개발된 R 패키지들을 알아보고 이를 임상자료에 적용하여 패키지들의 특성과 성능을 파악, 비교해 보았다. tree와 rpart는 가장 널리 사용되는 CART 알고리즘을 기반으로 하는 나무구조 분류분석을 구현해 놓은 패키지로 같은 알고리즘을 기반으로 하고 있으나 구현에 있어서 차이를 보이고 있다. party 패키지는 조건부 추론을 이용한 나무구조를 추정하기 위한 알고리즘을 구현해 놓은 패키지로 이를 위하여 ctree 함수를 제공하고 있다. 또한 나무구조를 좀 더 보기 좋은 형태로 시각화하기 위한 함수를 제공하고 있다. evtree는 진화 알고리즘을 이용한 나무구조를 위한 패키지로 evtree 함수로 구현되어 있고, CORElearn은 귀납적 방법을 이용한 방법으로 CoreModel 함수로 구현되어 있다. randomForest는 앙상블 기법을 이용하여 다량의 나무모형을 생성한 후 이들을 통합한 결과를 이용하는 방법으로 하나의 나무모형을 이용하는 다른 방법들에 비해 월등히 좋은 성능을 보이게 된다.
각 방법의 오분류율은 분석에 사용된 자료별로 큰 편차를 보였다. randomForest 방법은 모든 자료에서 가장 좋은 성능을 보이고 있으며 tree는 전반적으로 학습 자료를 사용하여 계산한 오분류율은 낮은 것에 비하여 테스트 자료를 사용해 계산한 오분류율은 높아 적합도에 비하여 예측력이 떨어진다는 것을 알 수 있었다. tree와 같은 CART 알고리즘의 rpart는 비교적 적합도는 떨어졌으나 좋은 예측력을 보였다. ctree는 비교한 5가지 패키지 중에서 적합도와 예측력 모두 가장 좋지 않았으나 적합도와 예측력의 차이는 다른 방법들에 비하여 가장 작았다. 실제 자료의 분석 결과 조건부 추론을 이용한 알고리즘의 나무 모형은 분류분석을 수행하는 데 큰 도움이 되지 못하였다. evtree는 나머지 패키지들 중 평균적으로 가장 좋은 예측력을 보였다. evtree의 진화 알고리즘이 예측력을 향상시키는 데 도움을 주었다고 볼 수 있다. CoreModel은 자료에 따라 성능의 편차가 컸으며 rpart와 tree는 대부분의 자료에서 오분류율 편차를 보이고 있으므로 CART 알고리즘을 사용한 패키지의 성능이 안정적이라고 판단할 수 있다. 자료별 편차가 가장 큰 것은 CoreModel 함수로 가장 성능이 불안정 적이었다. 자료 분석 결과를 종합해보면 randomForest를 제외한 방법에서는 evtree가 우수한 성능을 보이고 있다는 것을 알 수 있다.
본 연구에서는 나무구조를 이용한 분류분석 방법 중 6가지의 성능을 4가지의 임상 자료를 이용하여 비교하였다. 분석 방법의 성능을 좀 더 면밀히 비교하기 위해서는 좀 더 많은 자료를 이용하여 성능을 확인하고 비교하는 작업이 이루어져야 하지만 공개되어 있는 자료를 얻기 힘든 임상 자료의 특성상 본 연구에서는 4가지의 자료만을 이용해야 하는 한계가 있었다. 또한 본 연구에서는 최근 자료 분석에 많이 이용되고 있는 R을 이용하기 위하여 R로 개발되어 있는 패키지에 국한된 연구를 진행하였다.
본 연구는 범주형 반응변수만을 다루고 있으며 이를 위한 나무구조 분류분석의 비교에 국한하였다. 향후 본 연구를 범주형 반응변수뿐 아니라 연속형 반응변수를 가지는 좀 더 다양한 형태의 임상자료로 확장하여 다양한 형태의 나무구조의 회귀모형을 살펴보고 이에 대한 성능을 비교, 분석하여 이들 방법들이 임상 자료의 형태에 따라 유용하게 이용될 수 있도록 하고자 한다.
Figure 1.
Partition of tree-structured classification tree with Iris data. 
Figure 2.
The results of various tree-structured classification trees with Parkinson
data. 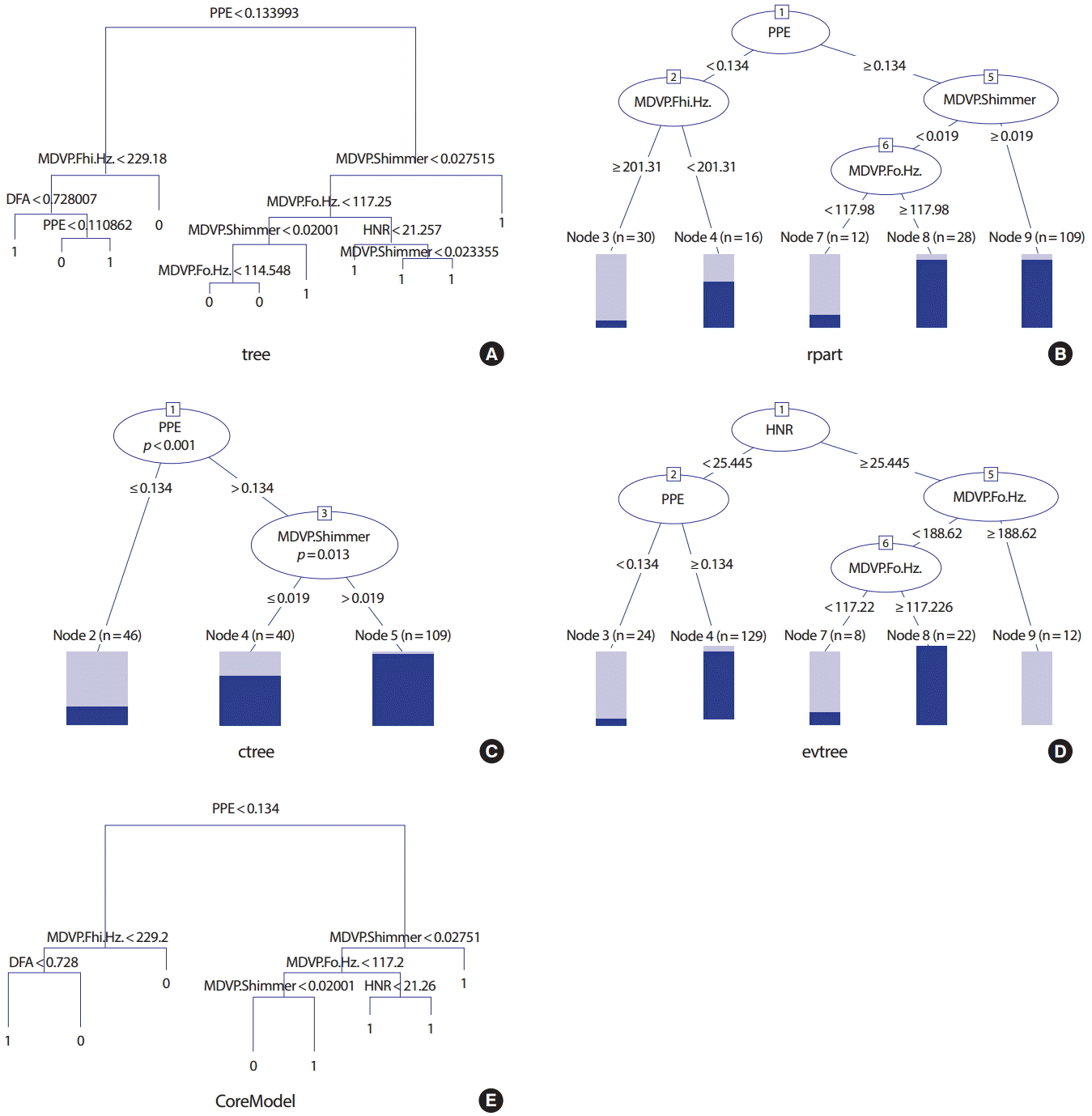
Figure 3.
Comparisons of the performance of various classification methods. 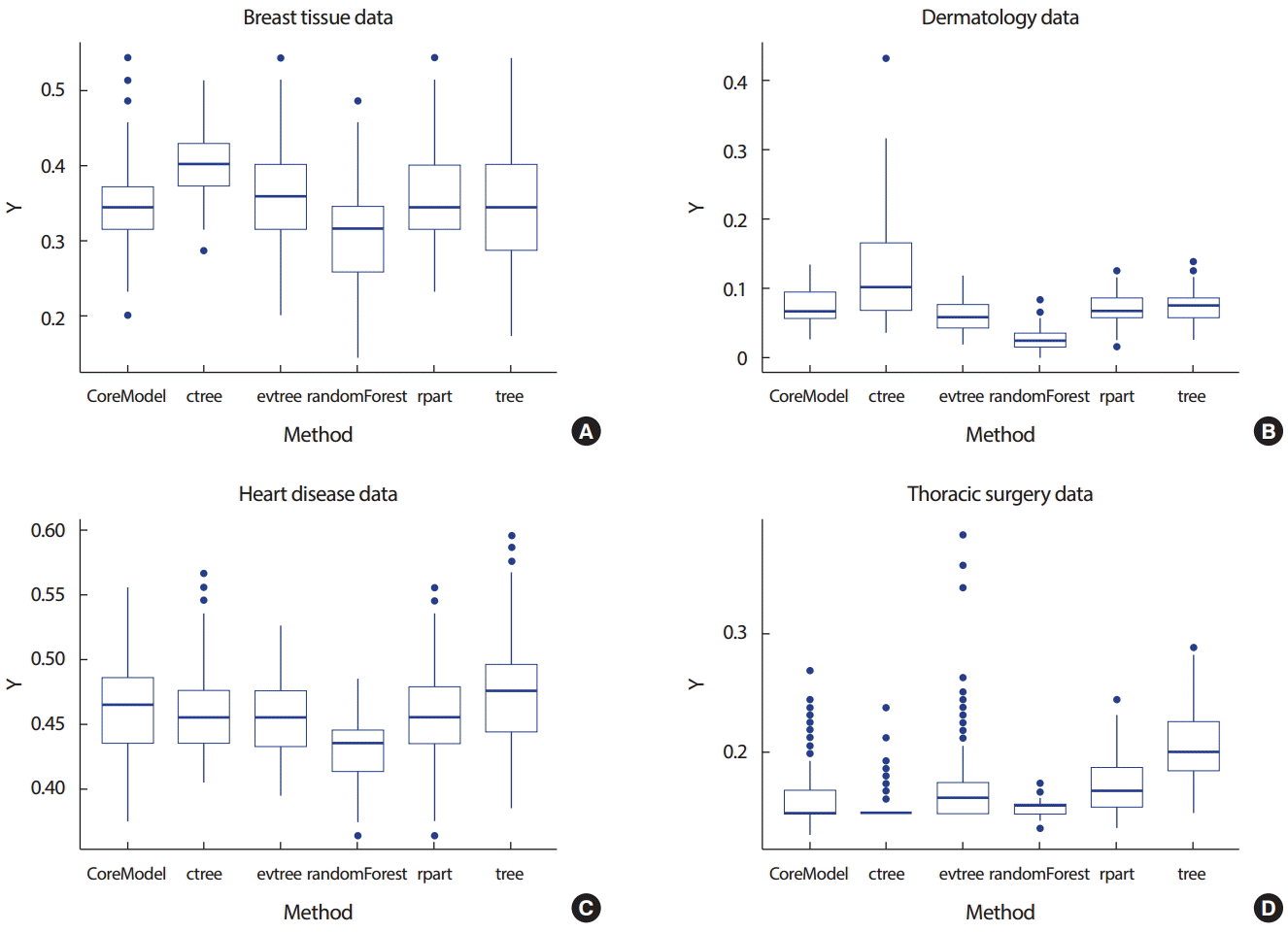
Table 1.
Variables in Parkinson data
|
Variables |
Explanation |
|
MDVP.Fo.Hz |
Average vocal fundamental frequency |
|
MDVP.Fhi.Hz |
Maximum vocal fundamental frequency |
|
MDVP.Flo.Hz |
Minimum vocal fundamental frequency |
|
MDVP.Jitter |
Measures of variation in fundamental frequency |
|
MDVP.Shimmer |
Measures of variation in amplitude |
|
NHR |
Measures of ratio of noise to tonal components in the voice 1 |
|
HNR |
Measures of ratio of noise to tonal components in the voice 2 |
|
DFA |
Signal fractal scaling exponent |
|
PPE |
Nonlinear measure of fundamental frequency variation |
Table 2.
Summaries of clinical data
|
# of variables |
# of obs. |
Categories of response variable |
|
Breast tissue data |
9 |
106 |
Tissue samples |
|
|
|
Carcinoma (21) |
|
|
|
Fibro adenoma (15) |
|
|
|
Mastopathy (18) |
|
|
|
Glandular (16) |
|
|
|
Connective (14) |
|
|
|
Adipose (22) |
|
Dermatology data |
34 |
358 |
Dermatologic disease |
|
|
|
Psoriasis (111) |
|
|
|
Seborrheic dermatitis (60) |
|
|
|
Lichen planus (71) |
|
|
|
Pityriasis rosea (71) |
|
|
|
Chronic dermatitis (46) |
|
|
|
Pityriasis rubra pilaris (20) |
|
Heart diseases data |
13 |
297 |
Level of heart disease |
|
|
|
0 (160) |
|
|
|
1 (54) |
|
|
|
2 (35) |
|
|
|
3 (35) |
|
|
|
4 (13) |
|
Thoracic surgery data |
16 |
470 |
1 year survival |
|
|
|
Alive (70) |
|
|
|
Dead (400) |
Table 3.
Results of training data set
|
Breast tissue data
|
Dermatology data
|
Heart disease data
|
Thoracic surgery data
|
|
Mean |
SD |
Mean |
SD |
Mean |
SD |
Mean |
SD |
|
tree |
0.154 |
0.030 |
0.035 |
0.010 |
0.265 |
0.020 |
0.117 |
0.013 |
|
rpart |
0.193 |
0.034 |
0.041 |
0.008 |
0.312 |
0.016 |
0.139 |
0.009 |
|
ctree |
0.311 |
0.046 |
0.119 |
0.092 |
0.397 |
0.017 |
0.149 |
0.002 |
|
evtree |
0.169 |
0.026 |
0.030 |
0.009 |
0.319 |
0.016 |
0.157 |
0.034 |
|
CoreModel |
0.191 |
0.048 |
0.040 |
0.012 |
0.320 |
0.026 |
0.141 |
0.011 |
|
randomForest |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.011 |
0.005 |
Table 4.
|
Breast tissue data
|
Dermatology data
|
Heart disease data
|
Thoracic surgery data
|
|
Mean |
SD |
Mean |
SD |
Mean |
SD |
Mean |
SD |
|
tree |
0.345 |
0.069 |
0.073 |
0.022 |
0.473 |
0.042 |
0.204 |
0.029 |
|
rpart |
0.353 |
0.055 |
0.068 |
0.018 |
0.457 |
0.035 |
0.171 |
0.022 |
|
ctree |
0.401 |
0.044 |
0.131 |
0.086 |
0.460 |
0.030 |
0.153 |
0.013 |
|
evtree |
0.355 |
0.060 |
0.061 |
0.021 |
0.454 |
0.030 |
0.169 |
0.034 |
|
CoreModel |
0.349 |
0.061 |
0.072 |
0.023 |
0.464 |
0.034 |
0.162 |
0.023 |
|
randomForest |
0.312 |
0.062 |
0.026 |
0.012 |
0.430 |
0.025 |
0.153 |
0.007 |
Table 5.
Results of one-way analysis of variance and Tukey’s HSD
|
F
|
p-value |
Tukey’s HSD result |
|
Breast tissue |
46.338 |
< 0.0001 |
(randomForest), (tree, CoreModel, rpart, evtree), (ctree) |
|
Dermatology |
149.520 |
< 0.0001 |
(randomForest), (evtree, rpart, CoreModel, tree), (ctree) |
|
Heart disease |
37.763 |
< 0.0001 |
(randomForest), (evtree, rpart, ctree, CoreModel, tree) |
|
Thoracic surgery |
132.310 |
< 0.0001 |
(randomForest, ctree), (CoreModel), (evtree, rpart), (tree) |
Table 6.
Breast tissue data: mean of sensitivities and specificities in test data sets
|
Adipose
|
Carcinoma
|
Connective
|
Fibro adenoma
|
Glandular
|
Mastopathy
|
|
Sensitivity |
Specificity |
Sensitivity |
Specificity |
Sensitivity |
Specificity |
Sensitivity |
Specificity |
Sensitivity |
Specificity |
Sensitivity |
Specificity |
|
tree |
0.91 |
0.59 |
0.82 |
0.61 |
0.86 |
0.62 |
0.33 |
0.71 |
0.56 |
0.67 |
0.35 |
0.72 |
|
rpart |
0.95 |
0.06 |
0.79 |
0.22 |
0.78 |
0.22 |
0.35 |
0.65 |
0.61 |
0.39 |
0.30 |
0.70 |
|
ctree |
0.97 |
0.03 |
0.75 |
0.25 |
0.76 |
0.24 |
0.07 |
0.93 |
0.60 |
0.40 |
0.30 |
0.70 |
|
evtree |
0.92 |
0.58 |
0.83 |
0.60 |
0.79 |
0.62 |
0.33 |
0.70 |
0.61 |
0.65 |
0.29 |
0.72 |
|
CoreModel |
0.91 |
0.58 |
0.84 |
0.60 |
0.86 |
0.62 |
0.24 |
0.72 |
0.65 |
0.65 |
0.28 |
0.73 |
|
randomForest |
0.94 |
0.63 |
0.85 |
0.65 |
0.82 |
0.67 |
0.42 |
0.73 |
0.66 |
0.69 |
0.35 |
0.76 |
Table 7.
Dermatology data: mean of sensitivities and specificities in test data sets
|
Psoriasis
|
Seborrheic dermatitis
|
Lichen planus
|
Pityriasis rosea
|
Chronic dermatitis
|
Ppityriasis rubra pilaris
|
|
Sensitivity |
Specificity |
Sensitivity |
Specificity |
Sensitivity |
Specificity |
Sensitivity |
Specificity |
Sensitivity |
Specificity |
Sensitivity |
Specificity |
|
tree |
0.97 |
0.91 |
0.90 |
0.93 |
0.97 |
0.92 |
0.82 |
0.94 |
0.96 |
0.92 |
0.82 |
0.93 |
|
rpart |
0.96 |
0.04 |
0.94 |
0.07 |
0.96 |
0.05 |
0.80 |
0.20 |
0.99 |
0.01 |
0.84 |
0.16 |
|
ctree |
0.96 |
0.04 |
0.86 |
0.15 |
1.00 |
0.01 |
0.47 |
0.54 |
0.82 |
0.18 |
0.98 |
0.02 |
|
evtree |
0.96 |
0.93 |
0.93 |
0.94 |
0.96 |
0.93 |
0.84 |
0.96 |
0.99 |
0.93 |
0.92 |
0.94 |
|
CoreModel |
0.98 |
0.91 |
0.92 |
0.93 |
0.97 |
0.92 |
0.81 |
0.95 |
0.93 |
0.93 |
0.82 |
0.93 |
|
randomForest |
1.00 |
0.96 |
0.94 |
0.98 |
1.00 |
0.97 |
0.90 |
0.99 |
1.00 |
0.97 |
0.97 |
0.97 |
Table 8.
Heart diseases data: mean of sensitivities and specificities in test data
|
0
|
1
|
2
|
3
|
4
|
|
Sensitivity |
Specificity |
Sensitivity |
Specificity |
Sensitivity |
Specificity |
Sensitivity |
Specificity |
Sensitivity |
Specificity |
|
tree |
0.83 |
0.18 |
0.16 |
0.61 |
0.23 |
0.57 |
0.21 |
0.57 |
0.09 |
0.55 |
|
rpart |
0.86 |
0.14 |
0.18 |
0.82 |
0.22 |
0.78 |
0.19 |
0.81 |
0.04 |
0.96 |
|
ctree |
0.89 |
0.11 |
0.07 |
0.93 |
0.21 |
0.79 |
0.18 |
0.81 |
0.00 |
1.00 |
|
evtree |
0.89 |
0.15 |
0.12 |
0.64 |
0.19 |
0.60 |
0.22 |
0.59 |
0.01 |
0.57 |
|
CoreModel |
0.87 |
0.15 |
0.11 |
0.63 |
0.23 |
0.58 |
0.17 |
0.59 |
0.04 |
0.56 |
|
randomForest |
0.94 |
0.15 |
0.09 |
0.68 |
0.25 |
0.61 |
0.17 |
0.63 |
0.02 |
0.59 |
Table 9.
Thoracic surgery data: mean of sensitivities and specificities in test data
|
Alive
|
Dead
|
|
Sensitivity |
Specificity |
Sensitivity |
Specificity |
|
tree |
0.12 |
0.91 |
0.91 |
0.12 |
|
rpart |
0.06 |
0.94 |
0.96 |
0.04 |
|
ctree |
0.01 |
0.99 |
0.99 |
0.01 |
|
evtree |
0.03 |
0.97 |
0.97 |
0.03 |
|
CoreModel |
0.03 |
0.98 |
0.98 |
0.03 |
|
randomForest |
0.01 |
0.99 |
0.99 |
0.01 |
REFERENCES
1. Morgan JN, Sonquist JA. Problems in the analysis of survey data, and a proposal. J Am Stat Assoc 1963;58(302):415-434.  2. Messenger R, Mandell L. A modal search technique for predictive nominal scale multivariate analysis. J Am Stat Assoc 1972;67(340):768-772.  3. Quinlan JR. Induction of decision trees. Machine learning 1986;1(1):81-106.  4. Breiman L, Friedman J, Stone CJ, Olshen RA. Classification and regression trees. Boca Raton, FL: CRC press; 1984.
5. Kass GV. An exploratory technique for investigating large quantities of categorical data. Applied Stat 1980;29(2):119-127.  6. Loh WY, Vanichsetakul N. Tree-structured classification via generalized discriminant analysis. J Am Stat Assoc 1988;83(403):715-725.  7. Quinlan JR. C4. 5: programs for machine learning. Elsevier; 1993.
8. Loh WY, Shih YS. Split selection methods for classification trees. Stat Sinica 1997;7:815-840.
9. Kim H, Loh WY. Classification trees with unbiased multiway splits. J Am Stat Assoc 2001;96:598-604.  10. Hothorn T, Hornik K, Zeileis A. Unbiased recursive partitioning: a conditional inference framework. J Compu Graph Stat 2006;15(3):651-674.  11. Grubinger T, Zeileis A, Pfeiffer KP. evtree: evolutionary learning of globally optimal classification and regression trees in R. No. 2011-20. Working Papers in Economics and Statistics; 2011.
12. Robnik S. CORE-a system that predicts continuous variables. Proceedings of Electrotechnical and Computer Science Conference (ERK’97), Portoroz, Slovenia. Ljubljana: Slovene Section of IEEE. 1997.
14. Robnik SM, Kononenko I. An adaptation of Relief for attribute estimation in regression. InMachine Learning: Proceedings of the Fourteenth International Conference (ICML). San Francisco, CA: Morgan Kaufmann Publishers Inc. 1997;296-304.
15. Li M, Vitányi P. An introduction to Kolmogorov complexity and its applications. New York, NY: Springer Science & Business Media; 2013.
16. Breiman L. Random forests. Machine Learn 2001;45(1):5-32. 
|
|














