AbstractObjectivesMain objective of this study was to estimate crematory facility demand of Suwon city, using Seasonal ARIMA Model. This study aims to estimate the demand based on the number of currently operating crematory facilities, dividing into inward district and outward district of Suwon city.
MethodsAs the construction of crematory facilities is greatly in need of supply along with the increasing funerals, it requests more accurate estimation of the demand in specific area. This study employed Seasonal ARIMA Model which is useful to deal with time series data with small size and various patterns, instead of the Gompertz curve and logistic curve frequently used in the past. This study did analyses in four steps, discrimination of stationarity (balance for average and dispersion), identification of functions (ACF, PACF), model diagnostic (estimation of parameter), and decision (forecasting of crematory facilities).
ResultsFirst, the demand of cremation in inward district of Suwon was estimated to be 4,051 persons in 2017 and to be 5,129 persons in 2022 using the ARIMA (0,1,1)(1,1,0)S=12 Model, which is to be increased 31.8 percent points compared to that of 2016. Second, the demand of cremation in outward district of Suwon was estimated to be 6,731 persons in 2017 and 7,060 persons in 2022 using the ARIMA (0,0,3)(1,1,1)S=12 Model. Altogether the users of crematory facilities were estimated to be 10,782 persons in 2017 and 12,189 persons in 2022, which shows increasing trend of 3 to 4 percent points every year.
ConclusionsThis study proved that Seasonal ARIMA Model is a proper tools to estimate the crematory facility demand in specific area. Demand and supply of crematory facilities should be estimated based on reliable statistics and data. Suwon city should provide more facilities to meet the increasing need of cremation. For this, Suwon city should input more investment for improving of quality of facilities and coordination of the number.
서론장사시설은 타 시설보다 사전 투자규모가 비교적 크고 비선호시설로 인식되어 주민들의 반대로 입지와 건립이 쉽지 않다. 비선호시설이란 사회 전체적 또는 국가적 차원에서는 필요성이, 개인적 또는 지역적 차원에서는 해악성이 강하게 부각되는 양면성을 동시에 지닌 시설을 말한다[1]. 즉, 대부분의 장사시설은 공공성을 근간으로 하는 공익시설들로서 일반적인 시장원리에 따라 적정한 공급이 이루어지기 현실적으로 어렵다. 특히 화장시설은 더욱 그러한 실정이며, 주로 정부 차원의 직·간접적인 개입에 의해 공급이 이뤄져 왔다. 사실 화장시설의 입지는 형평성 문제를 유발시켰고, 입지로 인한 부정적으로 예측되는 결과-예를 들면 지가하락, 환경오염, 지역적 오염, 교통 혼잡, 교육환경의 훼손 등-를 원천적으로 차단함으로써 지역이익을 보호하고자 하는 지역사회와 장사시설의 입지를 통해 전체사회의 삶의 질을 높이는 등 공익을 구현하고자 하는 사업추진자들 간에 대립과 마찰이 빈번이 일어났다. 그 결과, 2017년 현재까지 전국의 화장시설은 공설로만 운영되고 개수도 60개소1) 뿐이며, 많은 지역의 주민들은 타 지역에 설치된 화장시설을 이용할 수밖에 없다.
그렇기 때문에 장기적인 측면에서 정부기관을 비롯한 장사관련 기관은 정책수립 및 사업수행에 앞서 충분한 수요조사와 신뢰할 수 있는 수요예측을 바탕으로 정책 및 전략을 수립해야 한다. 수요예측은 해당 시설 공급 및 수요를 현재 시점에서부터 과거 데이터나 정보를 통해 향후 미래를 예측하거나 또는 과거와 현재의 시설 수급과 그에 따른 영향요인을 근거로 불확실한 미래의 공급과 수요를 추정하는 것을 의미한다. 이러한 예측결과는 수요분석을 기초로 그에 따른 각종 예측조사의 결과를 종합하여 미래의 수요를 계량화한다.
기존 장사시설 수요예측 연구에서는 초기발전단계, 중간확산단계, 최종포화단계로 성장형태를 보인다. 이때 이를 설명하는 방법으로서 콤페르츠 곡선(Gompertz curve)이나 로지스틱 곡선(logistic curve)을 사용하였다. 이 방법의 핵심은 바로 최종포화단계에서의 크기를 주로 관찰치를 시간에 따라서 각 곡선의 모수를 찾아내는 것이다. 하지만 현재의 장사시설의 예측은 초기 산업의 발전단계가 아닌 많은 발전을 성과를 이룬 상태–대표적으로 화장률의 경우 1994년에는 20.5%이었고, 2001년은 38.5%, 2015년은 80.8%–이기 때문에 이제는 보다 정확도가 높은 장래 수요예측으로 특히 화장시설 특성에 맞는 최적 모형 개발이 필요하다. 이러한 이유로 적은 자료양과 다양한 패턴을 가진 시계열 자료에도 적용 가능한 ARIMA 모형을 제안한다. 최근의 관측값이 미래의 예측력에 영향력이 크다는 개념으로 출발하여 자기회귀 모형(autoregressive model, AR)과 이동평균 모형(moving average, MA)이 결합한 형태를 말한다.
따라서 본 연구에서는 ARIMA 모형을 이용하여 최대 수요 기준으로 수요를 추정하는 것으로 목적으로 하며, 수원시에서 운영하고 있는 화장시설을 중심으로 유족을 관내·외로 구분하여 추정을 하였다. 이를 위해서 기간은 2022년까지 하도록 하며, 공급에 대한 예측은 현재 공급된 시설을 효율적으로 이용하는 것으로 가정, 더 이상의 공급은 없는 것으로 가정하였다.
ARIMA 모형은 다양한 관측치를 이용할 수 있고 특정사건이나 수요의 구조적 측정, 외부 충격이 가능한 다변량 시계열 예측모형이며, 시계열모형의 단점인 수요의 구조적 측정과 영향력 측정의 부재라는 단점을 극복하기 위한 모형이라 할 수 있어, 그 가치가 높다[2].
이론적 배경수요예측수요예측에 사용하는 모형은 크게 정성적 모형과 정량적 모형, 그리고 두 가지 이상의 모형을 복합 적용하는 결합 모형으로 나눌 수 있다. 그리고 수요예측에 사용되는 모형은 다양하고 동일한 자료로 예측모형이나 사용되는 변수에 따라 다른 결과로 예측될 수 있기 때문에 모형의 특성을 이해하고 예측 대상과 목적에 맞는 모형을 찾는 것이 중요하다(Table 1).
우선, 정성적 모형은 중장기적 예측에 적합하며, 일반적으로 예측기법의 적용에 소요되는 비용과 시간이 높은 편이고 연구자의 주관이나 판단 또는 여러 사람들의 의견을 종합하여 수요를 예측하는 모형이다. 그렇기 때문에 과거 자료가 부족할 때 사용할 수 있으며, 직관적인 전문가적 식견 반영이 가능하다. 반면 연구자의 주관적인 개입이 가능하며, 정책적인 의지로 외부의 주관적 환경 반영으로 왜곡된 결과가 나타날 수 있다.
정량적 모형은 수집된 과거자료를 바탕으로 통계적 또는 계량적으로 미래수요를 예측하는 방법이다. 즉, 과거 자료를 통하여 과거의 변화와 동향을 파악하고 변수 간의 관계를 규명하는 등의 방법으로 예측하는 모형이다. 이런 모형은 추세분형이 있는데 과거 추세가 계속 지속된다는 가정에 따라 과거의 패턴을 분석하기 위한 형태에 적합한 함수형태를 적용하는 모형이다. 이는 비교적 간단하게 분석이 가능하지만 과거의 조건들이 변화 없다는 가정 때문에 이후 환경변화의 반영이 어렵다. 이러한 모형의 대표적인 분석 방법은 콤페르츠 모형(Gmpertz model)2)과 로지스틱 모형3)이 있다. 과거 대부분 관련 선행연구[3-6]4)는 이런 추세분석법을 이용하여 수요예측을 시행하였다. 즉, 장사시설의 수급분석을 위해서 인구수와 사망률 등 인구통계학적 조건과 지역주민들의 장사방법과 장사시설 선호도 등을 파악했다. 다음으로 수요추계의 경우 사망자 추계와 인구 추계를 실시하고 화장률에 관한 추계 실시와 이후 대상자별 유형에 따른 장사시설에 관한 추계를 각각 실시하였다. 반면, 장사시설 공급추계의 경우 기본적인 기존 시설의 분석을 통하여 화장장과 봉안시설 및 자연장 등에 대한 기초적인 분석을 실시하고 향후 수원시 계획 등을 고려하여 공급을 추계하였다. 마지막으로 수요와 공급을 추계한 결과를 토대로 장사시설 수급계획을 실시하고, 이를 검증하였다.
ARIMA 모형ARIMA 모형은 Auto Regressive Integrated Moving Average 모형의 축약어이다. 중요한 것은 ARMA 모형(Auto Regressive Moving Average)5) 인데, 일반적인 시계열 자료에 자기상관이 존재하고 이러한 효과가 지속적으로 나타나는 특징을 갖고 있으며, 이러한 패턴을 반영하기위해 사용하는 모델 중 하나이다. 종속변수의 직접적으로 과거 값에 의존하는 부문(AR)과 직접적으로 과거 데이터에 무작위로 발생한 교란요인에 영향을 받는 부문(MA)을 반영하여 설명력을 높여주는 모형이다.
Box and Jenkins [8]는 ARIMA 모형의 이점6)으로서 간결성(parsimony)을 제시하였는데 이는 가능한 최소의 추정 파라미터 사용하고 적정한 차수의 아카이케정보기준(Akaike Information Criterion, AIC)을 사용한다. 사실 시계열이 가지는 특징은 불충분한 자료의 수, 외부잡음(white noise)의 상당한 개입, 일정 시간간격이 아닌 자료수집, 비정상성을 가지는 경우가 많아 시계열분석과 예측을 근본적으로 어렵게 만드는 요인이 된다[9]. 또한, ARIMA 모형은 단기예측에 주로 사용되는데 이는 ARIMA 모형은 먼 과거보다는 최근 시점에 가까운 과거 관측값에 더 많은 비중을 주기 때문이다. 최근 시점에 가까운 과거에 비중을 더 준다는 것은 AIRMA 모형에 근거하여 얻어진 장기 예측값이 단기 예측값에 비해 신뢰성이 적기 때문이다[10].
연구 방법연구모형
Figure 1에 제시한 바와 같이, 예측 시 사용되는 관측데이터가 비정상적시계열(추세를 가짐)이고, 계절성을 갖고(패턴을 가짐) 있기 때문에 ARIMA 모형을 적용하여 개념적 연구모형을 설계하였다.
예측 범위 및 데이터 수집본 연구의 수요는 수원시 화장시설인 연화장의 이용률에 대한 것이며, 예측범위는 2017년 7월부터 2022년 12월까지 66개월로 예측하였다. ARIMA 모형을 설정하기 위한 표본의 크기에 대하여 “ARIMA 모형을 설정하기 위해서는 적절한 표본의 크기가 필요한데 Box and Jenkins는 최소 50개 이상의 관측값이 필요하다고 하였으며 Jung은 추세를 고려하지 않고 최대한 많은 데이터를 수집과 이용”이 필요하다[10,11].
이에 따라서 수원시 장사시설의 화장시설에 대한 수요예측 시 사용되는 데이터는 2001년 1월부터 2016년 12월까지 월별 데이터를 사용하였다. 즉, 실제 관측값의 수는 192개이다(Table 2).
자료 분석본 연구는 수집된 자료를 SPSS 21.0 프로그램(SPSS Inc., Chicago, IL, USA)을 사용하여 분석하였다. 그리고 사용된 관측데이터를 연구모형의 단계에 따라 분석하였다. 우선, 정상성(stationarity)을 알아보기 위하여 주어진 관측데이터에 대하여 시계열자료의 정상성을 만족해야한다. 일반적으로 정상성이란 데이터의 일정한 주기로 나누었을 때, 각 주기에 해당하는 평균과 분산이 일정한 것을 의미한다. 이때 분산과 평균이 비정상적일 경우 정상성을 만족시키기 위해서 각각 변수 차분과 변화 등으로 이를 만족시켜야 한다[10]. 또한 분산이 비정상적인 계열로 나타나면 보통 자연로그를 취하게 되면 정상성이 회복된다. 그렇지 않을 경우 평균의 정상성을 위하여 차분을 수행하게 되는데 1차 차분은 자주 사용한다.
다음으로 모형에 대하여 식별은 두 개의 이론적 상관함수인 자기상관함수(auto correlation function, ACF)와 편자기상관함수(partial auto correlation function, PACF)를 이용하여 추정된 ACF와 PACF가 두 개의 이론적 상관함수와 각각 일치하는지를 비교하게 된다. 이 단계는 관측값들 사이에 존재하는 상관관계를 측정하여 ARIMA (p,d,q) 모형을 구성하는 자기회귀(AR) 요소인 p와 이동평균(MA) 요소인 p를 선택하는 단계로, ACF와 PACF의 형태에 따라 모형을 식별하게 된다.
그리고 추정단계의 경우 앞서 고려한 모형의 계수를 추정하고, 모수가 통계적으로 유의한지를 판단하게 된다. 그리고 파라미터를 추정하고, 시계열 자료가 그 모형에 얼마나 잘 적합되는지를 진단한다. 또한 적합도가 좋은 모형 측정하는 통계량인 R2와 정상 R2가 있는데, 시계열 자료가 특정적인 추세가 있거나 분산을 정상적으로 만들기 위해 변수변환을 실시했다면 정상화 R2 사용을 한다.
마지막으로 모형진단에서는 모형의 적합성을 점검하게 된다. 이때 통계적으로 적절한 모형인지는 백색잡음(white noise)7)들이 서로 독립(즉, 자기상관되어 있지 않음)이어야 하며, 이를 검증하기 위해 Box와 Ljung의 통계량값 및 이상값 수를 확인하게 된다.
연구 결과정상성 및 계절성 점검본 연구에서 수집된 관측데이터의 정상성을 판단하기 위하여 시퀀스차트를(순차도표) 분석하였고, 그 결과 비정상성이 파악되었다. 이뿐만 아니라 2006년도와 2013년도에 아웃라이어(outlier)인 이상치가 발생하였다. 즉, 2006년도와 2013년도에 화장률이 급증한 이유는 윤달로 일반적인 시체가 아닌 개장유골을 통계상 잡힌 것으로 관계자의 말이 있었다. 이런 경우 시계열 분석의 흐름상 일시적인 이용률 급증으로 판단되어 보정하였다. 보통 보정은 보편적인 것이 아닌 특정 이상으로 판정되었을 때 그 영향력을 줄이기 위해서 사용하게 되는데, 이상점으로 판정된 자료의 가중치는 모두 1이 되도록 하고 이상점이 아닌 자료의 가중치에 의해서 보정되지만 이상점인 자료와 이상점이 아닌 자료에 따라 조금씩 다르다(Figure 2).
순차도표 분석 결과, 관내 화장장 이용의 수요는 2001년부터 2016년까지 월 평균 0.9%, 연 평균 11.3%로 증가 추세였다. 그리고 이러한 관내 수요는 보통 3년마다 있는 윤달에 맞춰 평소 2-3배 증가하기도 하였다. 이렇듯 관내 화장장 이용 실적은 전반적으로 평균이 증가하는 추세이긴 하나 분산 또한 전체 수준이 커지기 때문에 평균과 분산이 모두 비정상적이라 할 수 있다. 이렇듯 시계열 자료와 같이 분산이 비정상적이면서 평균 또한 비정상적일 경우 변수변환을 사용하여 분산을 정상적으로 만든 후 그 다음 차분을 통해 평균을 정상적으로 만들어야 한다. 왜냐하면 자료를 먼저 차분하게 되면, 가끔 부호가 음인 값이 산출되어 자연로그를 취한 값을 계산할 수 없기 때문이다[10]. 이에 따라 관내 화장장 수요 데이터를 자연로그 변환한 후 1차 차분한 결과는 Figure 3과 같다.
그 결과 Figure 3의 그래프를 보면 분산과 평균 모두 정상성을 만족한 것을 알 수 있다. 즉, 관내 화장장 수요를 예측하기 위해서는 로그변환, 계절차분, 1차 차분을 수행하여 데이터의 정상성이 마련되었다고할 수 있다.
모형 식별모형 식별을 위해 앞서 자연로그변환, 계절차분, 1차 차분된 관내 화장장 이용률에 대한 데이터의 ACF 및 PACF를 살펴보면 아래와 같다. 우선 ACF에서 ACF(1), ACF(12)에서 크게 스파이크가 발생한다. 그러나 대부분 값들이 신뢰한계선 안에 있다. 반면 PACF(1), PACF(12), PACF(36)에서 크게 스파이크가 발생하였지만 ARIMA(0,1,1)(1,1,0) S =12로 식별하였다(Figure 4).
모형 진단 및 예측결과모형진단은 추정된 모형에 대하여 통계적으로 적합한지를 판단하는 단계인데, 이때 자기상관함수와 검증 통계량을 통하여 이를 검증하게 된다. 우선, 수원시 연화장의 관내이용자 수요에 대한 ARIMA 모형의 통계량은 Table 5와 같으며 ARIMA(0,1,1)(1,1,0)S =12 모형의 Ljung-Box Q(18)란의 유의확률값인 0.544로 유의수준 5%보다 월등히 크기때문에 백색잡음항이 독립이며, 귀무가설을 채택할 수 있게 된다.
관외이용자의 수요예측 결과앞서 관내 화장장 수요예측과 같은 방법으로 관외이용률 모형의 추정, 진단 및 예측하였다. 그 결과는 다음과 같은데, 식별된 모형인 ARIMA(0,0,3)(1,1,1)S =12의 결과값은 Table 7과 같다. 이때 상수항 유의수준 값이 0.05 이상이므로 제외하도록 하고 재분석을 실시하였고, 그 결과로서 추정된 계수들의 유의수준이 모두 0.05 이하로 매우 유의하게 나타났다.
그리고 ARIMA 모형의 통계량은 Table 8과 같으며 ARIMA(0,0,3) (1,1,1)S =12 모형의 Ljung-Box Q(18)란의 유의확률 값인 0.071로 유의수준 5%보다 크기 때문에 백색잡음항이 독립이며, 귀무가설을 채택할 수 있게 된다. 분석과정에서 이상치 8개(2002년 1월, 3월, 6월과 2006년 9월, 2013년 2월과 7월)가 발생하여 이에 대한 이상점 보정을 실시하였다.
2017년 관외이용자 수요는 6,731명으로 예측되었고, 2022년에 관외 이용자 수요는 7,060명으로 예측되었다(Table 9).
이를 종합해 수원시 연화장의 이용자 수요는 Table 10과 같이 나타났다. 향후 2020년에 화성시가 직접 운영하는 공설 화장장이 운영 될 경우 수요에 대한 변화가 예상되고, 수원시 연화장 이용자 수요에 감소가 예상되지만 본 연구에서 논외로 하기로 한다. 이에 따라 2017년 화장장 이용자수는 10,782명으로 예측되며, 매년 약 3-4%씩 증가 추세를 보일 것으로 예측되었다. 그리고 2022년에는 12,189명이 이용할 것으로 예측된다.
결론 및 제언이상의 연구 결과를 종합해 보면, 먼저 수원시 관내 화장장 이용의 수요는 2001년부터 2016년까지 월평균 0.9%, 연평균 11.3%로 증가 추세였다. 그리고 이러한 관내 수요는 보통 4년마다 있는 윤달에 맞춰 평소 2-3배 증가하기도 하였다. 관외 화장장 수요에 대한 예측을 종합적으로 판단한 결과 수원시 화장장의 수요예측은 2017년 4,051명에서 2020년 4,659명으로, 2022년에는 5,129명으로 증가하는 것으로 추계되었다. 관내 화장장 수요예측과 같은 방법으로 관외 화장장 이용률 모형의 추정과 예측 결과 2017년 관외 화장장 수요는 6,731명으로 예측되었고, 2022년에 관외 화장장 수요는 7,060명으로 예측되었다.
이와 같이 수원시 화장장 수요는 지속적으로 증가하는 것으로 나타나고 있으므로 수급추계를 근거로 수원시 중장기 수급계획의 기본방향을 설정할 필요가 있다. 수원시 수급계획의 기본방향은 증가하는 화장장 수요에 대비하여 장사시설의 양적 확충과 질적 개선을 모색하도록 한다. 화장시설 운영의 기본 원칙과 새로운 패라다임을 정립하고, 효율적인 제도와 첨단 관리시스템을 도입하여 화장시설의 효율성을 제고하여야 한다.
이상의 장사시설 수급추계 논의의 결과는 장사시설에 관한 체계적인 정보제공과 장사시설에 관한 종합적인 시설 구축과 시스템 운영에 기여할 수 있다. 체계적인 장사시설에 관한 통계는 장사시설을 계획적으로 공급하여 수급을 균형화시킴으로써 사후복지수준을 향상시키며, 무분별한 장사시설 설치로 인한 자연환경 훼손을 방지할 수 있다. 향후 화장률에 따른 화장시설과 화장 후 이용하는 시설을 포함한 봉안시설, 자연장 시설의 공급과 확충 정책에 기초자료로 활용되며, 수원시 장사시설 수급에 관한 기초적인 정책방안에 활용될 수 있다.
첫째, 장사시설 수급정책은 통계적 자료를 근거로 정책방향을 설정해 둘 필요가 있다. 장사시설설치의 여러 문제점과 현실적인 한계가 있음에도 불구하고 기본이 되는 장사정책이 흔들리면 바람직한 장사문화 발전 정착이 어렵다.
둘째, 수원시 장사시설에 이용에 대한 적절한 조정이 필요하며, 장사시설 개선에는 적정한 투자가 필요하다. 장사시설은 누구나 이용하는 것이 원칙이지만 현재 시스템으로는 주인인 수원시민이 화장시설의 이용의 상대적 차별이 일어날 수 있으므로 제도적 조정이 필요한 것으로 판단된다. 또한 추모시설의 수급을 위해서는 사용자의 자격과 사용기간 및 만료 시 후속조치, 사용료 등을 종합적으로 개선하여야 한다.
셋째, 장사시설 수요에 대비하는 신규 장사시설 도입을 적극 검토해야 한다. 장사시설에 대한 수요는 양적인 측면에서 증가할 뿐만 아니라 질적인 면에서 개선이 요구된다. 장사시설 수요자 중심에 입각하여 개성의 다양성, 차별성을 고려한 장사시설 인프라 구축과 기존 시설의 경제적, 효율적 활용 방안을 모색하여야 한다. 저출산, 핵가족, 고령화라는 선진국들의 공통된 사회변화에 따라 새로이 등장한 장법과 시설은 대체로 “저비용”, “공동 사용”과 “영구 보존”에 초점이 맞춰져 있다고볼 수 있다. 수원시의 여건상 새로운 추모시설 공간 입지가 어렵기 때문에 기존 시설을 활용한 품격 있는 장사시설 도입에 대해 전향적인 검토가 필요하다.
장사시설에 대한 수급추계에 대한 분석결과 화장시설과 자연장에 대한 수요는 더욱 증대할 것으로 예상된다. 장사시설의 부족문제를 해결하기 위해서는 인접 지방자치단체와의 상호이해를 통해 장사시설의 공동설치 방안을 마련하는 데 유용하게 활용될 수 있을 것으로 판단된다. 현재 우리나라는 고령화에 따른 사망자 수 증가로 장사시설의 수요는 증가하고 있다. 화장시설은 여전히 비선호시설로서 시설 확충과 정비를 둘러싼 갈등이 내재되어 있으므로, 수원시는 화장장 수요에 맞춰 화장시설을 적기에 공급하고 바람직한 장사환경을 조성할 필요가 있다. 수원시 장사시설에 대한 지역 주민들의 욕구가 다양화되면서 당면한 과제인 장사시설 등에 대한 분석과 수급추계 결과에 따라 장사시설의 확충 및 정비작업이 필요하다.
연구의 한계점 및 보완과제로서 수원시의 장사시설의 수요추계는 경기도 전체 또는 전체의 장사시설 수요와 공급의 상당한 영향관계에 있으며, 현실과 달리 화장시설을 이용하는 유족들의 지역 간 이동 수요를 충분하게 검토해야 하지만 본 연구에서는 이를 반영하지 못하였다. 뿐만 아니라 본 연구의 사용된 변수들이 장사시설 수요에 유의한 영향을 미치는 모든 요인을 포함한 것이라고 볼 수는 없기 때문에 추후에는 좀 더 다양한 측면의 개입변수를 포함하며 정교한 수요예측 모델을 연구해야 할 것이다.
Notes1) e하늘장사정보시스템 사이트(http://www.ehaneul.go.kr)의 장사시설 현황자료 참조. 2) 이 모형은 1825년 영국의 수학자 Benjamin Gompertz에 의하여 모형이 소개되었으며, 초기 사망률을 설명하였고, 이후 장기 소득분포를 설명하는 데 자주 인용되었다. 현재에는 최초 시장에 소개된 제품이 도입기에 가파른 성장을 하다가 성장기 단계에서는 점차 그 사용이 둔화되는 과정을 나타나내는 장기예측 모형에서 많이 사용되었다. 즉, 시점 0에서 2) 콤페르츠 함수형태는 기본: 2) 시간 t 대신 독립변수들의 선형결합 형태: 3) 이 함수는 S모양의 형태를 취하며, 곡선의 변곡점에 대하여 대칭이고, 곡선의 기울기는 항상 양(positive)이다. 역시 위의 식을 직분하면 다음과 같은 함수형태가 유도된다. 3) 로지스틱의 함수형태는 기본: 4) 본 연구에서는 인구 및 사망자 추세는 그대로 인용하되, 현실성이 떨어지는 부분은 보정을 하여 사용하였다. 또한 기존 대부분 연구들은 로지스틱 분석방법을 사용하였는데, 이때 단기 예측의 한계점에 대한 미비점과 이미 높은 화장률에 기존 분석방법은 무의미할 수 있어, 이를 보완하기 위하여 단기 예측의 정확성을 확보하고, 장기적으로는 화장률에 대한 추세 분석을 실시하였다. 5) 이 모형을 장사시설 수요예측이 많이 사용하지 않아서 본 모형에 대해 장사시설 수요의 영향요인이 분석이 선행되어야지만 미실시하였다. 그러나 일반적인 경제, 사회, 정치, 환경 등 여러 가지 대외적 사건들에 영향을 받는다고 볼 수 있다. 다만, 기존 선행연구를 볼 때 경제적, 사회적 요인에 대한 민감성과 산업 자체의 수요의 불확실성은 예측의 정확성을 증폭시킨다는 점을 볼 수 있다. Figure 4.Inside crematory facilities demand data of ACF, PACF. Bar factor, Reliability upper value, Reliability lower limit value. ACF, auto correlation function; PACF, partial auto correlation function. 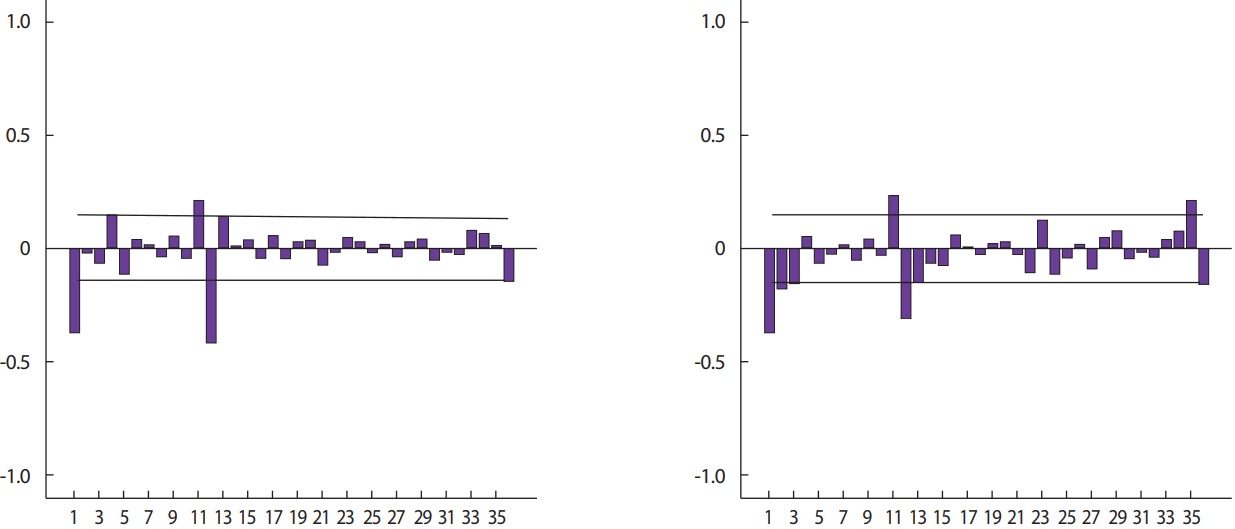
Table 1.Model items for estimation supply and demand of funeral faculty The Korea Transport Institute [7]. Table 2.Data collection and range of forecasting Table 3.Inside crematory facilities demand by ARIMA model parameter (A constant is included) Table 4.Inside crematory facilities demand by ARIMA model parameter (A constant is not included)
Table 5.Inside crematory facilities demand by ARIMA model statistic
Table 6.Short-term demand result for inside crematory facilities Table 7.Outside crematory facilities demand by ARIMA model parameter (A constant is not included) Table 8.Outside crematory facilities demand by ARIMA model statistic
Table 9.Short-term demand result for outside crematory facilities REFERENCES1. Oh CT, Yu HW. A Study on management problems and overcoming strategies according to service characteristics. Korean Public Adm Quart 1997;9(3):427-446. (Korean).
2. Kim MS, Kim GW, Park SS. A study on the air travel demand forecasting using time series ARIMA-intervention model. J Korean Soc Aeronaut Flight Operation 2012;20(1):63-74. (Korean).
3. Kim GH. The supply and demand plans and policy directions of funeral facilities in the city of Seoul. Seoul: Seoul Development Institute; 2001. (Korean).
4. Kim GH, Sun HS. The supply and demand plans and policy directions of funeral facilities in the city of Seoul. Seoul: Seoul Development Institute; 2007. (Korean).
5. Lee PD, Kim HW, Kim SB. Analysis of preference factors on the funeral facilities: focusing on residents in Gyeonggi province. J Consumer Policy Stud 2015;6(2):87-106. (Korean).
6. Park BS, Park TH, Kim DH, Lee PD, Park WJ, Jung CJ, et al. A study on status survey and improvement plans in Suwon funeral facilities. 2015.
7. The Korea Transport Institute. A study on demand forecasting for airport. Sejong: The Korea Transport Institute; 2012. (Korean).
8. Box GEP, Jenkins GM. Time series analysis, forecasting and control. San Francisco: Holden-Day; 1976.
9. Kim JC, Park JS, Choi YR, Lim JH, Lee JG. Air traffic analysis project: a Study on Forecast of Aviation demand. Korea Transportation Research Institute; 2015.
10. Jung DB. SPSS time-service demand prediction II. Seoul: Hannarae Academy; 2014. (Korean).
11. Jung DB. SPSS time-service demand prediction I. Seoul: Hannarae Academy; 2009. (Korean).
12. Lee PD, Park TH, Kim HW. The supply and demand plans and policy directions of funeral facilities in the city of Suwon. Seongnam: Eulji, Industry-university Cooperation Center; 2017. (Korean).
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||