1. 노출용량 결정

DRMA 첫 적용 단계는 노출 용량을 정하는 것이다. 선정된 논문들 간에는 범주 구간이 서로 다르고 단위도 다를 수 있기 때문에, 메타분석을 수행하는 연구자가 일관된 기준에 따라 용량을 부여해야만 한다. 통상적부여하는 기준은 다음과 같다[2,16].

첫째, 범주를 앞과 뒤 수치(lower and upper boundary of an category)로 제시했으면 해당 범주의 중위수(median)을 용량으로 삼는다. 둘째, 가장 작은 용량의 참조범주(reference)에서 앞이 열려 있으면 앞을 0으로 간주하고 해당 범주의 중위수를 용량을 삼는다. 셋째, 가장 큰 용량 범주에서 뒤가 열려 있으면 바로 앞 범주에서 중위수와 앞 수치 간의 차이값을 마지막 범주의 앞 용량에 더하여 그 범주의 용량으로 삼는다.

이상의 기준을 실제 적용한 것이 Table 1의 dose이다. 이중, Hirota et al. [12]의 용량별 범주는 비흡연자를 참조범주로 하여 10갑년 미만, 10-20갑년, 그리고 20갑년 초과로 제시하였다. 앞서 기준에 따라 용량 범주를 각각 5, 15, 25로 부여하였다. 20갑년 초과 범주의 용량은 10-20갑년의 중위수가 15이므로, 앞 수치 10갑년과 중위수 15갑년의 차이값인 5갑년을 해당 범주 앞 용량인 20갑년에 더한 것이다. 다른 3편도 이와 같은 기준으로 용량을 결정하였다.

2. 용량별 효과 크기 산출

범주형 변수들의 위험도와 95% 신뢰구간(confidence interval, CI)을 활용하여 경향을 추정(trend estimation)하는 DRMA의 표준법은 가중선형회귀모형(weighted linear regressionmodel)을 적용한다. 이때 독립변수는 노출량 수준(expose dose level)이며, 종속변수는 효과 크기로서 로그변환된 위험도(logRR)이다. 가중치는 표본수와 관련이 있는 logRR의 역변량(inverse variance of the logRR)을 사용한다[17].

Table 1처럼 연구 대상 문헌들에서 위험도(RR/OR/HR, 이하 RR)과 95% CI를 제시하고 있다면 이를 활용하여 logRR과 표준오차(standard error, SE)를 계산한다. 위험도를 로그 변환을 시키는 이유는 분포에 대한 가정, 정규성이나 대칭성 가정을 위한 것이다[18]. logRR의 표준오차는 위험도의 95% CI를 알고 있다면, 상한값과 하한값의 로그값의 차이를 3.92로 나누어 산출한다.

3. 적용할 DRMA 분석 모델 선정

앞의 두 준비 과정을 통해 용량을 부여하고 각 용량 범주별 효과크기를 산출하였다면, 그 다음 과정은 선형성(linear trend) 여부에 따라 적용할 모형을 선정하는 것이다.

DRMA 개발에 있어 여러 가지 통계 모형들이 개발되었다. 1992년 Greenland and Longnecker [1]는 참조범주와 각 노출량 범주별(exposure dose level) 위험도의 상관성(correlation)을 일반화 최소제곱모형(generalized least-squares regression)을 활용하여 선형성을 추정하는 방법을 제시하였다. 1993년 Berlin [19]은 용량-반응 관계를 알아볼 다중연구 분석을 위해 변량효과 회귀모형(random effect regression)을 적용한 Two-stage method를 제시하였다. 부연하자면, 개별연구 각각의 회귀계수를 구한다음 개별회귀계수들의 가중평균을 산출해서 전체 계수를 추정하는 두 단계를 거치는 것이다. 하지만 이 방법들은 선형성을 가정하였을 때는 적용가능 하지만 비선형(non-linear) 관계에서는 적합하지 않았다.

그런데, DRMA는 통상 노출량과 반응관계를 구간별로 제시하는데 이는 용량-반응관계의 선형성 가정을 충족하지 못하는 것을 염두에 둔 것이다[20]. 이에 따라, Liu et al. [21]은 비선형성 관계에서 잘 수렴하도록 quadratic random effect모형을 적용하는 방법을 제시하였다. 이를 Orsini et al. [17]가 유동적 비선형 모형(flexible nonlinear)에 따른 restricted cubic spline법을 적용하여 구간별 비선형성을 통계적으로 검정하고 이를 그래프로 명확히 보여주었으며, 이것이 현재의 표준화된 DRMA 모형이다. 따라서 모델 선정은 선형성을 가정하느냐, 비선형성을 가정하느냐에 따라 분석 과정이 결정된다. 다음은 이들을 수행하는 일련의 과정을 설명토록 하겠다.

1. 선형성을 가정한 모형 선정시

여러 개 논문에 있어 선형성을 가정한 DRMA 수행은 Two-stage method를 실시한다[19]. 이는 (1) 개별연구 각각의 선형 회귀계수를 구한 다음, 이들의 가중평균을 산출해서 전체 회귀계수를 추정한다. (2) 그리고 모형적합도(goodness of fit)를 고려하여 이질성 정도를 파악한다. (3) 다음으로 선형성 확인을 위한 추가적인 검정이 필요하다. 이를 위해 restricted cubic spline으로 구간을 세분화하여 각 구간별 선형성 검정을 수행하고, 시각적 이해를 위해 그래프를 작성한다.

이상의 DRMA 분석을 위해 STATA에서는 glst (generalized least squares for trend estimation)를 포함한 다양한 명령어를 제공하고 있다[2]. Table 2는 메타분석을 위한 STATA 명령어를 표로 정리한 것이다.

Table 2.

Related commands on the STATA for dose-response meta-analysis

선형성을 가정한 Two-stage method를 적용하기 위한 STATA 명령어는 < glst logrr dose, se(se) cov(n case) pfirst(id study) ts(f) >이다. 명령문에서 glst 다음에 logRR과 용량변수를 순서대로 넣어야 한다. 쉼표 뒤로는 옵션들이 위치하는데 se(se)는 표준오차이며, cov(n case)는 공변량으로 괄호 안에 전체 표본수(n)와 사건발생수(case)를 입력한다. pfirst(pool-first method) 명령어는 first stage로 개별 연구별로 회귀계수를 산정하라는 옵션이다. 이때 주의할 점은 id는 개별연구를 식별하는 고유 번호를 나타내는 것으로, Table 1의 ‘id’처럼 반드시 숫자로 입력한다(eg. Hirota 1993, ‘1’; Shibata 1996, ‘2’). 그리고 study는 연구설계(study design) 종류를 나타내는 것으로 환자-대조군 연구는 ‘1’, 발생밀도(incidence-density) 코호트 연구는 ‘2’, 그리고 누적발생(cumulative incidence) 코호트 연구는 ‘3’ 숫자를 입력하도록 사전에 정해 놓았다. Table 1의 4편 모두 환자-대조군 연구라서 ‘1’로 기록되었다. ts는 two stage를 나타내며, ts(f)는 second stage에서 fixed effects 모형을 사용하라는 의미이다. 만약 이질성을 고려한다면 ts(r), 즉 random effects 모형을 옵션으로 사용한다.

Figure 1은 Table 1의 자료에 상기 명령어를 수행하여 얻은 결과이다. DRMA에서 이질성은 개별 연구들 간의 기울기(회귀계수)의 차이가 없다는 것을 귀무가설로 설정하며, 만약 이를 기각한다면(p < 0.05) 연구들 간의 이질성이 있다고 해석한다. 여기서는 이질성 여부를 나타내는 goodness of fit의 p-value가 0.1161로서 이질성이 없다고 해석할 수 있다. 따라서 fixed effect model을 선택하여 선형성을 가정한 전체 회귀계수는 0.0198이다(p = 0.005). 앞선 명령문의 마지막에 eform 옵션을 추가하면 지수화 변환을 한 결과 1.02 (= EXP(0.0198))를 얻어낼 수 있다. 이는 1갑년 증가에 따라 위험도가 2.0% 증가한다는 뜻이다. 만약 10갑년에 해당하는 위험도를 알고 싶다면, 앞서 얻어낸 회귀계수에 용량 10을 곱하여 옵션에 지수변환(eform)을 실시한 값이 1.22 (= exp(10^*0.0193))이다. 이에 따라 10갑년 증가할 때 위험도는 1.22배 증가한다고 해석한다. 10갑년의 용량에 대한 위험도와 이의 95% CI를 구하는 명령어는 < incom dose*10, eform >이다. Lincom (linear combinations of estimators)은 STATA에서 회귀계수를 지수변환하는 명령어이다.

Figure 1.

Results of dose-response meta-analysis for multiple studies in Table 1.

선형성을 가정하고 분석하였지만, 비선형성을 가정할 경우 얼마나 차이가 있느냐를 살펴볼 필요가 있겠다. 추후 비선형성을 가정한 위험도와 비교를 하기 위해서는 Two-stage method로 산출된 회귀계수를 각 용량변수별로 곱하여 logRR을 계산한다. 명령어는 < predictnl lrr_lin = _b[dose]^*dose >이며 아래에서 해당 수식으로 나타내었다.

ln (RR_ij) for non-referent RR, X₀ is reference category (RR=1, lnRR=0). β = regression coefficient from glst (generalized least squares for trend estimation). i = study; j = dose level.

선형성을 가정한 용량별 위험도를 구하였다면 이를 지수변환하여 새 변수로 만드는 명령어는 < gen rr_lin = exp(lrr_lin) >이다. 상기 명령어를 실행하면 데이터 열람창에서 lrr_lin과 rr_lin의 새 변수가 추가된 것을 확인할 수 있다.

2. 비선형성을 가정한 모형 선정시

용량-반응에 대한 위험도가 선형적인 관계를 보이지 않는다고 판단되면 선형성 검정을 실시하는데, 이를 위해서는 용량 범주를 세분화하여 범주별 용량-반응에 대한 위험도를 확인해 보아야 한다. 이때 고려해야 할 것은 개별 연구들의 용량이 동일하지 않다는 점과, 만약 용량-반응에 대한 위험도가 비선형적 관계라면 용량범주의 구간 설정에 문제가 생길 수 있다는 점이다. 따라서 비선형성 관계에서 용량범주 설정에 있어 최적의 접근은 restricted cubic spline을 사용하여 구간을 세분화하는 것이다[22,23].

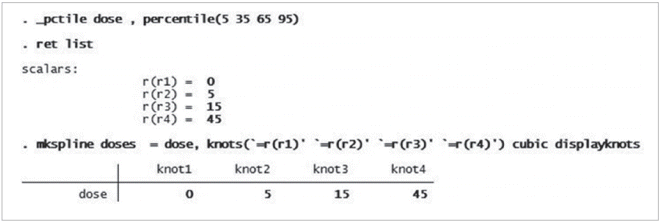
비선형성을 가정한 분석의 첫 번째 수행 과정으로 용량범주를 세분화한 다음, 해당 구간별 실제 용량을 배정하기 위하여 < _pctile dose, percentile(5 35 65 95) > 명령어를 실행한다. 이는 용량을 5, 35, 65, 95 percentile을 구간화시킬 지점(knot)으로 세분하여 프로그램 메모리에 임시 저장시키라는 뜻이다(Figure 2). 만약 메모리에 저장된 구간별 실제 용량값을 확인하려면 < ret list > 명령어를 실행하면 되고, 앞서 4개 구간별 knot r(r1), r(r2), r(r3), r(r4)에 해당하는 실제 용량을 0, 5, 15, 45임을 확인할 수 있다(Figure 2). 이렇게 용량을 세분화한 다음, STATA가 제공하는 restricted cubic spline 을 수행하기 위하여 < mkspline doses = dose, knots(’=r(r1)’ ‘=r(r2)’ ‘= r(r3)’ ‘= r(r4)’) cubic displayknots > 란 명령어를 실행한다. Mkspline (linear and restricted cubic spline construction)과 cubic 옵션에 따라, 설정한 용량 구간별로 restricted cubic spline 실시하여서 knots (용량구간 설정값, 여기서는 4) 수에서 하나 작은 수의 구간인 (doses1, doses2, doses3) 만들어 진다.

Figure 2.

An example of the restricted cubic spline.

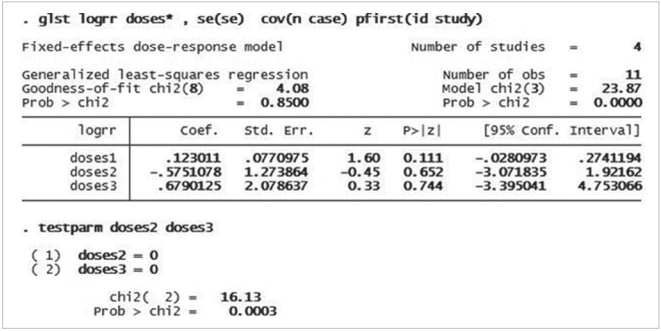
두 번째 수행 과정으로 각 연구별로 정해놓은 용량 구간별 회귀계수를 산출하고, 비선형성 여부를 확인한다. 이를 위한 명령어는 < glst logrr doses^*, se(se) cov(n case) pfirst(id study) >이다. 상기 명령어는 restricted cubic spline으로 생성되는 각 용량 구간별 회귀계수를 산출한 것이다. 선형을 가정한 DRMA와 다른 것은 ts(f) 옵션이 빠져있다는 점이다. 그 결과 회귀계수가 doses1은 0.123, doses2는 -0.575, 그리고 doses3은 0.679임을 알 수 있다(Figure 3). 산출한 세 구간별 회귀계수가 선형성을 갖는가를 알아보기 위하여 < testparm doses2 doses3> 명령어를 수행한다. Testparm은 STATA에서 선형성 여부를 Wald test로 검정하는 명령어이다. Restricted cubic spline의 특성상 doses1 구간은 original dose의 값이므로 제외하며, 선형성 관계를 검정하기 위하여 doses2와 doses3의 joint 기울기가 선형성이라는 귀무가설을 검정하는 것이다(H₀: β₁=β₂ = 0). p-value가 0.05보다 크면 귀무가설을 받아들여 선형성이 있다고 판단하며, 0.05 이하이면 비선형성으로 해석한다[22]. Figure 4의 testparm chi-squarep-value가 0.0003으로 귀무가설을 기각하여 본 연구는 흡연량이 증가에 따른 대퇴골두 무혈성괴사 위험도는 비선형 관계가 있음을 알 수 있다.

Figure 3.

Results of the linearity test for multiple studies in Table 1.

Figure 4.

Dose-response relations between linearity and non-linearity model.

세 번째 수행 과정으로 비선형을 가정한 logRR과 95% CI를 산출하기 위하여 < predictnl logrrwithref = _b[doses1]^*doses1+_b[doses2]^*doses2+_b[doses3]^*doses3, ci(lo hi)>란 명령어를 입력한다. 상기 명령어는 첫 번째 수행 과정에서 restricted cubic spline으로 부여한 구간별 용량과 두 번째 수행 과정에서 산출한 구간별 회귀계수를 곱하여 합산한 다음, 비선형성을 가정한 logRR과 95% CI를 추정하라는 의미이며 아래에서 수식으로 나타내었다.

ln (RR_ij) for non-referent RR, X₀ is reference category (RR=1, lnRR= 0). β =regression coefficient from glst(generalized least squares for trend estimation). i = study; j = dose level.If knots is 4, regression coefficient (β₁, β₂, β₃) and dose group (X₁, X₂, X₃) be created using restricted cubic spline

비선형성을 가정한 용량별 위험도를 구하였다면 이를 지수변환하여 새로운 변수로 만드는 명령어는 < gen rrwithref= exp(logrrwithref)> 이다. 만약 95% CI의 하한값과 상한값에 대한 지수변환을 하려면 < gen lbwithref = exp(lo) > < gen ubwithref = exp(hi) >란 명령어를 각각 실행한다.

3. 두 모형 간의 비교를 위한 그래프 작성

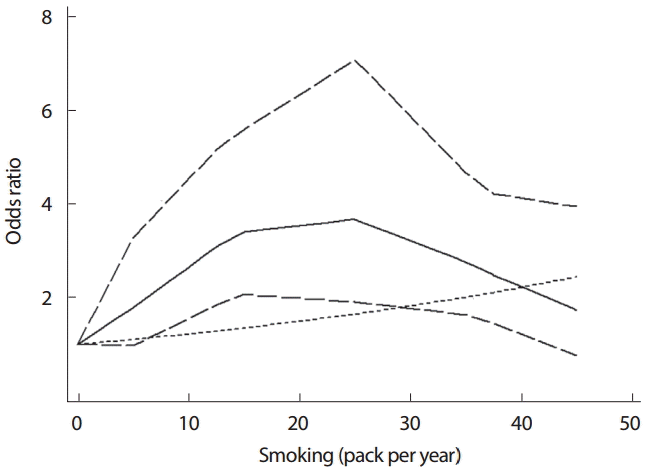
선형성을 가정하여 도출한 결과(Figure 1)와 비선형성을 가정하여 도출한 결과(Table 3)를 상호 비교하기 위하여 하나의 그래프로 제시하기를 권한다. STATA에서는 two-way 명령어를 사용하여 비선형관계를 도식화 할 수 있다. Figure 4를 작성한 명령어는 < twoway (line lbwithref ubwithref rrwithref dose, sort lp(longdash longdash l) lc(black black black)) (line rr_lin dose, sort lp(shortdash) lc(black))>이다.

Table 3.

Overall statistics for dose-response meta-analysis

앞의 괄호는 비선형성을 가정한 위험도 그래프를 작성하라는 의미이며, 뒤의 괄호는 선형성을 가정한 위험도 그래프를 나타내라는 것이다. Figure 1을 설명하면서 산출한 rr_lin 변수를 활용함을 확인하기 바란다. Figure 4에 가는 점선의 선형성 가정 분석과 실선의 비선형성 가정분석을 나타내었다(굵은 점선은 비선형성의 95% CI). 25갑년을 전후로 위험도가 증가에서 감소하는 경향을 보인다는 점에서 비선형으로 해석하는 것이 타당하겠다. 이는 선형성 검정에서의 p-value 값이 0.0003으로 비선형성임을 지지한다(Figure 3, Table 3).

4. 요약효과크기 산출과 숲그림

일반적으로 메타분석은 효과크기를 숲그림으로 제시하는데 단일 연구 내에서 용량별 위험도가 여러 개 있다면 단일 연구 내에서 특정 용량으로 설정한 위험도를 계산한 후 이들을 종합하여 메타분석 한다면 특정용량에 대한 위험도의 효과크기를 계산할 수 있다.

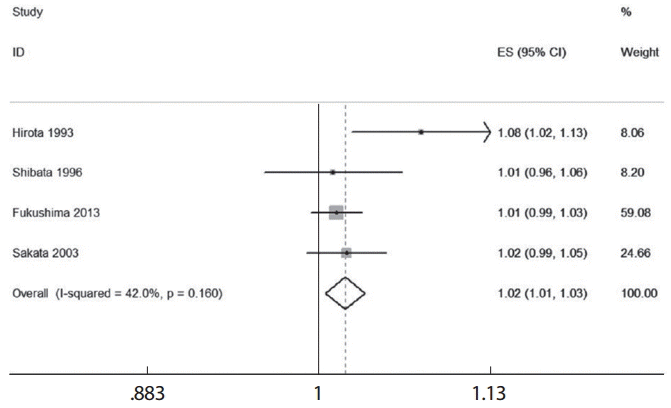
Table 1의 4편의 논문 각각에 있어 요약 효과크기를 산출하기 위해서는 우선 용량의 단위(여기서는 1갑년)를 동일하게 설정한 다음, < glst logrr dose, se(se) cov(n case) cceform > 명령어로 각 논문별로 위험도와 표준오차를 각각 구하고, 그 결과를 이용하여 메타분석을 실시하여 숲그림을 작성한다. 이때 논문 각각의 위험도를 구하기 위해서는 STATA 데이터 열람창에서 해당 연구만을 남겨둔 상태에서 실행하여야 한다. 상기 명령어로 개별 연구의 1갑년에 해당하는 위험도는 1.08 (Hirota 1993), 1.01 (Shibata 1996), 1.01 (Fukushima 2013), 1.02 (Sakata 2003)이었다. 옵션에서 연구설계를 지정하는 것으로 cc는 환자-대조군을, ir은 발생밀도 코호트 연구를 의미한다.

Figure 5에서 4편의 논문 각각에서 1갑년에 해당하는 위험도를 종합한 요약효과크기는 1.02 (95%CI, 1.01-1.03)이었고 I²는 42%를 나타내었다. 요약효과크기는 선형성을 가정한 여러 연구들의 two-stage DRMA 분석에서 1갑년에 해당하는 위험도와 동일하다.

Figure 5.

A forest plot of 1 pack-year on multiple studies. Sources from Table 1.