보건정보 자료를 이용한 나무구조회귀모형의 시각화에 대한 고찰
Visualization with Various Tree-based Regression Results in Health Information Data
Article information
Trans Abstract
Objectives
Among machine learning techniques, a tree-based regression model is widely used as easy to interpret and easy to use results.
Methods
In this study, we examine the characteristics of regression models using various tree structures implemented in R, and apply them to public health data for visual representation and analysis to enhance understanding of the models and data.
Results
We also look at the random forest, gradient boosting model, and xgboost that incorporate the results of various tree-structured model estimates using bagging and boosting, and visualize these estimation processes to compare the results of the model estimates. It also compares the performance of various tree-structured models using various public health data. It visually examines that the performance of the tree-structured models may vary depending on the characteristics of the data.
Conclusions
Through this study, we apply the tree-structured models to public health data to enhance understanding of the data and to help identify and visualize the mechanism of the data.
서 론
나무구조 방법론은 비모수적 기법으로, 데이터의 예측뿐 아니라 설명이 용이한 탐색적 모형(exploratory model)을 만드는 것을 목표로 하는 기계학습 방법 중 하나이다. 회귀나무모형은 비모수적 회귀분석 방법의 하나로, 특정 분포를 가정하지 않고 이진 나무 형태를 이용하여 반응변수와 설명변수 간의 함수관계를 반복적으로 찾아가는 방식이다. 나무구조를 이용하여 모델링을 할 경우, 해석이 용이하고, 데이터의 형태에 따른 가정 혹은 예측변수의 변환이 필요하지 않는다는 장점이 있다. 또한 결측값과 이상치, 다중공선성에 대해 강건한(robust) 방법론이라고 알려져 있다[1].
나무구조 방법론은 의학 분야와 역학 분야에서 특히 유용하게 쓰이고 있다. 나무구조형태의 모형은 질병의 위험인자를 알아내고, 환자들 중 고위험군과 저위험군의 하위 그룹을 식별하는 등 다양하게 활용될 수 있으므로 다중선형모형보다 임상적 결정 규칙을 만드는 데 유용하게 사용될 수 있다. Fonarow et al. [2]은 급성 심부전으로 입원한 환자들의 위험도를 예측하기 위해 나무구조모형을 사용하고 임상적 결정 규칙을 제시하였다. Cheng et al. [3]은 방사선 요법으로 치료를 받은 두경부암 환자들의 체중 감량 정도를 예측하기 위해 나무구조모형을 구축하였고, Karafin et al. [4]은 혈액학적 질환이 있는 환자들에게 적혈구 수혈 시 헤모글로빈 증가분에 영향을 미치는 요인들을 발견하여 수혈 계획 수립 시 고려해야 할 인자들을 제안하였다. 이외에도 Loh et al. [5,6]은 하위 그룹 식별을 위해 두 개 이상의 치료군 데이터에 적용 가능한 회귀나무를 개발하였다. 또한 치료 효과에 대한 신뢰구간을 추정하기 위해 부트스트랩 보정 기술(Bootstrap calibration technique)을 사용하였고, 하위 그룹 식별을 위해 나무의 각 노드에 주성분(principal components) 혹은 판별식(linear discriminants) 변환을 적용하여 지역 의존성(local dependencies)을 고려하는 나무를 개발하기도 하였다. Dusseldorp and Meulman [7,8]은 치료군과 순서형 종속 변수들 간의 상호작용을 고려하기 위해 먼저 선형 주효과 모형을 적합시키고, 잔차를 이용하여 각 치료군에 조각상수 회귀나무를 적용하여 회귀나무와 선형회귀를 결합한 회귀 간선 접근법(Regression Trunk Approach, RTA)을 제안하였다. 2010년에는 RTA를 선형회귀와 나무모형을 동시에 추정할 수 있도록 개선한 Simultaneous Threshold Interaction Model (STIMA)를 개발하였다.
나무구조모형의 가장 큰 장점은 모형 추정의 결과에 대한 해석이 용이하고 결과를 다양한 방법으로 시각화하여 자료에 대한 직관을 높일 수 있다는 것이다. 또한 고차원 데이터의 경우에는 이러한 장점이 더욱 부각될 수 있다. 나무구조모형은 기본적으로 자료의 공간을 분할하고 분할된 공간에서 추정을 하는 방법이므로 다차원 공간상의 자료를 각 분할 공간상에서 시각적으로 설명함으로써 자료에 대한 이해를 높일 수 있고 이를 통하여 임상 연구 분야에서 자료의 매커니즘을 파악하는데 큰 도움을 줄 수 있다.
본 연구에서는 다양한 형태로 개발되어 있는 회귀나무들 중 R에서 사용할 수 있도록 개발되어 있는 다양한 회귀나무모형들을 중심으로 모형추정 알고리즘들의 특징과 차이점을 살펴보고 이를 보건자료에 적용했을 때 시너지 효과를 낼 수 있는 장점들을 살펴본다. 또한 각각의 회귀나무모형 추정결과를 시각화하는 방법을 정리하고 실제 보건자료를 이용하여 시각화하여 추정결과를 좀 더 유용한 형태의 정보로 제공, 보건자료에 대한 이해를 높일 수 있는 방안에 대한 새로운 방법을 제시하고자 한다.
연구 방법
나무구조를 이용한 다양한 회귀방법들
Automatic Interaction Detection (AID) [9]는 처음으로 개발된 회귀나무로 불순도의 합을 최소화하는 방향으로 이진 분할을 반복적으로 진행하다가 미리 지정된 수준보다 불순도의 감소량이 더 적으면 분할을 멈추어 최종나무모형을 결정한다. 최종 노드의 값으로는 각 노드에 할당된 자료값들의 표본 평균을 사용하며, 이를 예측된 Y값으로 삼는다. AID는 데이터를 과적합하는 경향이 있고, 두 개 이상의 변수들이 서로 높은 연관관계가 있는 경우 변수 선택에 편향이 있을 수 있다는 문제가 제기되었다[10,11]. 1984년에 이르러 제안된 Classification and Regression Tree (CART) [12]는 AID방법을 개선한 방법으로 지금까지도 가장 널리 쓰이는 나무 방법론 중 하나이다. CART는 AID와 같이 탐욕적 탐색(greedy search) 접근방식을 사용하지만, 가지치기 방법을 이용하여 과적합 문제를 해결하고 있다. AID와 CART는 노드의 불순도 함수로 편차의 제곱합을 사용하였고, 예측값으로는 각 노드에 할당된 관측들의 평균값을 사용하고 있다. 즉, 회귀나무는 설명변수의 공간을 분할하고 분할된 공간 각각에서 상숫값을 갖는 조각 상수(piecewise constant) 회귀의 형태가 된다. 이후 회귀나무는 상수가 아닌 선형 혹은 더 높은 차수의 모델을 구축하거나 분할 변수의 선택을 효율적으로 하는 방향으로 발전하였다. M5 [13]와 M5P [14]는 조각 다항선형 나무를 만들고 최종 노드에서 평균값 대신 다중선형회귀함수를 이용하여 더 빠르고 정확한 방법론을 사용하였다. Torgo [15]는 회귀나무모형의 예측을 높이기 위해 최종 노드에 선형모델 이외에도 커널을 이용한 회귀와 최근접 이웃 모델 등을 다양하게 적용하였다.
최종 노드에 높은 차수의 모형을 구축하는 것 외에도 새로운 접근방식으로 통계적 검정을 이용하는 방법들도 개발되었다. Smoothed and Unbiased Piecewise Polynomial Regression Trees (SUPPORT [16])는 각 노드에서 먼저 데이터에 대하여 회귀모형을 적합하고 잔차를 구한 후, 관측치들을 그들의 잔차의 부호에 따라 두 집단으로 분류한다. 그 후에 모든 설명 변수들에 대하여 두 집단 간 차이에 대한 t-검정을 수행하고 이들 중 제일 유의미한 변수를 해당 노드를 분할하는데 사용한다. 이때의 분할점은 두 집단 각각에서 구한 해당 설명변수의 평균값들의 평균값이 된다. 그 결과, 각 노드에서는 단 하나의 선형 모델만 적합시키면 된다. SUPPORT에서는 변수 선택에 편향이 발생할 수 있다. 이를 보완하기 위해서 Generalized, Unbiased, Interaction Detection and Estimation (GUIDE) [17]에서는 노드 분할과 최종 노드에서의 적합을 위한 변수의 유의성을 결정하는 유의확률을 낮추는 방법으로 부트스트랩 캘리브레이션(bootstrap calibration)을 적용하였다. Conditional Inference Tree (CTREE)[18]는 변수선택에 편향이 없는 알고리즘으로 조건부 추론 절차를 이용하여 재귀분할을 수행하는 회귀나무이다. 편향되지 않는 변수 선택을 가능하게 한다. 이 외에도 Kim et al. [19]과 Loh [20]는 나무 형성 시에 각 노드에서 하나 혹은 두 개의 회귀인자를 사용하여 데이터 시각화에 용이하도록 하였다.
R에서 제공되고 있는 다양한 회귀나무 추정방법들
다양한 형태의 회귀나무들이 통계 프로그래밍 플랫폼인 R에서 사용할 수 있도록 개발되어있다. 개발되어 있는 회귀나무들은 크게 두 가지 형태로 나눌 수 있다. 첫 번째는 하나의 나무구조로 추정을 하는 방법으로 기존에 개발된 대부분의 방법이 이에 해당된다. 두 번째는 나무구조의 불안정성을 보완하기 위하여 배깅(bagging)과 부스팅(boosting) 방법을 이용한 앙상블(ensemble) 기법을 이용하는 것이다.
R에서 제공하고 있는 회귀나무들의 성능을 비교해 보기 위해 71명의 건강한 독일 여성으로부터 측정한 bodyfat 자료를 이용하였다[21]. 이는 체지방(DEXfat) 예측을 위하여 측정한 신체 각 부분의 피부 두께(anthro3a, anthro3b, antro3c, anthro4), 뼈의 넓이(elbowbreath, knee-breath), 둘레(waistcirc, hipcirc) 등에 대한 자료로 R의 TH.data 패키지에서 제공하고 있다. 회귀계수들의 크기 비교를 위하여 모든 변수들은 표준화하여 사용하였다.
단일트리방법
단일트리방법은 추정의 안정성은 떨어지지만 해석이 직관적으로 매우 용이하다는 점에서 자주 이용되고 있다.
Rpart와 tree
CART [12]는 나무구조의 각 마디에서 하나의 설명변수를 선택하고 이를 이용하여 두 개의 자식 노드로 분리하는 이진나무로 회귀나무는 오차에 대한 제곱합을 감소시키는 방향으로 노드를 분리하여 나무를 성장시킨다. 그 후 과적합을 막기 위해 교차검증을 이용한 가지치기 과정을 거치게 된다. 가지치기까지 완료되면, 마지막 노드에 할당된 자료들의 종속변수의 평균을 계산하여 이를 추정값으로 이용한다. CART는 데이터 마이닝(data mining)에서 가장 잘 알려진 회귀나무 기법 중의 하나이지만, 변수 선택 시 편향이 있을 수 있다고 알려져 있다.
Rpart와 tree 패키지는 모두 CART [12]의 이진나무모형을 구현해 놓은 R 패키지로 tree는 기존에 S 언어로 구현되어 있던 tree 함수를 R로 구현해 놓은 것이며 rpart는 결측치까지를 고려한 CART 알고리즘을 R로 구현해 놓은 것이다. 현재 rpart 패키지는 대부분 C언어를 기반으로 하고 있어 tree에 비해 계산속도가 빠른 장점이 있다. 또한 rpart는 가지치기 과정까지가 포함되어 있으나 tree는 가지치기를 따로 해주어야 한다.
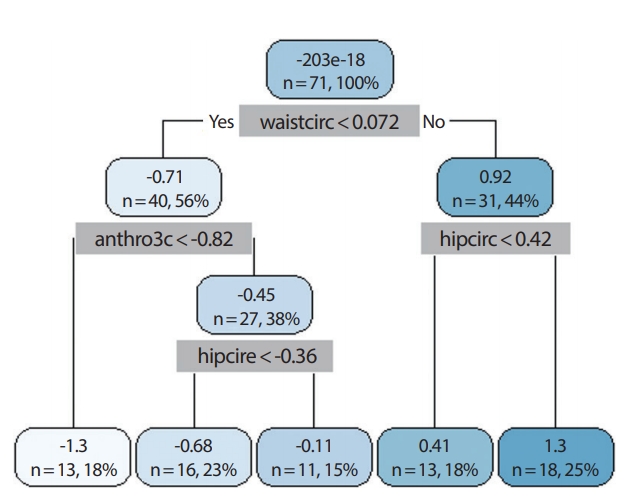
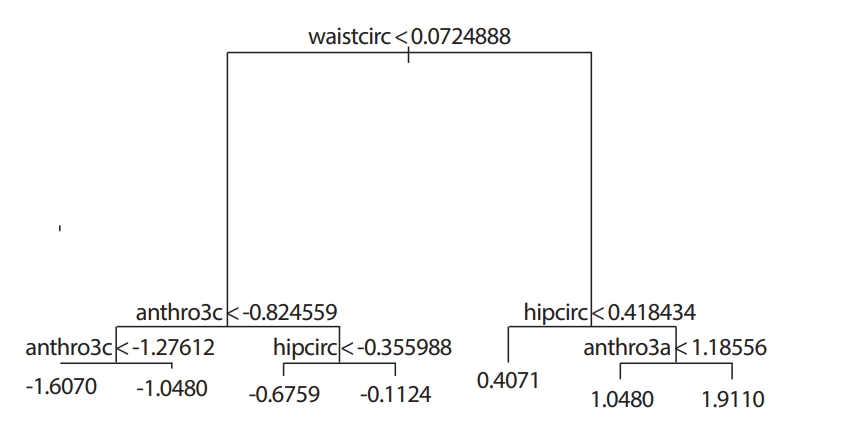
Figure 1은 Bodyfat 자료에서 DEXfat을 추정하기 위해 9개의 모든 변수를 이용한 rpart 결과로 waistcirc, anthro3c, 그리고 hipcirc 변수를 이용하여 DEXfat을 추정하고 있다. tree의 결과에서는 anthro3a 변수까지 이용하고 있다(Figure 2). rpart 결과의 경우 rpart.plot 패키지의 rpart.plot 함수와 rattle패키지의 fancyRpartPlot함수를 사용하여 각 노드에 대해 각 노드에 대한 예측값, 관측수의 백분율 등 좀 더 많은 정보를 보다 심미적으로 표현할 수 있다.
Rweka의 M5P
Weka는 자바로 개발된 기계학습을 위한 소프트웨어로 자료 준비, 분류, 회귀, 군집분석, 연관규칙, 그리고 자료 시각화 등에 관련된 모든 함수들을 포함하고 있다. 뉴질랜드의 Waikato 대학에서 개발하였으며 무료로 이용할 수 있다. 최근 R에서 Weka를 이용할 수 있도록 해주는 R interface인 Rweka가 개발되어 R에서도 편리하게 사용할 수 있다. Weka에서 제공하고 있는 M5 [13]는 CART와 같은 형태인 오차제곱합을 불순도 함수로 사용하고 있지만 최종 노드에서는 종속변수들의 평균값 하나를 사용하는 대신 다중선형회귀함수를 이용하여 예측의 정확도를 개선하였다. M5P [14]에서는 최적의 분할을 찾기 위해 각 노드에서도 다항 선형 나무를 이용하여 속도를 개선하였다.
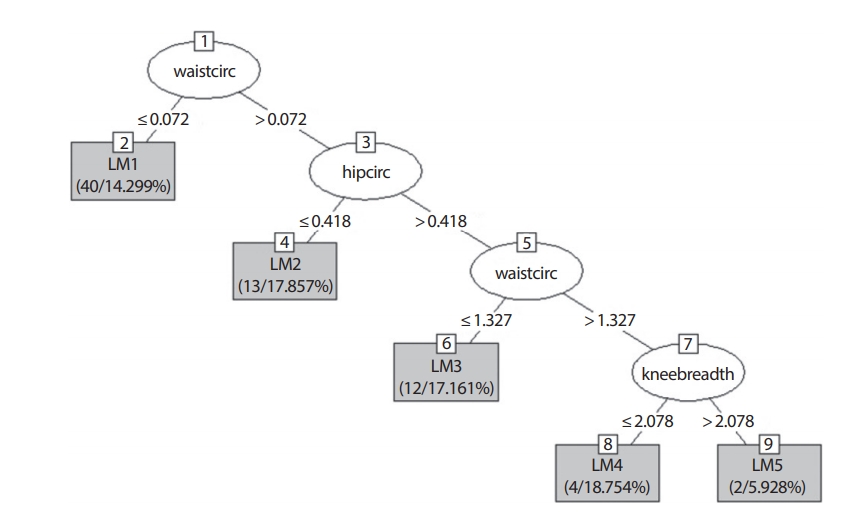
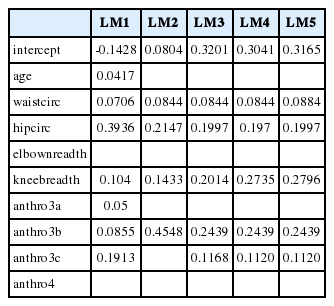
Figure 3의 M5P의 결과에서 처음 두 노드의 분할 규칙은 앞의 rpart와 tree와 같이 waistcirc와 hipcirc를 사용하고 있으며 분할점도 0.072와 0.418로 같다. waistcirc가 작은 노드에서는 hipcirc와 anthro3c의 회귀계수가 크게 나타나고 있어 rpart나 tree의 결과와 같이 중요변수라고 생각할 수 있다. waistcirc와 hipcirc값이 모두 큰 쪽의 노드에서는 kneebreadth가 중요변수로 나타나고 있어 rpart나 tree와는 다른 결과를 보이고 있다. 이는 DEXfat의 큰 값에서는 kneebreadth가 중요 역할을 함을 확인시켜주는 것이다. 또한 각 최종 노드의 추정 식에 대한 계수들을 살펴보면 kneebreadth, anthro3b, 그리고 hipcirc가 중요한 역할을 하고 있음을 알 수 있다(Table 1).
Ctree와 evtree
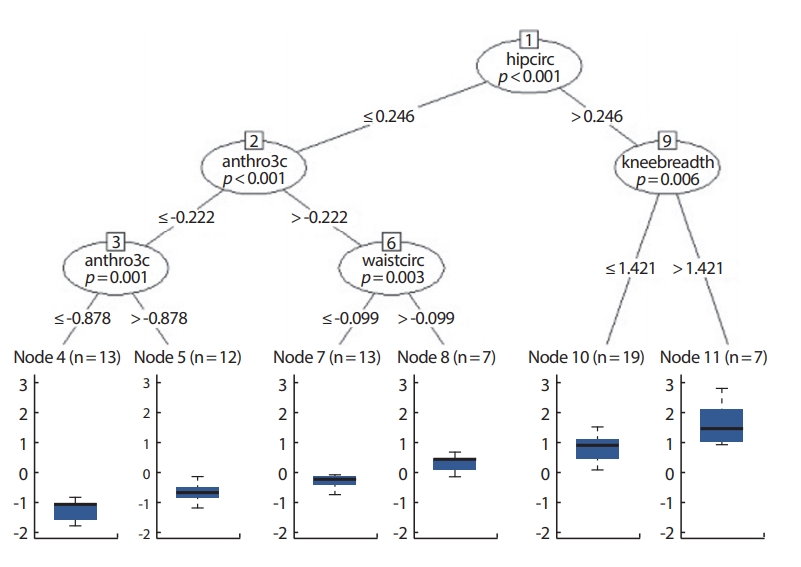
기존의 나무구조모형의 가장 큰 문제점은 각 노드에서의 분리점을 찾기 위해 전체탐색(exhaustive search)을 한다는 것이다. 이로 인하여 계산이 오래 걸릴 뿐 아니라 과적합과 각 노드에서의 변수 선택에 있어서 편의가 발생할 수 있다. 과적합을 방지하기 위해서 가지치기를 사용하기도 하지만 각 노드에서의 변수 선택에 대한 편의성은 여전히 남아있다. 이를 보완하기 위하여 조건부 추론을 이용하여 반복적인 분할을 하는 조건부추론나무(conditional inference tree, CTREE) [18,22]가 개발되었다. Party패키지에 구현되어 있으며, 각 노드에서 분할을 위한 변수를 선택하는 과정과 선택된 변수를 이용하여 분할점을 찾는 과정을 독립적으로 진행한다. 먼저 조건부 분포를 통해 반응변수와 설명 변수간의 독립성을 알아보고, 검정통계량과 유의확률을 이용하여 분할에 사용할 변수를 선택한다. 변수 선택 후 분할점을 찾기 위해서도 조건부 분포를 이용한다. 마지막 노드에서는 조건부 가중평균을 구하여 추정값으로 이용한다. ctree에서는 별도의 가지치기 과정이 없으며, 명목형, 순서형, 숫자형, 절단형 그리고 다변량까지 모든 종류의 반응변수에 대해 회귀분석 적용이 가능하다.
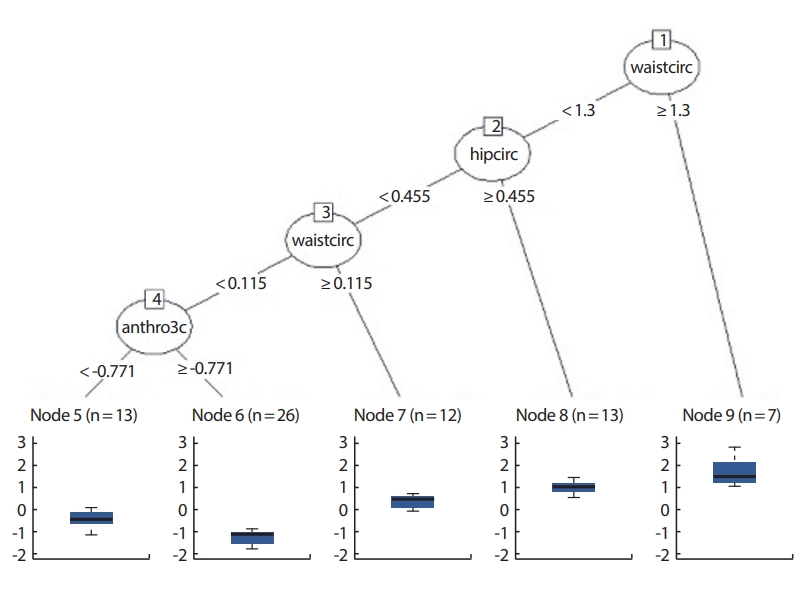
대부분의 나무모형에서는 자료 공간을 분할하고 각 분할된 공간에서 같은 방식으로 분할을 해 나가는 형태를 반복적으로 이용하여 모형을 적합시켜 나간다. 이는 효율적인 것처럼 여겨지고 있으나 각 분할 공간 내에서만 최적화를 시키게 되므로 국지적으로 최적화가 될 경향이 크다. 이러한 단점을 극복하기 위하여 진화알고리즘을 이용, 나무모형 전체를 고려하여 최적화하는 방법이 제안되었다. 이는 evtree 패키지에 구현되어 있다.
Ctree는 다른 나무구조와는 달리 첫 노드에서 hipcirc를 이용한다(Figure 4). 그리고 hipcirc가 큰 쪽에서는 kneebreath를 이용하여 DEXfat이 큰 값일 때에는 kneebreadth가 중요 역할을 한다는 M5P와 같은 결론을 나타낸다. hipcirc가 작은 쪽에서는 antrho3c와 waistcirc를 이용하여 이 또한 rpart, tree, 그리고 M5P와 같은 결론이다. evtree는 다른 나무구조와 비슷하게 waistcirc, hipcirc, 그리고 anthro3c를 이용하여 나무를 구성하고 있다(Figure 5).
배깅과 부스팅을 이용하여 다량의 나무모형을 이용한 방법
나무구조의 가장 큰 단점은 추정모형이 불안정하다는 것이다. 즉, 자료가 달라지면 추정모형이 크게 달라질 수 있다는 것이다. 이를 보완하기 위하여 배깅방법[23]과 부스팅방법[24]을 이용하여 나무모형을 여러개 추정한 후 결과를 취합하여 이용하는 앙상블 기법들이 개발되었다.
randomForest
랜덤 포레스트[25]는 여러 개의 나무모형을 구성한 후 결과를 취합하는 앙상블 기법 중 하나이다. 각 나무는 무작위로 추출된 관측들로 이루어진 부트스트랩 샘플을 이용하여 만들어지며, 많은 수의 나무(500-2,000개)로 이루어져 ‘랜덤 포레스트’라고 불린다. 각 나무는 가지치기 없이 최대 크기로 성장하고 있으며, 각 노드에서는 미리 지정된 수의 변수들을 무작위로 선택하고, 선택된 변수들만을 이용하여 최상의 분할을 선택하고, 최종 노드의 값으로는 각 나무로부터 얻은 값들의 평균을 이용한다. 각 나무 구성시 뽑히지 않은(out-of-bag, OOB) 샘플을 사용하여 편향되지 않은 오분류율과 변수 중요도를 계산할 수 있으므로 따로 테스트 자료를 이용해야 하거나 교차 검증을 할 필요가 없다. 관측들과 변수들을 무작위로 추출하여 이용하므로 트리 간의 다양성을 유도하면서 예측 강도를 유지할 수 있다. 수많은 나무들을 구성하여 개별 나무를 검사하는 것은 의미가 없으므로 랜덤포레스트는 ‘블랙 박스’ 접근으로 볼 수 있고 선형 회귀 모형에 비해 각 변수의 해석이 어렵지만, 자료의 해석에 도움이 되는 다양한 값들을 제공한다. 이 중 변수 예측도는 해당 예측 변수의 데이터가 무작위로 치환된 경우 예측이 얼마나 악화될지에 따라 평가된다. 결과 테이블을 사용하여 예측 변수 간의 상대적 중요성을 비교할 수 있다.
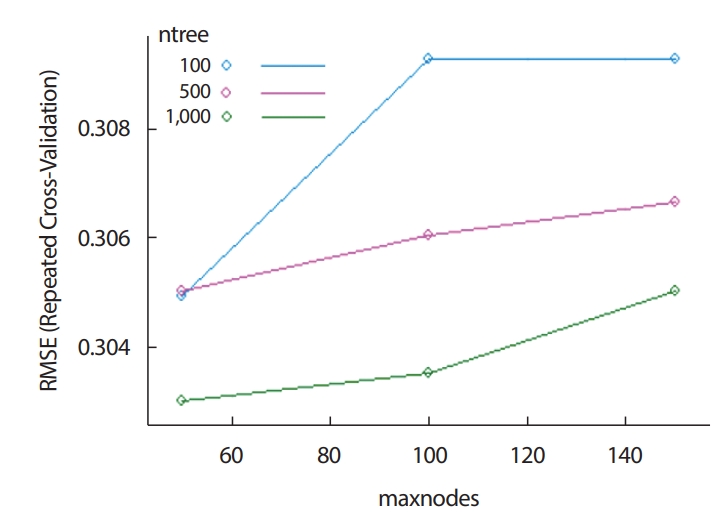
랜덤포레스트는 과적합 문제를 방지하기 위해 교차타당성 검사를 통해 조정된 초모수(hyperparameters)를 찾아 사용할 수 있고, 이 때 적정한 초모수값을 찾기 위해 지정한 범위 안에서 그리드 탐색 기법을 사용한다. 본 분석에서는 관심이 있는 초모수로 ntree와 maxnode두가지를 이용하였다. ntree는 나무의 수, maxnode는 각 나무에서 노드의 최대 개수를 의미한다. 이러한 파라미터 조정을 이용해서 잔차제곱 평균의 제곱근값(RMSE)을 기준으로 가장 적절한 초모수를 골라 오버피팅을 방지할 수 있다. 이를 위하여 100개, 500개, 1,000개의 나무 수와 50개, 100개, 150개의 maxnode의 가능한 모든 조합을 이용하였고, 각 경우의 추정된 RMSE를 그림으로 그린 결과는 Figure 6에 나타나있다. 각 ntree에서 모두 maxnode 수가 커질수록 RMSE값이 커짐을 볼 수 있다. 이를 통하여 maxnode가 증가할수록 오버피팅 문제가 심각해짐을 알 수 있다. 또한 ntree의 개수가 1,000개일 때에 RMSE 값이 가장 작음을 알 수 있다. 이로써 최적의 초모수값은 ntree는 1,000개, maxnodes는 50개로 추정되었다. 이렇게 추정된 랜덤포레스트로 예측 변수들이 모델에 미치는 영향력을 계산하여 각 예측 변수의 중요도를 출력할 수 있다.
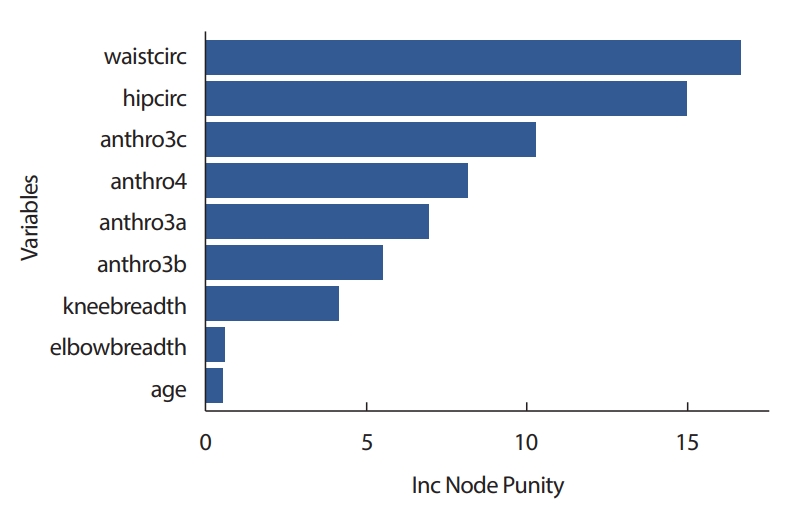
randomForest에서는 중요한 변수들을 판단할 수 있는 값인 변수들에 대한 중요도값과 각 관측에 대한 유사도에 대한 정보를 제공하고 있다. 이를 시각화하여 살펴봄으로써 자료에 대하여 좀 더 많은 정보를 얻을 수 있다. Figure 7은 제공하는 변수들의 중요도를 시각화한 것으로 IncNodePurity값이 클수록 중요도가 커짐을 나타낸다. waistcirc가 가장 중요한 변수로 이용되고 있으며, hipcirc가 두 번째로 중요한 변수가 됨을 나타내고 있다. anthro3c, anthro3a, anthro4는 그 다음으로 중요한 변수이며 서로는 미미한 차이를 보이고 있다. kneebreath 변수의 중요도는 상당히 낮은 편이다. 기본 randomForest 패키지 외에도 랜덤포레스트의 구조와 변수의 역할을 이해를 돕기 위한 randomForestExplainer 패키지가 개발되어 있다. 이 패키지를 통해 다양한 유형의 변수 중요도 측정 및 변수들간의 교호작용에 대해 파악할 수 있다. Min_depth_distribution 함수는 예측 변수들의 평균 최소 깊이의 분포를 조사할 때 사용된다. Depth는 예측 변수들이 각 트리에서 처음 나타나는 지점을 나타내는 것으로 root node 근처에 있을수록 depth는 0에 가까워지며 중요변수로 파악될 수 있다. Figure 8은 1,000개의 tree 중 각 나무에서의 최소 깊이의 분포와 평균값을 나타내고 있다. 회색으로 나타난 NA는 tree에서 쓰이지 않고 있는 경우를 나타낸다. elbowbreath의 경우 200개 가량의 tree에서 쓰이지 않고 있음을 알 수 있다. hipcirc와 waistcirc의 평균 최소 깊이는 각각 1.61, 1.63으로 두 설명 변수 모두 depth 0, 1에서 대부분 나타나고 있으며 DEXfat을 설명하는 데에 중요한 역할을 하고 있음을 알 수 있다. 이는 변수 중요도에서의 결과와 같다.
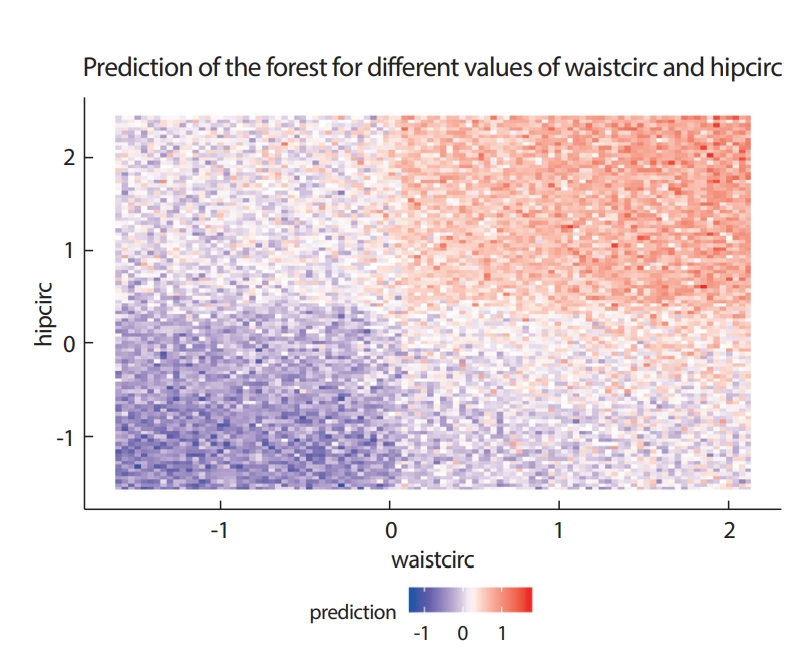
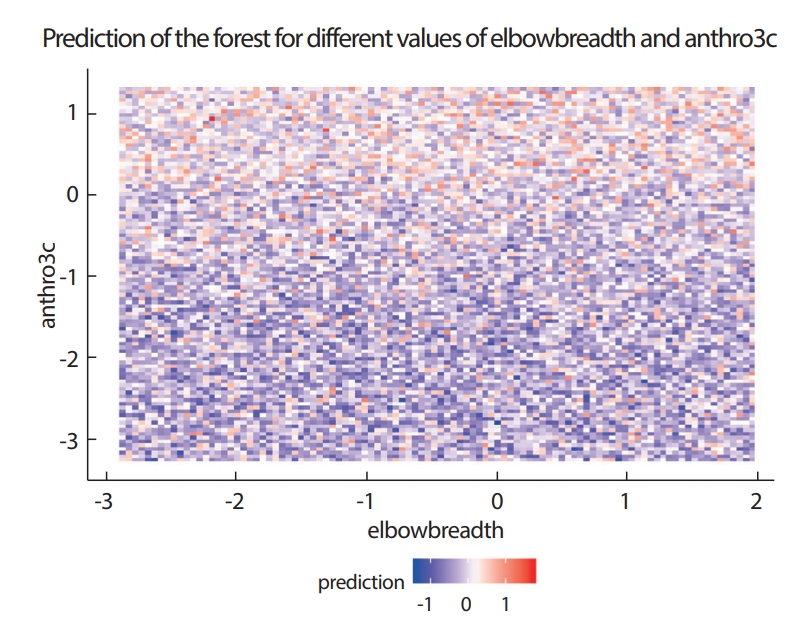
교호작용은 두 변수 사이의 최소 깊이 차이로 나타낼 수 있으며 이들의 평균을 그림으로 나타낸 것을 최소 깊이 상호작용 그림이라 한다 (Figure 9). 최소 깊이의 평균(mean_min_depth)이 작을수록 두 변수가 차례로 나오는 경향이 있으므로 교호작용이 크다고 할 수 있다. Occurrence는 tree에 두 변수가 함께 나오는 횟수를 의미한다. hipcirc과 waistcirc 변수는 최소 깊이 상호작용 그림에서 볼 수 있는 가장 빈번한 상호작용이라고 할 수 있다. Figure 10은 이들의 교호작용을 확인하기 위하여 hipcirc와 waistcirc에 따른 DEXfat의 예측값을 색으로 나타낸 것으로 hipcirc와 waistcirc값이 클수록 DEXfat도 크고, hipcirc와 waistcirc값이 작을수록 DEXfat도 작은 것을 알 수 있다. 반면 상호작용이 가장 적다고 나타난 anthro3c와 elbowbreath의 경우 특정 패턴을 찾아볼 수 없다(Figure 11).
gbm과 xgboost
그래디언트 부스팅(Gradient Boosting Model, GBM) [26,27]이란 Gradient Descent와 Boosting의 합성어로 경사하상을 이용하여 기울기가 낮은 쪽으로 이동시키면서 손실함수를 최소화하는 방향으로 최적화하여 모델함수에 대한 근사치를 찾는 과정을 말한다. 즉, 자료를 잘 설명하지 못하는 모델들을 모아서 손실함수를 최소화하는 최종의 모델함수를 찾는 방법이다. xGBoost [30]는 그래디언트 부스팅을 분산환경에서도 실행할 수 있도록 구현해 놓은 것이다. R에서는 gbm [31]과 xgboost [32] 라이브러리로 제공되고 있다. 이 방법들 또한 변수에 대한 중요도 정보를 제공하고 있다.
gbm에서는 변수 중요로도 상대적 영향력을 계산해 준다. 이는 각 변수가 자식 노드로 분할할 때에 MSE를 감소시키는 정도를 나타낸다. 상대적 영향력의 값이 클수록 감소량이 큰 것을 나타낸다. bodyfat 자료에 대한 변수 중요도(rel.inf)의 상위권은 randomForest의 결과와 비슷하게 waistcirc와 hipcirc, 그리고 anthro3c, anthro3b가 차지하고 있다 (Figure 12). 그러나 randomForest와는 달리 kneebreath가 anthro3a보다 높은 위치를 차지하고 있다. Figure 13은 xgboost에서 각 변수들이 나타나는 빈도를 그림으로 나타낸 것으로 다른 방법들과는 달리 kneebreadth가 중요도 3위를 차지하고 있으며 age도 상당한 우위를 차지하고 있다.
BartMachine
베이지안 가법 회귀모형(Bayesian Additive Regression Model, BART) [31]은 앙상블 기법 중 하나로 여러 개의 나무 모형을 생성하고 이들을 취합하여 최종 모형을 생성하는 방법이다. 다른 방법들과의 차이점은 부스팅 방법에서 이용하고 있는 가중치 대신 사전분포를 이용하고 있으며, 배깅을 이용하여 반복적으로 적합시키는 대신 베이지안 역적합(Bayesian backfitting)을 이용한다는 점이다. bayesTree는 처음 제공된 R 패키지로 일반적인 베이지안 기법의 문제인 계산량이 많아 모형 적합을 위한 계산시간이 문제를 가지고 있다. bartMachine [32]은 Java를 기반으로 한 소프트웨어로 R에서도 사용할 수 있도록 패키지를 제공, BayesTree보다 계산시간을 크게 단축시키고 있으며, 결과를 다양한 방법으로 살펴볼 수 있는 함수들을 제공하고 있다.
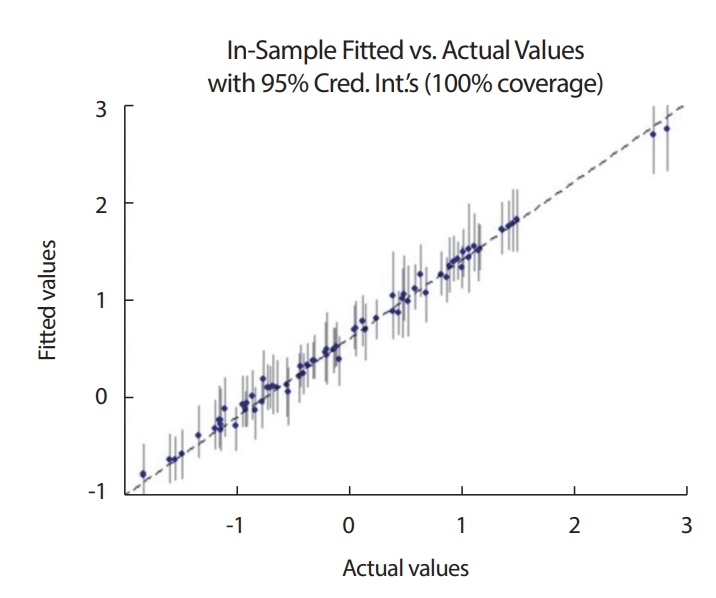
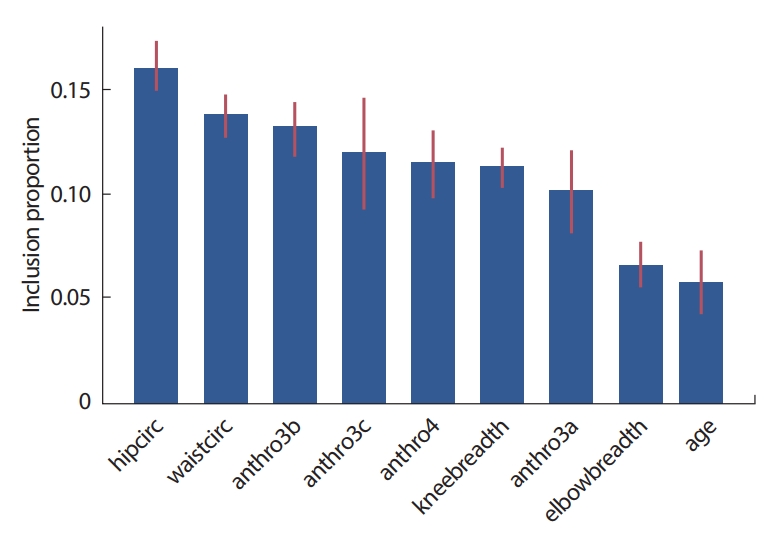
Figure 14는 원자료와 추정값, 그리고 추정값에 대한 95% 신뢰구간에 대한 그림이다. 모든 값이 구간 내에 있음을 확인할 수 있다. bartMachine에서 제공하고 있는 변수의 중요도는 inclusion proportion으로 각 tree에서 특정 변수가 선택된 비율(선택노드수/전체노드수)을 계산하여 평균을 취한 것이다(Figure 15). 중요도의 순서는 randomForest의 결과와는 다소 다른 점들이 있다. 가장 중요한 변수는 hipcirc이며 waistcirc가 그 다음을 차지하고 있다. 또한 kneebreadth가 anthro3a보다 높은 중요도를 보이고 있으며 전체적인 중요도의 차이가 randomForest에서 만큼 크게 나타나지 않는다. 즉, anthro3a와 kneebreadth의 중요도가 hipcirc의 70% 정도로 나타나고 있다.
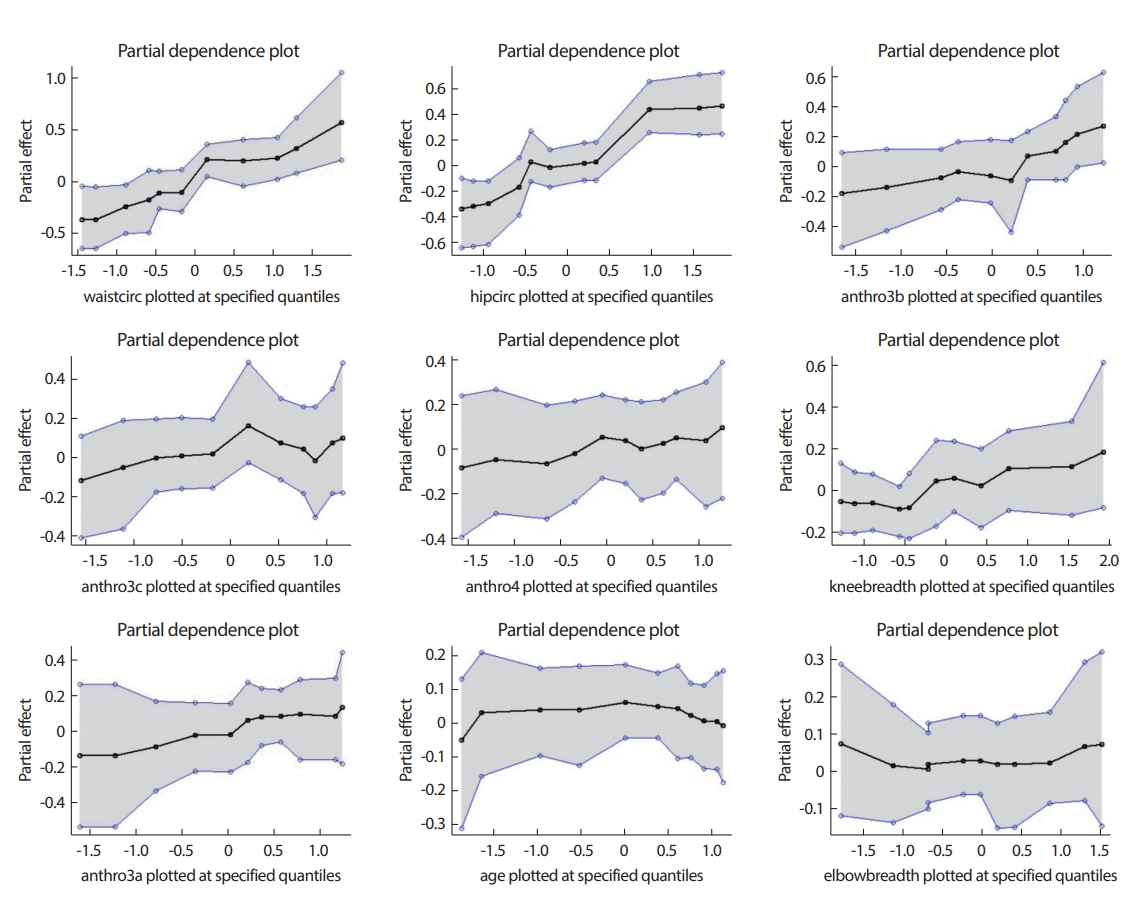
BartMachine에서는 지정 변수 이외의 나머지 변수들이 고정되어 있을 때의 반응변수와의 관계를 보여주는 partial plot을 제공하고 있다 (Figure 16). 선형관계와 같은 특정 패턴은 지정 변수의 중요도를 나타낸다. 대부분 중요도에서 보여준 순서대로 DEXfat과의 연관성을 보여주고 있으나 anthro3a의 경우 낮은 중요도임에도 DEXfat과의 선형관계를 보여주고 있다.
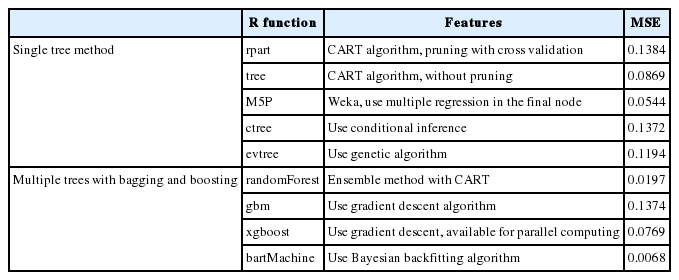
Table 2는 R에서 제공하고 있는 다양한 함수에 대한 설명과 이들을 DEXfat을 추정한 결과를 정리한 것이다. bartMachine이 가장 낮은 MSE를 보이고 있으며 randomForest와 M5P 또한 0.0758의 MSE 값을 갖는 선형회귀보다 좋은 결과를 보이고 있다. xgboost와 tree는 선형회귀와 비슷한 성능을 보이고 있다.
연구 결과
회귀나무모형 추정 결과 시각화 활용 방안
서울특별시 종합병원 병상 수 예측 시각화
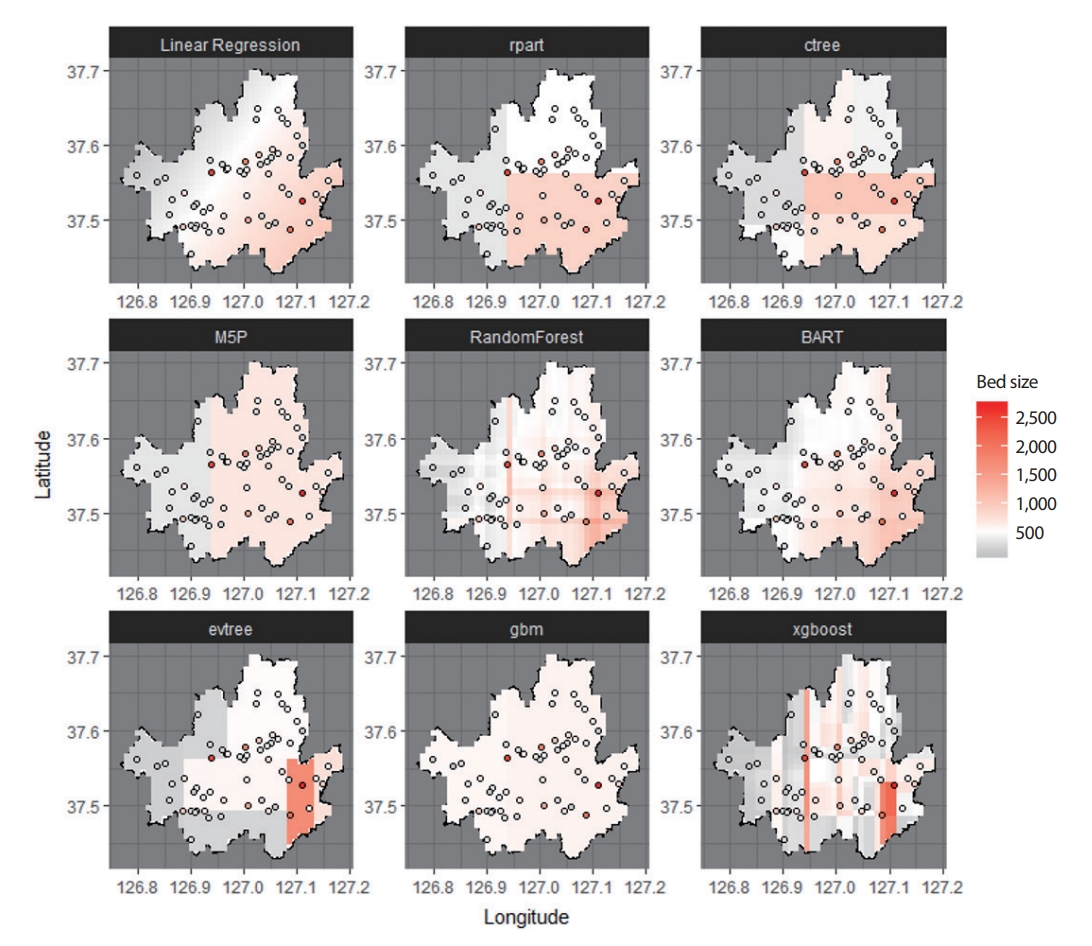
회귀나무기법의 분할과 예측 과정을 서울특별시 내의 종합병원 병상 수를 위도, 경도에 따라 시각화하였다. 데이터는 서울열린데이터 광장의 서울특별시 종합병원 정보를 이용하였다. 서울시 안의 병상 수가 가장 많은 병원 5곳은 서울아산병원, 신촌세브란스병원, 삼성서울병원, 서울대학교병원, 서울성모병원이었다(2018년 11월 기준). 다양한 회귀나무 모델을 학습시키기 위하여 서울시 내 57개 종합병원의 위도, 경도에 따른 위치를 설명변수로 사용하였고 환자 병상 수를 예측변수로 활용하였다. 학습된 회귀나무 검증을 위해 서울시의 위도, 경도 범위를 40개의 격자로 나누어 입력으로 활용하여 예측값을 검증하였다. Figure 17은 9개의 모형 추정결과를 시각화한 것이다. 서울시 지도 위에 표기된 점은 57개의 병상 수를 의미한다. 각 격자 영역에 따른 예측 값은 회색일수록 상대적으로 적은 병상 수를 나타내고, 흰색에 가까울수록 평균에 가까운(약 500개) 병상 수를 나타낸다. 또한 붉은색일수록 상대적으로 많은 병상 수를 의미한다. rpart의 경우 서울아산병원, 신촌세브란스병원, 삼성서울병원, 서울성모병원이 한 노드에 묶인 것을 확인하였다. 또한 randomForest를 사용하여 실험한 결과, 많은 병상 수를 보유한 대형병원(서울아산병원, 신촌세브란스병원, 삼성서울병원, 서울성모병원, 서울대학교병원 등)이 위치한 위도, 경도가 붉게 나타나는 것을 확인하였다. 이를 통하여 병상 수가 많은 종합병원들은 서울의 남동쪽에 밀집해 있고, 서울의 북서쪽에는 상대적으로 병상 수가 적은 종합병원들이 있음을 파악할 수 있다.
예측 모형별 성능 평가를 위한 시각화
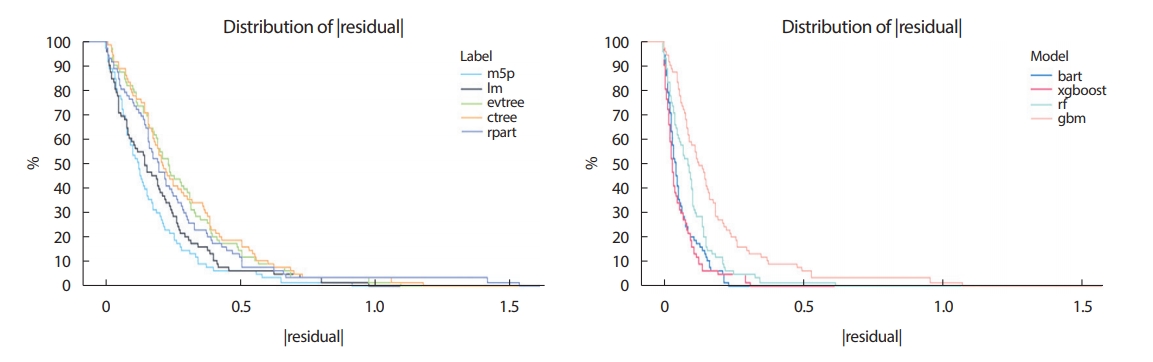
앞서 다루었던 bodyfat 자료의 DEXfat 예측을 위해 다양한 회귀나무를 사용하여 모델을 만들고 DALEX패키지[33]의 variable_response 함수와 auditor패키지[34]의 model_residual함수 등을 사용하여 단일나무모형과 다중나무모형을 구분하여 이 모형들의 성능을 비교하였다. 잔차를 시각화하면 모델의 예측 정확도가 떨어지는 지점의 식별이 용이해진다. Figure 18은 모델링 후 계산되는 잔차들의 절댓값을 시각화한 그림으로, 왼쪽 그림은 단일나무모형의 결과를, 그리고 오른쪽 그림은 다중나무모형의 결과를 나타낸다. 다중나무모형이 전반적으로 단일나무모형보다 빠르게 감소하는 양상을 보인다. 단일나무모형에서는 M5P가 선형회귀(lm) 방법보다 빠른 감소폭을 보인다. 다중나무모형에서는 barMachine과 xgboost가 초기에는 비슷하게 빠르게 감소하지만, xgboost는 잔차의 절댓값이 큰 관측치들이 있음을 확인할 수 있다. Figure 19에서는 잔차의 절댓값으로 상자그림을 그린 결과이다. 빨간점은 잔차 제곱 평균의 제곱근값(Root mean square of residuals)을 표시한 것이다. 이 빨간점의 값을 기준으로 크기 순으로 모형이 나열되어 그려졌고, 이 자료에서는 단일나무모형 중에서는 M5P가 잔차의 중앙값과 평균이 모두 가장 낮았고, 다중나무모형에서는 bartMachine이 잔차 제곱 평균의 제곱근값이 가장 낮았다. 잔차의 중앙값은 xgboost가 더 낮지만, 잔차도에서 이 모형의 꼬리 부분에 더 큰 관측치가 있었기에, 분포에서 bartMachine 모델에 비해 더 큰 잔차가 있을 수 있다. 이러한 그림을 이용하면, 잔차가 모델에 따라 어떻게 비슷하고 다르게 행동하는 지를 종합적으로 파악하는 것이 가능해진다.
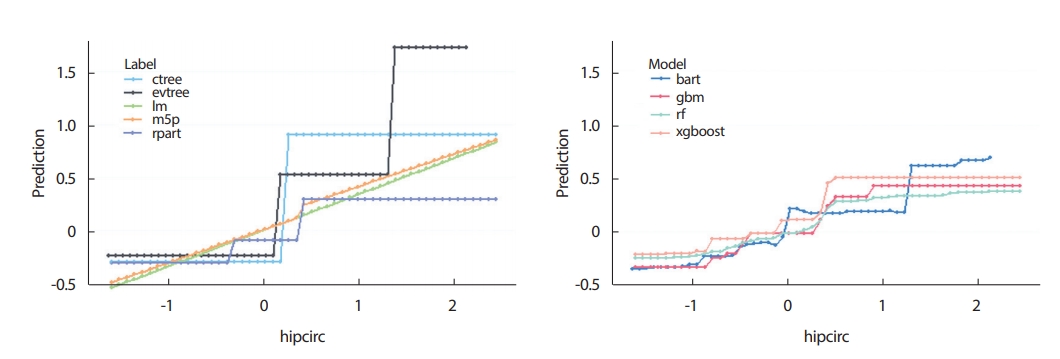
단일 변수가 각 예측 모형들 내에서 추정치에 영향을 어떻게 다르게 미치는지를 보기 위해 모든 예측모형에서 중요변수로 나타나고 있는 hipcirc변수와 waistcirc변수에 대한 부분 의존도 그림(Partial Dependence Plot [26])을 이용하였다. 이는 각 추정 모형에서 나머지 설명변수들이 평균값으로 고정되어 있을 때의 특정 변수와 추정값 간의 관계를 나타낸 그림이다. Figures 20, 21은 DEXfat을 예측하는 데 hipcirc변수와 waistcirc변수 각각이 각 모형들의 결과에 미치는 영향을 시각화한 것이다. 두 변수 모두 값이 커질수록 전반적으로 예측값도 함께 커지는 양상을 보이고 있으며, 단일나무모형보다 다중나무모형이 복잡한 형태로 움직임을 알 수 있다. 단일나무구조 중에서 M5P는 선형회귀모델처럼 양의 기울기를 가지는 선형 라인이 보이는 것을 시각적으로 파악할 수 있다.
임상자료를 이용한 회귀나무모형의 예측력 비교
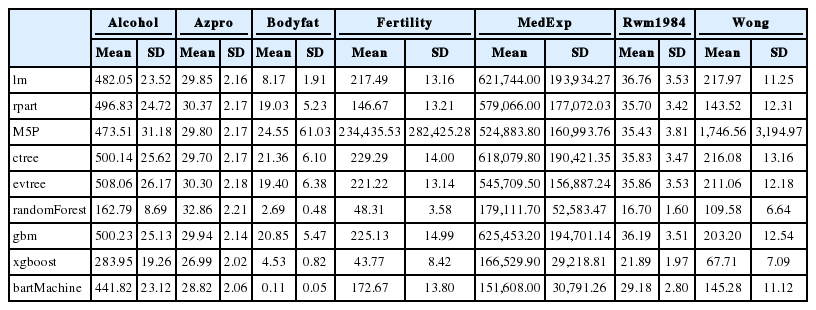
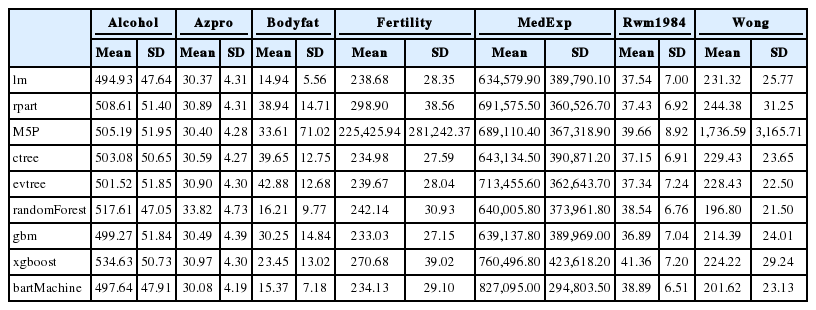
회귀나무들의 예측력을 비교해 보기 위하여 다양한 보건관련 자료를 이용하였다. 사용한 자료의 출처와 자료의 특징들은 Table 3에 정리되어 있다. 각 자료에 대하여 2/3의 학습 데이터와 1/3의 테스트 데이터로 나눈 후 학습 데이터를 이용하여 모형을 추정하고 이를 이용하여 학습 데이터와 테스트 데이터 각각에서 예측력의 척도인 MSE를 구하였다. 학습데이터와 테스트 데이터로 나누어 모형을 추정, 각각의 MSE를 구하는 과정을 100번 반복하여 계산한 MSE들의 평균과 표준편차가 Tables 4, 5에 정리되어 있다.
학습 데이터의 결과를 방법론별로 살펴보면, 7개의 데이터 모두에서 선형회귀분석(lm)보다 bartMachine과 xgboost의 MSE의 평균이 낮음을 확인할 수 있었다. randomForest의 경우도 azpro데이터를 제외하면 모두 선형회귀분석보다 MSE가 낮았다. 데이터 별로 결과를 보면, MedExp데이터의 경우에는 GBM방법론을 제외, Wong데이터에서는 M5P를 제외하면 모든 회귀나무 방법론이 선형회귀방법론보다 MSE가 낮았다. rwm1984데이터에서는 모든 회귀나무 방법론이 MSE가 선형회귀보다 좋았다. 반면에 테스트 데이터에서는 다른 양상이 보인다. alchol데이터의 경우 선형회귀 모형이 MSE가 가장 낮았고, Wong데이터에서는 rpart와 M5P가 선형회귀모형보다 MSE가 높아졌다. xgboost 방법론은 Wong데이터를 제외하면 모두 선형회귀모형보다 MSE가 높다. 또한 대부분의 데이터에서randomFroest와 xgboost방법은 학습 데이터에 비해 높은 테스트 데이터의 MSE를 보이고 있다. 이를 이용해 두 방법에서는 과적합 문제가 발생하였음을 유추할 수 있었다.
고찰 및 결론
본 논문에서는 R에서 제공되고 있는 다양한 형태의 회귀나무모형 추정 함수를 살펴보았다. 이들로부터 얻은 결과를 시각화하여 분석 결과에 대한 이해와 자료에 대한 통찰력을 얻을 수 있는 시각화 방법들을 제시하고자 하였다.
사용한 회귀나무모형들은 크게 단일 나무방법과 다량의 나무방법으로 나눌 수 있다. 단일 나무 모형은 추정의 안정성은 떨어지지만 해석이 직관적으로 매우 용이하다는 장점이 있다. CART의 이진나무모형 알고리즘은 rpart에 구현되어 있고 적합된 나무 결과의 가독성을 높이기 위해 rpart.plot과 rattle패키지가 개발되어 심미적인 나무구조를 표현할 수 있다. M5P는 Rweka패키지로 구현되어 있고 각 최종 노드에 대한 회귀 계수를 파악할 수 있다. ctree함수는 조건부 추론을 이용한 나무구조를 추정하기 위한 알고리즘을 구현해 놓은 함수로, party 패키지 안에 구현되어 있다. 자료 공간을 분할하여 국지적인 최적화를 하는 것이 아니라 나무모형 전체를 고려하기 위해 진화알고리즘을 이용한 나무는 evtree패키지에 구현되어 있다. 다중 나무란 모형 추정이 불안정한 나무구조의 단점을 보완하기 위해 배깅방법과 부스팅 방법 등을 이용한 앙상블 기법의 나무를 뜻한다. 배깅을 이용한 randomForest 패키지, 부스팅을 이용한 그래디언트 부스팅(gbm)과 이를 분산 환경에서 실행할 수 있도록 구현한 xgboost, 배깅과 부스팅을 모두 이용한 bartMachine을 이용하여 다중나무알고리즘들도 함께 비교하였다. 각 모형별로 해석을 위해 제공되는 시각화 함수들을 사용하여 독립변수들의 영향을 해석하였다.
예측값의 형태를 보기 위해 서울특별시 종합병원 병상 수 예측을 시각화하기 위하여 위도, 경도의 정보를 사용하였고, 이를 이용하여 높은 병상수를 보유한 병원들을 잘 구별해내는 지를 지도로 표현할 수 있었다. 적합 정도 및 성능 평가를 파악하기 위해 bodyfat 자료를 이용하여 모형별 잔차도 그림을 그려 잔차가 모델에 따라 어떻게 다른지 살펴보았다. 또한 단일변수의 모형별 부분 의존도를 이용하여 각 변수가 예측 모형들 내에서 추정치에 영향을 어떻게 다르게 주는지 살펴볼 수 있었다. 또한, 회귀나무모형들 중 8가지의 모형을 이용하여 7가지의 임상 데이터에 적용하여 그 성능을 MSE값 기준으로 모형을 평가하였다. 그 결과 다중나무 모형들 중 randomForest와 xgboost는 과적합 문제가 발생하여 적합도는 높으나 예측력이 떨어짐을 한 눈에 볼 수 있었다.
본 연구에서는 R로 개발되어 있는 패키지에 국한된 연구를 진행하고 이를 시각화하였다. 그러나 R 이외의 다른 언어로 개발되어 있는 소프트웨어의 분석 결과도 유사한 방법으로 시각화하여 결과를 비교해 볼 수 있다. 본 연구를 통하여 자료 분석에서 시각화의 중요성을 다시 한 번 확인할 수 있고, 특히 나무구조모형의 분석 결과를 다양한 방법으로 결과의 특성을 살려 시각화함으로써 자료에 대한 통찰력을 얻을수 있음을 확인하였다.
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (2018R1A2B6001251).
Notes
No potential conflict of interest relevant to this article was reported.