다중 커널을 이용한 파킨슨 환자로부터 보행 동결 진행까지의 페널티 콕스 회귀 분석
Penalized Cox Regression Analysis from Parkinson Disease to Freezing of Gait Using Multiple Kernels
Article information
Trans Abstract
Objectives
The objective of this study was to investigate complex non-linear associations of multiple genetic and brain imaging factors and the interactions of the two factors with the risk of gait freezing for patients with Parkinson's disease (PD).
Methods
We employed a penalized kernel machine Cox proportional hazard regression model. Multiple kernels were created to account for multiple genetic factors and their interactions with brain imaging factors, and we identified significant elements using the group lasso penalty. We applied the proposed method to Parkinson's Progression Markers Initiative (PPMI) data.
Results
We identified LRRK2 genes and the volume of six regions of interest in brain interacting with COMT, GBA, LRRK2, and SNCA genes that are associated with the occurrence of freezing of gait for PD patients.
Conclusions
It was found that there is evidence of gene-brain interactions in freezing of gait. The proposed penalized Cox model using the kernel machine method enables us to identify the nonlinear relationship between genetic and neuroimaging factors and the occurrence of neurodegenerative diseases.
서 론
파킨슨병(Parkinson's disease)은 흔히 발견할 수 있는 신경퇴행성 질환 중 하나다[1]. 주로 노년층에서 발생하는 질환이며 뇌 흑질(substan-tia)의 신경세포가 소실되며 60% 이상 소실되면 명확한 증상이 나타난다. 주요 증상으로 운동성 증상과 비운동성 증상이 있는데 운동성 증상은 떨림, 강직, 운동 완화증, 운동 불능 등이 있다. 보행 동결(freezing of gait)은 파킨슨병이 많이 진행되면 나타나는 증상 중 하나인데, 급격한 몸의 변화가 존재할 때 행동을 제때 하지 못하고 느리게 반응하는 특징을 가지고 있다[2]. 비 운동 증상은 인지 기능 저하, 수면 장애, 배뇨 장애, 우울증 등이 있다.
최근 사회 고령화가 진행되면서 파킨슨병 환자들이 점차 증가하고 있다. 1990년도에 약 3백만 명의 환자가 존재했으며 추후 2040년이 되었을 때 4배 이상의 파킨슨병 환자가 존재할 것이라 예상해왔다[3]. 그리고 산업화가 진행된 국가에서 유병률을 조사했을 때 전체적인 사람들을 대상으로 유병률이 0.3%인 반면 60세 이상인 사람들을 대상으로 계산한 유병률은 1%에 도달하였다. 심지어 80세 이상인 사람을 대상으로 유병률을 계산했을 때 3%가 넘는 현상이 발생하였다[1].
그러나 흔히 발견되는 질병임에도 불구하고 발생하는 정확한 원인은 아직 발견되지 않았다. 간접적인 원인으로 흡연, 카페인 섭취 등의 요소가 있으며[4], 가족력 또한 파킨슨병의 발병 원인 중 하나로 드러나 있다[5]. 본 연구는 파킨슨병의 여러 요인 중에 유전적 요소에 초점을 맞췄으며, 또한 유전적 요인이 다른 요인과 교호작용을 발생시켜 파킨슨병에 영향을 주는지에 대한 분석을 진행하였다.
유전적 요인과 환경 요인에 대한 연구들은 여러 차례 진행되어 왔다. 대표적으로 Marceau et al. [6]의 연구는 커널 머신 모형을 활용한 유전자 및 환경 요인의 교호작용과 유전자 내의 교호작용에 대한 연구이며, Lin et al. [7]의 연구는 일반화 선형모형을 활용해 유전적 요인과 환경 요인, 단일 핵산 염기 요인과 환경 요인에 대해 각 교호작용이 유의미한지 찾아내는 연구이다. 그러나 파킨슨병이 있는 환자들의 보행 동결까지의 유전적 요인을 탐색하는 연구는 비교적 최근 시작되었다. 대표적으로 Radojević et al. [8]은 보행 동결 증상의 발생과 관련된 유전자를 찾기 위해 파킨슨병을 투병하고 있는 환자들 중 보행 동결 비발생 환자와 보행 동결 발생 환자의 유전자 대조를 통해 유의미한 유전자를 찾아내는 연구를 진행하였다.
유전자와 자기공명영상(magnetic resonance imaging, MRI)에서 관심 지역(region of interests, ROI)에서 추출한 뇌의 부피에 대한 교호작용의 연구 또한 최근 들어 시작하였다. 대표적으로 Bi et al. [9] 연구에서 가중치를 적용한 랜덤포레스트를 활용한 경도 인지 장애를 예측할 수 있게 유전자 및 관심 지역의 원소 하나씩 쌍을 만들어 매트릭스(matrix)를 생성하여 연구를 진행하였다.
그러나 보행 동결 발생에 끼치는 유전적 요인 그리고 유전적 요인과 교호작용이 있는 뇌영상학적 요인을 찾아내는 연구가 아직 진행되지 않았다. 본 연구는 파킨슨병 환자의 보행 동결 증상에 영향을 주는 어떤 유전적, 뇌영상학적 요인이 있는지 찾고자 한다. 하나의 유전자에 속해 있는 단일 핵산 염기 다형현상(single nucleotide polymorphism, SNP)들의 연관성과 반응변수와의 비선형적 관계성을 고려하여 여러 유전자에 대응되는 다중 유전자 커널 함수와 관심 지역의 뇌 부피와 유전자의 교호작용에 대응되는 교호작용 커널 함수를 생성하여 콕스 비례위험 모델에 적용하였다. 데이터는 파킨슨병 환자들에 대한 오픈소스인 PPMI (Parkinson's Progression Markers Initiative data; https://www.ppmi-info.org/)를 활용하였다.
2절에서 생존분석 모형인 콕스 비례 위험 모형 및 SNP 데이터에 맞는 IBS 커널을 소개하며 이를 활용해 교호작용 커널을 만들고 적용하는 과정을 설명하고 3절에서 실제 데이터인 PPMI 데이터를 적합시켜 결과를 보일 것이며 4절에서 본 연구에 대해 시사할 점과 한계에 대해 간략히 고찰 및 논의하고자 한다.
연구 방법
연구대상 및 자료수집
본 연구는 PPMI에서 제공하는 오픈 데이터를 활용하였다. PPMI는 전향적 코호트로 전 세계의 약 50개의 장소로부터 참가자 모집을 2010년에 시작하였으며 등록 중단 뒤에 연구가 확대되어 2020년 이후 재모집을 적용하여 약 4,000명의 파킨슨병 환자군, 대조군 피실험자를 수집하였다. 참가자에 대하여 전구증상에서 중증까지 파킨슨병의 모든 단계에 걸쳐 임상적 특징, MRI와 같은 영상 결과, 생물학적 및 유전적인 마커 등의 데이터를 제공한다.
파킨슨병 계측척도(Unified Parkinson's Disease Rating Scale, UPDRS)의 세 번째 파트 중 보행 동결의 정도를 나타내는 변수(NP3FRZGT)가 1보다 크면 보행 동결이 발생한 환자로 분류하였고, 0의 값을 가지는 경우 보행 동결이 발생하지 않은 환자로 분류하였다. 또한 진단 기록을 활용해 보행 동결이 발생한 환자는 처음 파킨슨병을 진단받은 시점부터 보행 동결이 발병한 시점까지의 기간을, 보행 동결이 발생하지 않은 환자는 관측 종료 시점인 2022년 6월로부터 가까운 마지막 진단 날까지의 기간을 1달 기준으로 수치화한 값을 생존 시간으로 정의하였다.
다음으로 보행 동결에 영향을 미치는 요소 중 유전적 요소로 SNP 데이터를 이용하였고, MRI를 활용해 관심 지역의 부피를 추출했으며, 두 요소를 결합한 교호작용을 생성하였다. 또한 인구통계학적인 요소 중 나이와 성별을 추가로 고려하였다.
인구통계학적 자료
기본적으로 제공해주는 인구통계학적 자료 중 나이는 관측 기간이 시작된 시점의 나이를 이용하였다. 또한 성별을 여성이면 0의 값을, 남성이면 1의 값을 갖도록 표기하였다.
자기공명영상의 관심 지역
MRI 영상 데이터를 선택할 때 환자들이 최초로 촬영했던 시점의 데이터를 선택했으며, T1 강조영상(T1-weighted MRI)을 사용하였다. 이 영상은 자화 준비된 빠른 기울기 에코 이미징 시퀸스를 사용한 1.5 또는 3-Tesla 스캐너를 사용해 획득하였다. 일반적인 MRI 매개변수는 반복 시간 = 5-11 ms; 에코 시간 = 2-6 ms; 슬라이스 두께 1-1.5 mm; 슬라이스 간 간격 0 mm; 복셀 크기 1×1×1.2 mm; 매트릭스 최소 256×160을 사용하고 있다. 이 MRI 데이터로 특별 분할 도구인 Free-Surfer (version 6.0, http://surfer.nmr.mgh.harvard.edu)를 이용해 각 피실험자의 좌뇌와 우뇌 각각 관심 지역의 피질의 부피를 추출하였다. 또한 피실험자 마다 뇌의 총 부피가 다를 수 있으므로 [(각 관심 지역의 볼륨/전체 뇌의 볼륨)×100]을 통해 정규화하였다. 또한 [(좌뇌의 부피+우뇌의 부피)/2]로 피실험자마다 좌뇌와 우뇌의 같은 부위의 평균을 사용하였다[10].
단일 핵산 염기 다형현상
SNP는 DNA 서열에서 일어나는 단일 염기의 변이를 뜻한다. 따라서 SNP 데이터는 SNP 마커의 위치별로 두 개의 위치에 대한 변이 값을 가지게 된다. 변이가 일어나지 않은 정상 인자를 우성인자라 표기했을 때, 모두 우성 SNP 마커를 보유하면 0의 값을, 우성 1개, 열성 1개 SNP 마커를 보유하면 1의 값을, 모두 열성 SNP 마커를 보유하면 2의 값을 가지는 데이터 행렬을 활용하였다. 여기서 우성 SNP 마커는 변이가 존재하지 않은 염기를 뜻한다. 프로그램 BCFtools를 이용하여 SNP 데이터를 추출했으며 PLINK (v1.90b52) 프로그램을 통해 이분 PLINK 형태 데이터 변형을 진행하였다. 또한 제노타이핑 퀄리티 스코어를 이용해 최소 20인 데이터만을 추출하였다. 유전자의 종류는 파킨슨병 발병을 유도하는 유전자 중에서 SNCA, GBA, LRRK2 유전자를 선정하였고[4], 보행 동결 증상이 발생하는 데 영향을 미치는 COMT 유전자를 본 연구에 포함하였다[8].
콕스(Cox) 비례위험 모형
생존분석은 생존함수 또는 위험함수를 추정하는 방법론을 연구하 는 분야이다. 위험함수h(t) 는 ‘순간위험률’이라고도 하며, 시점까지 생 존한 환자가Δt 시점 이후 사망하는 확률을 나타낸다.T가 연속형 확 률변수인 생존 기간이라 할 때, 순간위험률은 다음과 같이 기술된다.
Cox [11] 회귀모형은 위험함수를 기반으로 질병 발병 여부와 관련된 설명변수들이 존재할 때 해당 변수들이 어떤 영향을 주는지 알아보기 위해 사용하는 대표적인 생존분석 모형이다. 이 모형은 데이터의 특성을 잘 반영하지만 생존 시간 분포를 가정하지 않는 준 모수적 특징을 가지고 있다.
본 연구에서n 은 피실험자의 수,M은 유전자의 수, 그리고Q는 관심 지역의 수라고 표기하였다:n명의 환자가 존재하고p개의 설명변수가 존재할 때,i(1 ≤ i ≤ n)번째 환자의 설명변수 관측 값을 zi = (zi1, zi2, … zip)라고 하면 시점에서의 모형식은 다음과 같다.
여기서 β = (β1,β2, …, βp)는 회귀모형의 계수 값을 뜻하며, 모든 설명변수가 기본값을 가지게 되면h0(t) 로 표시할 수 있는데 이 함수 를 기저 위험함수라고 한다. 콕스 비례위험 모형을 추정할 때 가능도 비 함수를 활용해 추정하며 가능도비 함수는 다음과 같이 유도된다.
커널 변수 생성
SNP 데이터를 활용하는 본 연구에서 같은 유전자의 위치마커끼리 상관관계가 존재하기 때문에 다중공선성이 발생할 수 있다. 또한 콕스 비례 위험 모형에서 보면 선형 관계로 회귀 적합이 진행되는 것을 확인 할 수 있다. 비선형 관계와 동일 유전자의 위치마커 간의 상관관계를 동시에 고려하기 위해 커널 머신 회귀 모델을 콕스모형에 적용하였다. SNP 데이터는 우성인자 개수에 따라 0, 1, 2 값을 가질 수 있기 때문에 일반적으로 알려진 다항 커널(polynomial kernel), 가우시안 커널(Gaussian kernel) 등 연속형 변수를 활용하기 위한 커널은 사용하지 못한다. 따라서 다음과 같이 0, 1, 2 값을 가졌을 때 사용할 수 있는 IBS 커널을 활용하였다. IBS 커널은 각 SNP 마커의 우성인자인 염기서열과 대조하 여 우성인자와 같은 염기를 가졌을 때 가중치를 부여해 유전적 유사성 을 정량화하는 커널이다[6]. m번째 유전자 커널을 생성할 때 만들어지는n × n 크기의 커널 행렬을 kGm 이라 정의하며, Gi 를 원 데이터에서 SNP 데이터 행렬의 번째 환자의 SNP 데이터 벡터로 표기했을 때 식은 다음과 같다.
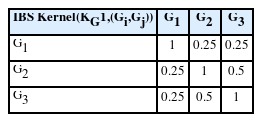
Lm은m 번째 유전자 마커의 집합을 뜻하며|Lm|은 Lm 의 크기를 의 미한다.i번째 환자와j 번째 환자의 유전자별 SNP 마커에 대해 SNP 마 커 행렬의 값이 같으면 2의 가중치를, 값의 차이가 1이면 1의 가중치를 부여하여 한 유전자에 포함되는 SNP 마커의 가중치에 대한 총합을 구한 뒤 유전자에 포함된 총 SNP 마커의 개수에 2를 곱하여 나누어진 값을 가진n × n 행렬을 산출하였다. 예를 들어, 같은 유전자에 속한 2개의 SNP 데이터, SNP1과 SNP2가 있다고 하자. 이때, 3명의 환자에 대한 유전자 Gi 값이 각각 G1 = (2,0), G2 = (0,1), G3 =(1,2) 라고 한다면
한편 일반적으로 사람들은 유전자에 따라서 신장, 체중부터 신체 기관의 형성까지 영향을 받는다. 또한 사람은 뇌를 갖고 태어나며 뇌를 구성하는 관심 지역들의 부피 또한 유전자로부터 영향을 받는다. 따라 서 유전자와 관심 지역의 부피 사이에서 교호작용이 존재할 수 있다. 따라서 IBS 커널을 활용해 유전자 커널 행렬을 활용해 교호작용 커널 을 생성하였다. 유전자 커널 kG1 부터 kGM 까지의 n × n 커널 행렬과 관 심 지역 하나하나의 부피에 대해 대각행렬을 만들어 유전자 커널 행렬 의 양옆으로 곱해 교호작용 커널을 생성하였다[6]. 행렬B 를 관심 지역 의 부피에 대한 n × Q 행렬이라 했을 때, V = diag (Bq) 의 대각행렬 을 생성해 다음과 같이 표현하였다.
연속형 변수인 관심 지역의 부피에 대한 행렬 B 의 특성을 가진 행 렬Vq 를 양쪽에 곱해 kGm,Vq 을 생성하였다. 유전자 종류의 개수인 M 과 관심 지역의 개수 Q 를 곱한 M × Q 개의 교호작용 커널을 생성한 후 본 연구의 교호작용 요소로써 활용하였다.
다중 커널을 활용한 콕스 비례위험 모형
유전자 커널 및 교호작용 커널과 인구통계학적인 요소와 관심 지역 에 대한 부피를 설명변수로 활용해 다음과 같이 표현하였다.
여기서 Xi 는 i 번째 환자의 인구통계학적 요인 벡터이고, Bi 는 i 번째 환자의 관심 지역의 부피를 나타낸다. 또한 B = (B1, B2, … BQ) 을 의 미하며, αmj 와 Θmq,j 는 각각 유전자 커널, 교호작용 커널에서 생성된 커 널 변수의 계수를 뜻한다. 각 커널의 계수를 하나의 벡터로 표현해 각각 α =(α11,…,α1n,α21,…,αMn)', Θ = (Θ11,1,…,Θ11,n,Θ12,1,…,ΘMQ,n)'로 표기한다. 따라서 콕스 비례 위험 모형은 아래 식과 같이 표현할 수 있다.
또한 가능도비 함수는 다음과 같이 표현할 수 있다
그룹 라쏘 페널티
기존의 가능도비 함수를 그대로 이용해 추정하게 되면 환자의 수보 다 속성의 수가 훨씬 큰 형태로 모형 적합이 될 것이다. 이 모형을 그대 로 사용하게 된다면 피실험자의 수를 뜻하는 행의 개수보다 변수를 뜻하는 열의 개수가 훨씬 많을 것이다. 이에 따라 적합 자체가 진행되 지 않을 수 있다. 따라서 이러한 현상을 해결하기 위해서 변수 선택 과 정이 필요하다. 그러나 잘 알려진 선택법 중 단계적 선택법, 전진 선택 법 등 p-값을 활용해 변수를 선택하는 방법은 많은 변수를 계산하기에 시간과 비용을 많이 소비해야 한다는 단점이 있다. 따라서 이를 보완 하기 위해 본 연구에서는 라쏘(least absolute shrinkage and selection operator, LASSO) 방법을 선택하였다. 라쏘 방법은 가능도비 함수 등 추정함수에서 각 계수의 절댓값의 총합을 더해 계수의 크기 또한 최 소로 줄여 0에 가까워지는 값을 0으로 만들기 때문에 변수 선택에 있 어서 큰 안정성과 정확성을 준다[12]. 절댓값을 이용해 식을 구성하게 되며 한번 미분하였을 때, 꺾이는 부분에서 0으로 만들어준다. 따라서 페널티를 강하게 부과하며 영향이 큰 계수들만 선택된다. 그러나 현재 의 요인 행렬은 한 커널로부터 생성된 변수들이 많기 때문에 각 변수 를 하나의 변수로 동일하게 부과하기 어렵다. 또한 커널에서 나온 변수 중에서 일부가 선택된다고 하더라도 해석이 어려울 수 있는 단점이 있 다. 따라서 이를 해결하기 위해 한 커널에서 나온 n 개의 변수를 하나의 그룹으로 지정해 같은 크기의 페널티를 받아 그룹 채로 선택하게 만드 는 그룹 라쏘 방법을 본 연구에서 활용할 것이다[13]. 로그 가능도비 함수 ln (β,α,Θ,h0(·)) = log (Ln(β,α,Θ,H0(·))) 와 그룹 라쏘 의 식을 추가해 목적 볼록 함수를 아래와 같이 생성하였다.
λ는 그룹 라쏘에서 조절할 수 있는 조율 모수(hyperparameter)이며 dfm, dfmq 는 각각의 유전자 커널, 교호작용 커널에서 그룹에 대한 조 정 변수다. 각 유전자 커널 및 교호작용 커널에서 각 커널 내 유의미한 변수의 개수가 다르기 때문에 특잇값 분해를 활용해 그룹의 길이를 반 영하였다. 또한 ||·||2 는 유클리디안 거리(Euclidean distance)를 의미한다. 본 연구에서는 그룹에 대한 조정변수로 각 커널에서 특잇값 분해를 진행한 뒤에 고유벡터의 크기가 아주 작은 상수 의 임계값보다 큰 고윳 값의 개수를 반영하였다. 이에 따라 그룹 단위로 라쏘 방법이 이루어 지며 한 커널그룹이 제외될 때 그 커널그룹에 속하는 변수들 또한 모 두 제거된다. 따라서 커널 단위로 묶여서 라쏘 방법으로 선택되므로 해석에 대한 용이함과 불필요한 변수를 더 빠르게 없앨 수 있는 장점 이 있다.
연구 결과
분석 데이터
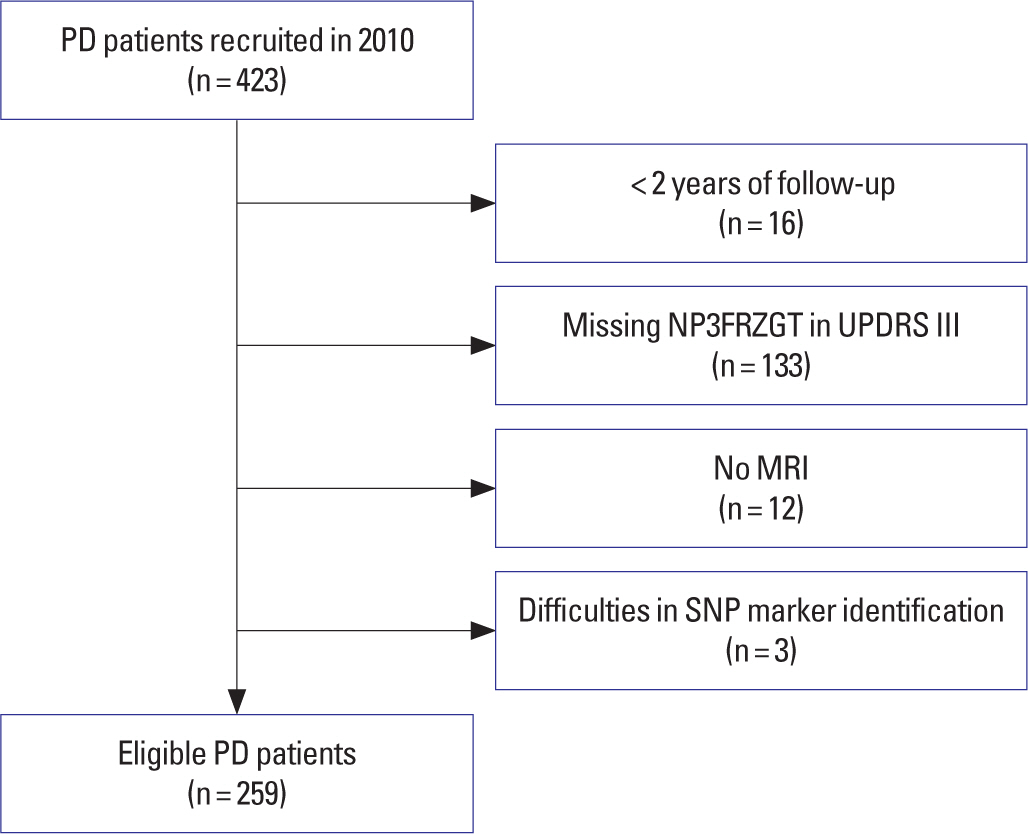
본 연구는 PPMI 코호트에서 2010년에 모집된 조기 파킨슨병 환자 423명을 대상으로 분석을 실시하였다. 관측 기간이 2년 미만인 경우 (n = 16), 파킨슨병 계측척도 세번째 파트(UPDRS III) 중 보행 동결 관 련 변수(NP3FRZGT)가 존재하지 않는 경우(n=133), MRI가 존재하지 않은 경우(n = 12), SNP를 식별할 수 없는 경우(n = 3)를 제외한 최종 259명을 대상으로 실험을 진행하였다(Figure 1).
뇌 부피데이터는 뇌의 피질을 34개 관심 지역으로 세분화하여 각 관 심 지역에 대한 부피로 구성되었다. SNP 데이터는 네 가지 유전자 SNCA, GBA, LRRK2, COMT에 속하는 SNP로 구성되었고, 259명의 환자에 대해 모두 같은 값을 가진 SNP가 존재했기 때문에 이러한 SNP 종류 는 배제하고 분석을 진행하였다. 총 5개의 SNCA 유전자에서 3개를 제 외한 rs356181, rs3910105를 포함하였고 총 6개의 GBA 유전자에서 2개 를 제외한 rs421016, rs76763715, rs75548401, rs2230288을 포함하였으며 총 7개의 LRRK2 유전자에서 4개를 제외한 rs76904798, rs33949390, rs34637584을 포함하였다. 총 11개의 COMT 유전자에서는 환자 모두 같은 값을 가지는 SNP가 없었으므로 11개의 rs737866, rs174674, rs5993883, rs740603, rs165656, rs6269, s4633, rs2239393, rs4818, rs4680, rs165599를 포함하였다. 두 요소 ROI와 SNP를 각각의 변수로 포함하 여 최종 데이터를 구성하였다.
네 가지 인구통계학적, 유전자 커널, 관심 지역의 부피, 교호작용 커 널 변수를 모두 합쳐 총 259행 36,296열의 데이터가 생성되었다. 커널 의 총 개수는 유전자 커널 4개와 교호작용 커널인 4×34=136개의 커 널로 140개의 커널이 적용되었다. 분석은 프로그램 R (version 4.2.1)을 활용하였다.
연구대상자의 기술적 특성
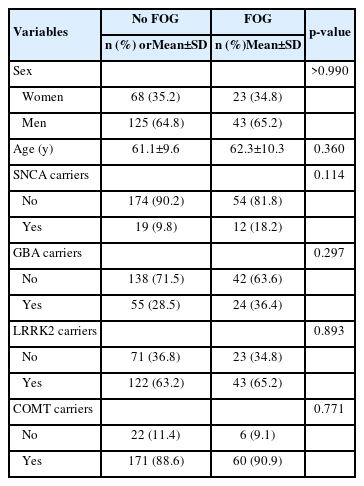
보행 동결이 발생한 집단과 발생하지 않은 집단의 나이와 성별, 네 가지의 유전자에 대해 차이가 존재하는지 t-검정 방법과 카이제곱 검 정을 이용하여 비교한 값을 Table 2에서 확인할 수 있다. 나이에 대한 p-값은 0.36의 값을 가지며 성별에 대한 p-값은 1에 가까운 값을 가진 다. 이를 통해 나이와 성별로 인해 두 집단의 차이가 설명되지 않는 것 을 확인하였다. 또한, SNCA, GBA, LRRK2, COMT 유전자 보유자와 비보유자의 보행 동결 발생 차이가 없었다. 마지막으로 뇌 관심 지역 부피에 대해 FOG 발생 차이가 있는지 확인했을 때 Inferior Parietal의 p-값이 0.045, Superior Parietal의 p-값이 0.041로 유의수준 내에서 유의 한 차이가 있는 것을 확인할 수 있었다(Supplementary Table 1).
다중공선성 확인
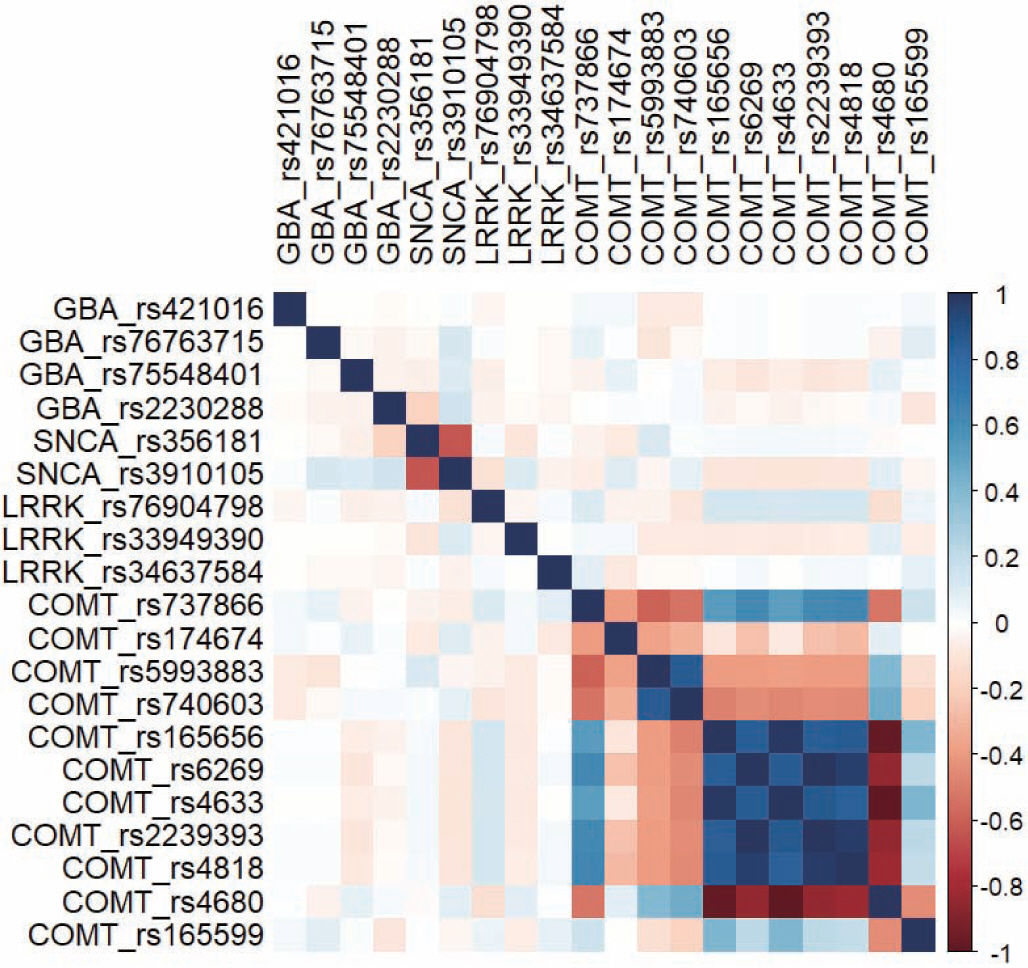
Figure 2는 SNP의 상관관계 행렬을 나타낸다. LRRK2와 GBA 유전 자에 속한 SNP들은 상관관계가 약한 반면 SCNA와 COMT 유전자에 속한 SNP들은 같은 유전자 종류의 SNP끼리 강한 상관관계를 가지고 있는 모습을 확인할 수 있었다. 따라서 이는 다중공선성이 존재할 가 능성을 확인하였고 다음으로 분산팽창지수를 확인한 결과 COMT 유 전자의 rs5993883, rs165656, rs6269, rs4633, rs2239393, rs4818, rs4680 변 수들의 분산팽창지수가 10이 넘는 것을 관찰할 수 있었다. 다음의 두 결과를 통해 같은 유전자의 SNP에서 다중공선성이 존재하는 것을 확 인할 수 있었다.
변수 선택
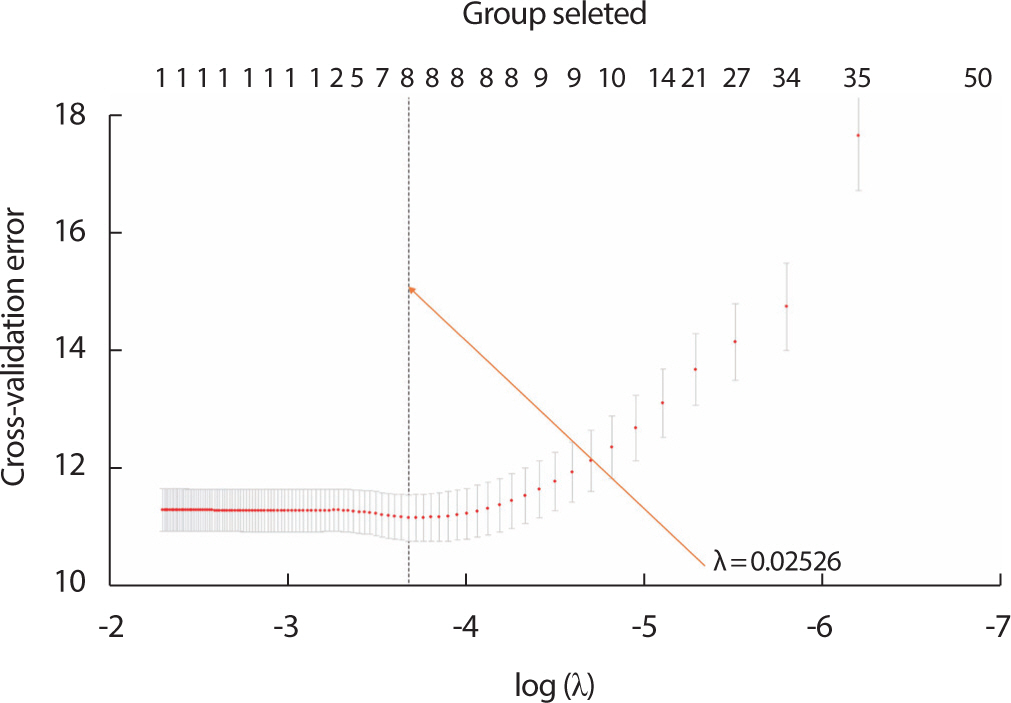
그룹 라쏘를 이용해 조율 모수인 를 조율하기 위해 5-fold cross validation 방법을 적용하였다. k-fold cross validation은 데이터셋을 k개의 데이터셋으로 나누어진 데이터들을 각각 한 번씩 검증데이터로 선택 해 선택하지 않은 나머지 데이터셋을 훈련용 데이터로 사용해 최적화 의 조율 모수를 구하는 방법이다. Figure 3은 값에 따른 cross validation 오류를 나타낸다. λ 의값이 0.02526일 때 cross validation 오류의 차이가 가장 작게 계산되었으며, 이때 선택된 커널 그룹의 개수는 총 7개이다. Figure 3에서 선택된 그룹의 개수가 8을 가리키고 있는 것을 확인할 수 있는데 이는 그룹에 포함하지 않은 인구통계학적 변수와 관 심 지역의 부피에 대한 변수를 한 개의 그룹으로 표시하기 때문에 이 것을 제외한 7개의 커널 변수 그룹이 선택되었다는 것을 의미한다. 추 정된 계수와 그룹 라쏘 페널티의 그룹에 대한 조정 변수는 Supplementary Table 2와 Supplementary Table 3에 각각 제시하였다.
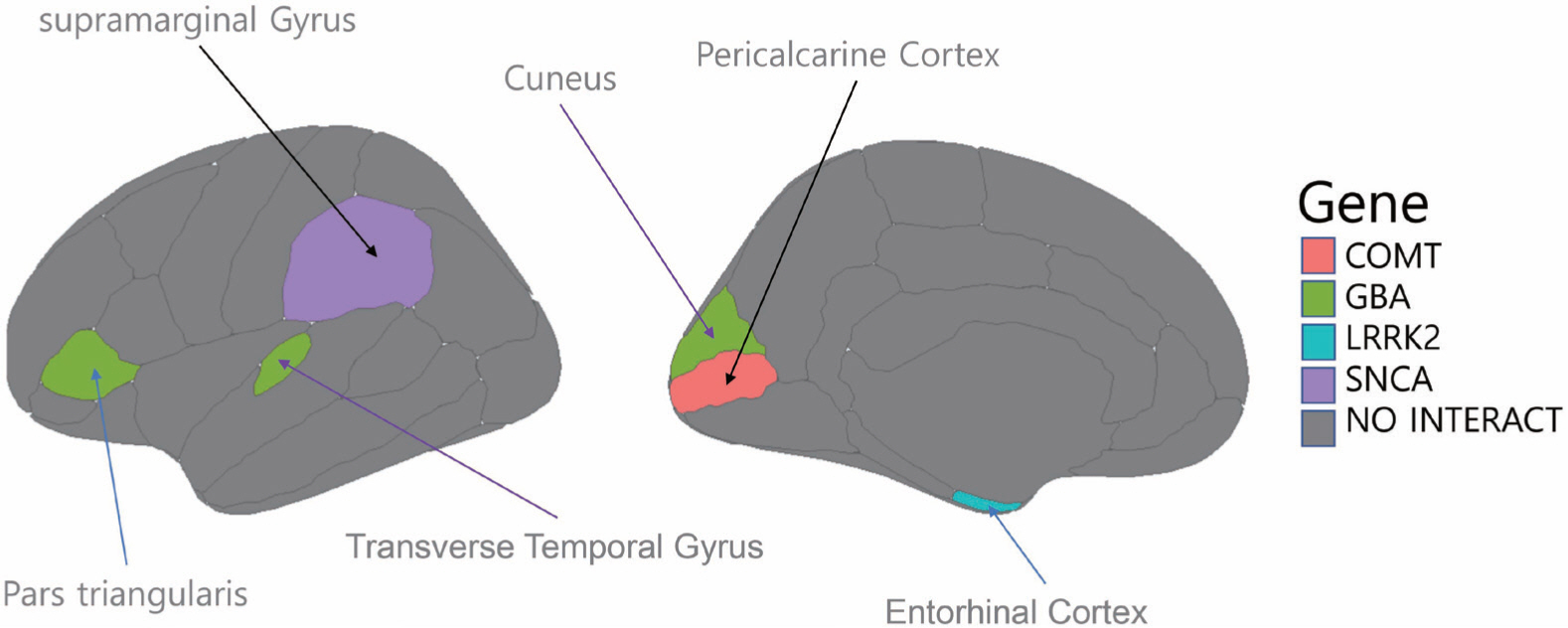
다음으로 어떠한 커널 변수가 선택되었는지 확인해 보면 유전자 커 널 중에서 LRRK2 커널이 선정되었고 교호작용 커널 여섯 가지가 선정 되었다. Figure 4는 왼쪽 그림은 좌뇌의 바깥면을 보여주는 그림이며 오른쪽 그림은 좌뇌의 안쪽 단면을 보여주는 그림으로, 선택된 교호작 용 커널을 바탕으로 교호작용이 있는 해당 관심 지역과 유전자를 표 현하였다. 교호작용 커널에서 선택된 관심 지역을 확인해 보면 총 여섯 가지 부위인 cuneus, pericalcarine cortex, transverse temporal gyrus, supramarginal gyrus, pars triangularis, entorhinal cortex이다. Cuneus와 pericalcarine cortex는 후두엽에 위치하며 시각 정보처리에 관여하는 부위이다. Transverse temporal gyrus는 청각 피질에 위치하며 청각 정 보처리에 관여하는 부위이며 supramarginal gyrus, pars triangularis는 각각 두정엽, 전두엽에 위치하며 언어정보처리에 관여하는 부위이다. Entorhinal cortex는 전두엽에 위치하며 기억형성 역할을 하는 지역이 다. 여섯 가지 부위의 공통점은 각각의 감각 정보 및 기억 정보를 처리 하는 부위라는 것이다. Pozzi et al. [14]의 연구에서 보행 동결과 관련 있는 관심 지역의 부위는 운동 기능과 관련된 부위인 precentral, superiorfrontal 등인데 직접적인 연관이 있는 부위가 아닌 다른 부위에서 결과가 나왔기 때문에 여섯 가지의 관심 지역에서 부피의 차이가 보행 동결 발생에 직접적인 영향을 주는 것이 아니라 다른 공통적인 곳에 서 영향을 받아 이러한 결과가 발생하였다고 해석할 수 있다.
고찰 및 결론
본 연구에서는 다중커널을 이용한 콕스 비례위험 모형을 통해 파킨 슨병 환자의 보행 동결 증상과 연관이 있는 유전적, 뇌영상학적 요인 을 밝히고자 하였다. 제안된 모델은 IBS 커널을 통해 같은 유전자에 속 하는 SNP 간의 상호관계를 고려하였으며, 뇌 부피와 유전자의 교호작 용 또한 포함할 수 있었다. 연구 결과, 감각 정보 및 기억 정보를 처리하 는 부위와 파킨슨병 발병 및 보행 동결과 관련된 유전자가 보행 동결 발생에 대한 교호작용이 있는 것을 확인할 수 있었다. 추가적으로, 커 널을 이용하지 않고 각 유전자 종류별 그룹 라쏘를 이용한 콕스 회귀 모형을 적합해 본 결과 어떠한 유전자도 선택되지 않았다. 즉, 본 연구 에서 고려한 커널 머신 모형을 활용한 콕스 모델을 통해 유전자 및 뇌 영상학적 요인과 보행 동결 발생의 비선형 관계성을 적절하게 분석할 수 있었다.
본 연구는 여러 한계가 존재한다. 기존 연구에서 밝혀진 관심 지역 부위와 다른 곳에서 교호작용이 존재한다는 결과가 나왔기 때문에 추 가로 여섯 가지 관심 지역의 부피와 유전자가 어떠한 메커니즘으로 교 호작용이 있는지, 그리고 기존에 밝혀진 부위와의 관계성에 대한 추후 연구가 필요하다. 또한 유전자와 교호작용이 있는 관심 지역의 부피가 보행 동결 발생에 어떠한 방향으로 영향을 주는지 추후 연구가 더 필 요할 것이다. 현재 적용한 데이터는 유전자와 관심 지역의 부피만을 활 용하였기에 다양한 요소를 추가로 고려하거나 더 고도화된 다중체 데 이터를 활용해 데이터를 구성하면 파킨슨병에서 보행 동결이 발생하 는 복합적인 과정을 더 명확히 설명할 수 있을 것이다. 또한, 최근까지 파킨슨병과 보행 동결에 관련된 유전자가 계속 발견되고 더 많은 유전 자를 추가로 반영한다면 지금의 결과보다 더 정확한 결과를 얻을 수 있을 것이다. 그리고 본 연구에서는 보행 동결과 관련된 유전자보다 파 킨슨병 발병에 관한 유전자가 더 많이 사용되었다. 추후 연구에서 보 행 동결과 관련된 유전자를 더 추가한다면 보행 동결과 직접적으로 연관이 있는 교호작용 커널을 찾을 수 있을 것으로 기대한다. 마지막 으로, 본 연구에서 제안한 모델은 주 효과인 유전자 효과와 교호작용 의 효과에 대한 계층적 구조를 고려하지 않은 모델이며 세부적인 신경 학적 메커니즘에 대한 이해가 더 필요하다는 한계가 있다. 추후 연구 에서 이를 보완하고 반영한다면 파킨슨병과 보행 동결의 발생에 정확 한 원인을 밝혀낼 수 있을 것이며 이를 활용해 비운동 증상 또한 발생 에 영향을 미치는 여러 요인을 찾을 수 있을 것으로 기대한다.
Supplementary Material
Supplementary Table 1.
Additional subject’s brain volume characteristics
Supplementary Table 2.
Estimated coefficients
Supplementary Table 3.
Group multipliers