R을 이용한 결과 변수에 따른 예측 모형과 시각화 - 회귀분석을 중심으로
Abstract
Predictive models have recently become increasingly important across various fields. In particular, in clinical research, the main purpose is to build a model that can find risk factors and predict a specific disease. Predictive models can help clinicians make fast and accurate decisions by capturing relationships between multiple factors related dependent variables. Accordingly, this paper describes a predictive model construction method and visualization that can be useful in clinical research. As dependent variables can be divided into continuous, categorical, and survival variables, the concepts and principles of linear, logistic, and cox regression analyses for building predictive models are explained in this paper. In addition, we investigated how to select variables to create an optimal model and how to evaluate the discrimination and calibration of the model. A visualization method that can help interpret according to each regression analysis model is also described. This paper will provide basic knowledge for clinical researchers to more easily build predictive models and evaluate them for practical use.
Key words: Predictive model, Regression, Visualization, Discrimination, Calibration
서 론
예측 모형은 공학, 수학, 의학 등 여러 분야에서 점점 중요한 부분을 차지하고 있다[ 1, 2]. 특히 임상연구에서 특정 질병에 영향을 주는 인자들을 찾고 그 질병을 예측할 수 있는 모형을 만드는 것은 주요한 관심사이다[ 3, 4]. 예측 모형은 여러 요인 간의 관계를 포착하여 유용한 정보를 추출해 정확한 임상연구 결과로 이어지게 한다[ 5]. 따라서, 임상연구에서 예측 모형의 구축은 제한된 시간 안에서 빠른 의사결정을 하게 하며, 보다 효율적으로 진단을 내릴 수 있게 하는 것을 목표로 가진다. 임상연구에서는 증상의 중증도 점수와 같은 연속형 자료나 질병 유무와 같은 범주형 자료, 또는 시간의 흐름에 따른 사망 혹은 질병 발생 여부를 결과 변수로 고려한다. 이때 예측을 위하여 적용할 수 있는 분석 방법은 선형, 로지스틱, 콕스(Cox) 회귀분석이 있다[ 6- 8]. 로지스틱과 콕스 회귀분석은 선형 회귀분석에서 일반화시킨 모형으로 직관적이고 활용도가 높아 최근 연구에서도 많이 사용되고 있는 분석이다. 회귀분석을 통해 예측 모형을 구축한 후, 시각화를 통해 예측 모형을 쉽게 이해하고, 모형의 정확도를 파악할 수 있다. 본 연구는 임상연구에서 예측 모형을 만들 때 사용할 수 있는 기본적인 방법을 설명함으로써 임상연구자가 본인이 원하는 예측 모형을 적절하게 세울 수 있게 하는 것을 목표로 한다. 2장에서는 종속변수의 유형에 따라 선형, 로지스틱, 콕스 회귀분석의 기본 개념을 소개하고, 3장에서는 모형에 사용할 변수를 선택하는 방법과 다중공선성 확인 방법에 대해서 알아보고자 한다. 4장에서는 회귀분석별 시각화 방법에 대해서 알아보고, 5장에서는 구축된 모형에 대하여 적합도와 성능을 평가할 수 있는 방법을 소개하고자 한다. 6장에서는 예측 모형을 다른 데이터에 적용하여 성능을 평가하는 방법을 설명하고, 7장에서는 예측 모형을 세울 때 주의할 점에 대해 소개하고자 한다. 또한, 모든 과정은 R을 통해 구현해 낼 수 있도록 R 코드를 제공하고자 한다.
예측 모형의 기본 개념
회귀분석은 인과관계를 검정하는 분석으로 하나 이상의 독립변수가 종속변수에 영향을 미칠 때 사용하는 방법이다[ 9, 10]. 일반적으로 회귀분석은 독립변수와 종속변수 간의 영향 관계를 설명하고, 회귀식을 통해 예측하는 것을 목적으로 한다. 이 장에서는 임상 연구에서 종속변수의 유형에 따라 예측 모형을 세울 수 있는 세 가지 회귀분석 방법을 소개하고자 한다. R 코드는 R에서 기본적으로 제공하는 데이터인 ‘ mtcars’와 ‘ survival’ 패키지에서 제공하는 ‘ colon’ 데이터를 사용하여 제시하였다. R code>data1<-mtcars; library (survival); data2<-colon
선형 회귀분석
선형 회귀분석은 연속형 종속변수에 영향을 미치는 인자를 찾을 때 이용하는 분석이다[ 11]. 독립변수가 여러 개인 다중 선형 회귀분석식은 (1)과 같으며, α와 β 값은 예측 값과 실제 값의 차이를 최소화시키는 값으로 추정하게 된다. 선형 회귀분석을 통해 얻은 식을 이용하여 독립 변수의 값을 알면, 종속 변수의 값을 예측할 수 있다. 예를 들어 y^=−223.72+39.06x1+34.9x2라는 선형 회귀 예측 식을 얻었고, x 1=10, x 2=15이면, y^=−223.72+39.06*10+34.9*15=46.17로 y 값을 예측 할 수 있다. 선형 회귀분석의 회귀계수 β i는 i번째 독립변수의 회귀계수로 1 증가 당 y^의 변화량을 의미한다 (2). Rcode> fit1<-lm(hp∼cyl+gear, data=data1); summary (fit1)
로지스틱 회귀분석
로지스틱 회귀분석은 질병 유무와 같은 범주형 종속변수에 영향을 미치는 인자를 찾을 때 사용하는 분석 방법이다[ 12]. 범주형 변수가 종속변수일 경우, 연속형 종속 변수를 대상으로 하는 선형 회귀분석에 적용이 불가능하다. 로지스틱 회귀분석은 선형 회귀분석(1)을 확장시킨 종속변수를 f(x)라는 함수로 치환한 일반화 선형모형의 한 형태이다[ 13]. 질병이 있을 확률을 p라고 할 때, 로지스틱 회귀분석에서는 질병이 있을 확률을 로짓변환한 형태를 이용하여 f(x)=lnp1−p라는 함수를 일반화 선형모형에 대입하여 적용한다 (3). 또한, 로지스틱 회귀분석에서는 개별 위험인자의 영향을 교차비(Odds ratio, OR)로 표현할 수 있으며, 이는 각 독립변수의 계수에 exponential을 취하여 구할 수 있다[ 14], (4). 만약 OR 값이 1보다 크면 요인에 의해 질병 위험이 증가하고, 1보다 작으면 감소함을 의미하며 로지스틱 회귀분석을 이용한 모형을 표현할 때는 보통 OR 값과 95% 신뢰구간 그리고 p-value로 결과를 제시할 수 있다. Rcode>fit2<-glm (status~sex+obstruct+perfor+adhere+surg,
콕스 회귀분석
콕스 회귀분석은 생존 유무와 생존 시간에 영향을 주는 인자를 찾을 때 사용하는 분석 방법이다[ 10]. 위험인자가 없을 때의 위험도와 위험인자가 있을 때의 위험도의 비례로써 모형을 구성하며, 이때 위험도의 비는 시간에 따라 일정하다고 가정한다. 이를 비례 위험 가정이라고 하며, 이를 전제로 한 비례 위험 가정 모형은 식 (5)와 같이 세울 수 있다. 이때, h( t)는 t시점에서의 사건 발생 위험도이며, h0(t)는 위험인자가 전혀 없을 때의 t시점에서의 사건 발생 위험도이다. 콕스 비례위험모형은 로지스틱 회귀분석과 마찬가지로 일반화 선형모형을 통해 회귀식 (6)을 유도할 수 있다. 비례위험 모형에서 독립변수의 계수에 exponential을 취하면 t시점에서 위험인자가 없는 경우에 비해 위험인자가 있을 때의 사건 발생의 위험도(hazards ratio, HR)이며 (7), 이 값이 1보다 크면 독립변수에 의해 사건 발생의 위험이 증가하고, 1보다 작으면 감소함을 의미한다. 콕스 회귀 모형을 이용한 분석 결과를 표현할 때는 보통 HR 값과 95% 신뢰구간, p-value로 결과를 제시할 수 있다.
Rcode>fit3<-coxph (Surv (time, status)~sex+obstruct+perfor+
예측 모형의 변수 선택법
예측 모형 구축 시 적절한 변수 선택은 중요하다. 보통 예측 모형에 많은 변수가 들어갈수록 그 모형의 설명력은 높아지지만, 무작정 많이 넣기만 할 경우 다중공선성의 문제, 과 적합의 문제로 오히려 실제로 적용하지 못하는 모형이 만들어질 수 있다.
회귀분석을 이용하여 모형을 만들고자 하는 경우, 임상연구에서는 일반적으로 ‘입력법’을 사용한다. 이는 고려하고자 하는 변수들을 단순 회귀분석을 통해 종속변수와의 관계를 파악하고, 유의하게 나타난 변수와 유의하지는 않았지만 임상적으로 중요하다고 판단되는 변수들을 다중 회귀분석에 넣어 모형을 만드는 방법을 의미한다. 그 외, 단순 회귀분석에서 유의한 변수가 많았고, 이를 모두 다중 회귀분석의 독립변수로 넣을 경우, 변수 간에 다중공선성의 문제가 생기는 경우가 있을 수 있다. 이럴 때는 변수 선택법을 이용하여 다수의 독립변수 중 일부를 선택해 줄 수 있다[ 15]. 변수 선택법 방법에는 절편만 있는 상수모형으로부터 시작해 중요한 설명변수부터 차례로 모형에 추가하는 ‘전진선택법’이 있으며, 모든 독립변수를 포함한 모형에서 출발해 가장 적은 영향을 주는 변수부터 하나씩 제거하면서 더 이상 제거할 변수가 없을 때까지 진행하는 ‘후진제거법’이 있다. 또한, 전진선택법에 의해 변수를 추가하면서 새롭게 추가된 변수에 기반하여, 기존 변수에 대한 중요도가 약화되면 해당 변수를 제거하며, 단계별로 추가 또는 제거되는 변수의 여부를 검토하여 더 이상 변경사항이 없을 때까지 진행하는 ‘단계선택법’이 있다. R에서는 Akaike Information Criterion (AIC) 또는 Bayesian Information Criterion (BIC)를 계산하고, 그 값이 최소가 되는 모형을 선택하는 방법을 제공하고 있으며, 시행할 수 있는 코드는 아래와 같다. 변수선택법의 코드는 전진선택법을 예로 들었으며, step 함수의 direction 조건을 “ backward” 또는 “ both”로 지정하면 후진제거법과 단계선택법을 적용할 수 있다.
Rcode>#입력법:
enter<-glm (status~sex+obstruct+perfor+adhere+surg, family=binomial, data=data2); summary (enter) #변수선택법: null<-glm (status~1, data=data2, family=”binomial”) full<-glm (status~sex+obstruct+perfor+adhere+surg, data=data2, family=“binomial”) forward<-step (null,scope=list (lower=null, upper=enter), direction=“ forward”, data=data2, family=”binomial”); summary (forward)
결정된 변수들이 최종적으로 적절한지 확인하기 위하여 다중공선성을 확인해야 한다. 다중공선성은 분산 팽창 인수(variance inflation factor, VIF) 수치를 이용하여 독립변수들 간의 상관성이 있는지 확인할 수 있으며, 보통 10보다 크면 그 독립변수는 다중공선성이 있다고 할 수 있다[ 16]. VIF가 10보다 큰 독립변수라면 해당 변수는 모형에서 제거하고 모형을 재구성하는 것을 고려해 볼 수 있다. Rcode>library (HH); vif (fit2)
시각화
예측 모형을 단순히 식으로만 나타내는 것 보다 시각화를 통해 표현하면 예측 모형이 잘 적합 되었는지 확인할 수 있으며 이해하기 쉽게 표현할 수 있다. 이 장에서는 각 회귀분석 모형에서 시각화 할 수 있는 방법과 그 해석 방법을 알아보고자 한다.
산점도와 회귀선 - 선형 회귀분석의 시각화
선형 회귀분석을 시각화하는 방법으로는 산점도와 회귀선을 그리는 방법이 있다[ 17]. 산점도는 선형 회귀분석을 하기 전, 실제로 독립변수와 종속변수가 선형의 관계를 가지고 있는지 시각적으로 확인할 수 있다. 예를 들어, 산점도를 그렸을 때, J자나 U자와 같이 선형적인 형태를 갖추고 있지 않다면, 독립변수와 종속변수가 선형의 관계를 갖는다고 보기는 어렵다. 이런 경우에는 선형 회귀분석이 아닌 다른 방법을 고안해야 한다. 반면, Figure 1A는 서로 직선의 관계를 가진다고 볼 수 있으며, 이러한 경우에는 선형 회귀분석을 통해 예측 모형을 구축할 수 있다. 또한, 예측 모형을 구성한 후에 회귀선과 산점도를 함께 그리면, 회귀 모형이 실제 값을 잘 예측하고 있는지 확인 가능하다. 하지만, 단순 선형 회귀분석에서는 독립변수가 1개로 산점도를 좌표평면에 그릴 수 있으나, 다중회귀분석은 여러 독립변수가 존재하기 때문에 한 평면에 산점도와 회귀선을 표현하는데 제약이 있다. 다중회귀분석에서 시각화를 하고자 한다면, 주요한 변수를 선택하여 단순 산점도와 회귀선으로 탐색적으로 표현하거나, Figure 1B와 같이 주요한 독립변수와 종속변수에 영향을 미치는 다른 변수들을 효과를 제거한 잔차를 이용하여 잔차 산점도와 회귀선으로 표현할 수 있다[ 18]. R code>plot (data$disp, data$hp); abline (fit0)
Figure 1
Visualization of the regression model. 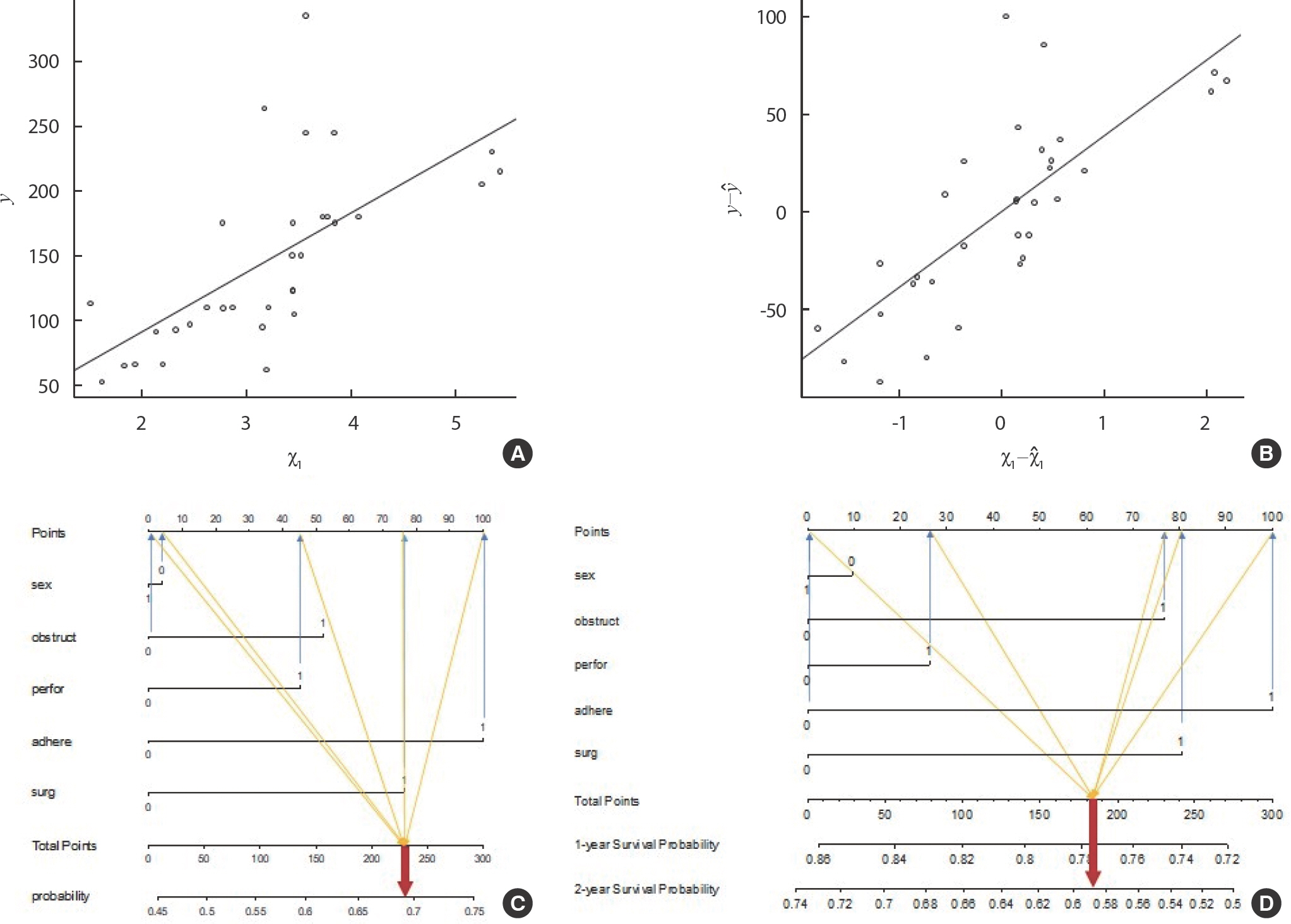
노모그램 - 로지스틱 회귀분석의 시각화
로지스틱 회귀분석을 시각화하는 방법으로는 노모그램(nomogram)을 그리는 방법이 있다. 노모그램은 예측 모형을 시각화하여 보여주고 쉽게 해석할 수 있도록 한 그래프이다[ 19, 20]. 특히 임상 연구에서는 질병의 위험 요인과 예측 확률을 쉽게 이해할 수 있도록 시각적으로 표현하는 통계적 도구로 활용되고 있다. 노모그램을 통해 결과에 각 예측 위험 요인의 효과가 어느 정도인지 시각적으로 파악할 수 있고, 각 환자의 다양한 위험 요인들에 해당하는 예측 확률을 쉽게 구할 수 있는 점이 특징이다. 노모그램을 구축하는 과정은 다음과 같으며, 기본적으로 점수는 가장 높은 영향을 미치는 변수에 대비한 나머지 변수들의 영향의 크기를 의미한다.
(1) 추정된 회귀계수 값의 절대값의 크기에 따라 순위를 매긴다. (2) 순위=1이면 점수 =100을 부여한다. (3) 순위=2인 경우 점수 =[(순위=2의 회귀계수 절대값)/(순위=1의 회귀계수 절대값)]∗100으로 점수를 설정한다. (4) 나머지 변수들에 대한 점수들도 3번과정을 반복하여 구한다. (5) 총 점수는 모든 변수의 점수를 더한 값으로 한다.
만약, 질병의 유무를 예측하기 위해 구축한 모형에 변수들의 회귀계수 값이 Table 1과 같고 모든 변수가 0과 1값을 가지는 이분형 변수일 경우, 노모그램은 다음과 같이 구성될 수 있다. (1) 각 변수의 회귀계수의 절대값 순서에 맞춰서 순위를 매긴다. (2) Rank가 1인 변수 ‘ Adhere’에 대한 점수는 100으로 설정한다. (3) 순위가 2인 변수 ‘ Surg’의 점수는 (0.35/0.46)∗100=76.36로 계산한다. 나머지 순위인 변수 ‘ Obstruct’, ‘ Perfor’, ‘ Sex’에 대해서도 (3)과 같이 계산함에 따라 총 점수는 277.81이 된다. 이렇게 계산된 값을 이용하여 노모그램을 그리면 Figure 1C와 같다. 이때 해석에 주의해야할 점은 sex의 경우 추정값이 -0.02로 음수이기 때문에 1일 때보다 0일 때 발생 확률이 높아짐을 의미한다. 노모그램을 통해 알 수 있듯이 sex는 1일 때 점수를 얻는 것이 아닌 0일 때 4점을 얻게 된다. 만약 변수 ‘ Adhere’, ‘ Surg’, ‘ Perfor’이 1이고, 변수 ‘ Obstruct’, ‘ Sex’가 0이라면, 점수는 100+76.36+0+45.28+4=225.64이고, 노모그램을 통해 질병이 있을 확률은 0.7보다 작고, 0.65보다 큰 것을 확인할 수 있다. 정확한 사건이 발생할 확률을 구하기 위한 식은 (8)와 같으며, 이에 대입하면 1/(1+exp(-(0.46+0.35+0.21-0.22))로 0.69로 노모그램 결과와 같음을 확인할 수 있다. 이처럼 모형을 구성하는 변수에 대한 값을 한 사람으로부터 얻을 수 있다면, 노모그램을 통해 그 사람이 질병에 걸릴 확률을 쉽게 파악할 수 있다. Yoon et al. [ 6]은 노모그램을 실제 임상 연구에 적용한 사례로 구축 방법 및 결과 해석 등을 참고할 수 있다.
Table 1
|
VariableS |
Estimates (beta) |
Absolute estimates |
Rank |
Points |
|
Adhere (1) |
0.46 |
0.46 |
1 |
100 |
|
Surg (1) |
0.35 |
0.35 |
2 |
76.36 |
|
Obstruct (1) |
0.24 |
0.24 |
3 |
52.17 |
|
Perfor (1) |
0.21 |
0.21 |
4 |
45.28 |
|
Sex (1) |
-0.02 |
0.02 |
5 |
4.00 |
|
intercept |
-0.22 |
|
|
|
|
Total points |
|
|
|
277.81 |
노모그램 - 콕스 회귀분석의 시각화
콕스 회귀분석도 로지스틱 회귀분석과 마찬가지로 노모그램을 통해 시각화가 가능하다[ 21, 22]. 다만, Figure 1D와 같이 콕스 회귀분석은 사건 발생 시간에 대한 개념이 들어 있어 노모그램에서는 1년, 2년 등 특정 시간 이후에 생존할 확률에 대한 예측을 시각화하여 표현할 수 있다. 콕스 회귀분석의 노모그램은 특정 시점에서 사건이 발생할 확률이 아닌 특정 시점에 생존할 확률에 중심을 두기 때문에 특정 시점에 생존할 확률은 식 (10)을 통해 구할 수 있다. 여기서 는 누적생존율로 각 시점마다 달라지는 값이며, Linear Predictor (LP)는 고정된 값이다 (9). 만약 변수 ‘ Sex’, ‘ Obstruct’, ‘ Perfor’, ‘ Surg’이 1이고, 변수 ‘ Adhere’가 0이라면, 점수는 0+77+26+0+80=183이며, 노모그램을 통해 1년 이후 생존할 확률은 0.78에 가깝고, 2년 이후 생존할 확률은 0.58과 0.6 사이임을 확인할 수 있다. 정확한 확률을 구하면 LP=-0.03∗ (1-0.52)+0.23∗(1-0.19)+0.08∗(1-0.08)+0.3∗(0-0.15)+0.24∗(1-0.27)= 0.38이고, S0(365)는 0.84로 1년 이후 생존할 확률은 [0.84] exp (0.38) =0.774이며, S0(730)은 0.7로 2년 이후 생존할 확률은 [0.7] exp (0.38) =0.594이므로 노모그램 결과와 같음을 확인할 수 있다.
예측 모형의 성능평가
앞서 소개한 회귀분석을 통해 구축된 예측 모형이 잘 적합 되었는지, 잘 예측을 할 수 있는지 확인하기 위해서는 적합도 확인과 성능평가를 수행해야 한다. 예측 모형의 성능을 평가하는 방법은 크게 Discrimination과 Calibration으로 나눌 수 있다. Discrimination은 모형이 실제 값을 잘 판별하는지 판별 능력을 확인하는 척도이며, Calibration 은 실제 값과 예측 값이 얼마나 일치하는지 일치 정도를 확인하는 방법이다.
결정계수와 5가지 평가지표 - 선형 회귀분석의 성능평가
선형 회귀분석에서 Discrimination을 평가하는 지표로는 결정계수(R square)가 있다[ 23], (11). 이는 회귀모형이 얼마나 의미가 있는지, 얼마나 선형에 가까운지를 확인할 수 있는 지표이다. 결정계수는 총변동 중에서 회귀모형에 의해 설명되는 비율을 나타낸다. 값은 0과 1사이로 표현되며, 1에 가까울수록 회귀식의 적합도가 높다고 해석할 수 있다. 하지만, 결정계수는 독립변수의 수가 많을수록 증가하기 때문에 이를 보정하기 위해 수정된 결정계수를 이용할 수 있다(12). 다른 지표로는 5가지 평가지표인 Mean Error (ME), Mean Absolute Error (MAE), Mean AbsolutePercentage Error (MAPE), Mean Square Error (MSE), Root Mean Square Error (RMSE)가 있다. ME는 단순히 오차 값의 평균을 의미하며(13), MAE는 ME의 절대값의 형태로(14), 오차의 크기를 그대로 반영하는 것이 특징이다. MAPE는 비율의 형태로 환산한 지표이며(15), MSE는 오차가 큰 부분에 더 높은 가중치를 주는 방법이다(16). 마지막으로, RMSE는 MSE에 루트를 씌운 지표이다[ 24], (17). 위 다섯 가지 지표는 값이 작을수록 성능이 좋음을 의미하며, 각 데이터의 특성에 따라 선택하여 성능을 평가할 수 있다. Calibration을 확인하는 방법으로는 잔차도를 통해 확인할 수 있다[ 25]. 잔차도는 Figure 2A와 같이 X축에 독립변수를 Y축은 잔차 (yi−y^)로 하여 그린 그림을 의미하며, 잔차도의 점들이 특정 형태를 띠지 않고, 일직선 0에 가깝게 고르게 분포되어 있을수록 예측 모형이 실제 값을 잘 예측한다고 볼 수 있다. Song et al. [ 8]를 통해 선형 회귀분석에서 모형의 성능을 판단할 수 있는 여러 지표에 대한 실제 적용 사례를 참고할 수 있다.
Figure 2
ROC curve and Calibration plot using logistic regression model. 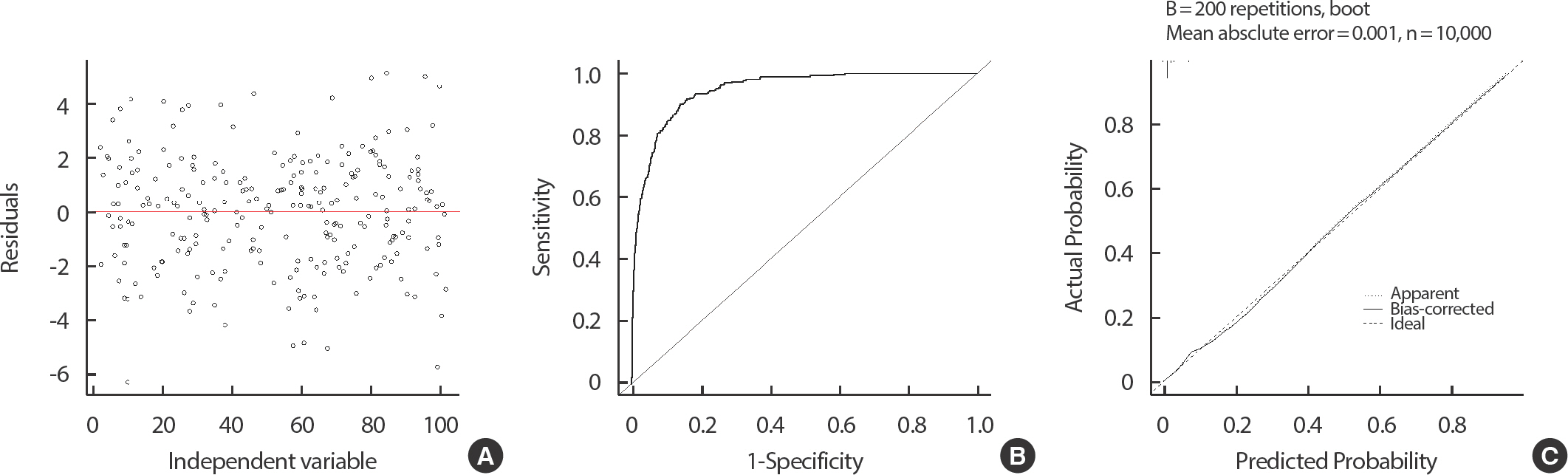
적합도 검정과 ROC 곡선 - 로지스틱 회귀분석의 성능평가
로지스틱 회귀분석에서 대표적으로 적합도를 평가하는 방법은 Hosmer-Lemeshow의 적합도 검정(Goodness-of-fit test)이 있다[ 26]. 예측 확률을 10분위수로 나누어 각 구간의 기대되는 사건의 수를 구하고, 각 구간의 실제 관측된 사건 수와 자유도가 8인 카이제곱 검정을 통해 비교할 수 있다. 이 검정의 귀무 가설 (H 0)은 “예측 모형은 적합하다”이며, 대립 가설 (H 1)은 “모형은 적합하지 않다”이다. 따라서, 검정의 p-value가 0.05보다 크면 예측 값과 실제 값이 유사하여 모형 적합이 잘 되었다고 판단할 수 있다. 로지스틱 회귀모형은 Receiver Operating Characteristic (ROC) 곡선 아래의 면적인 Area Under Curve (AUC)를 이용하여 Discrimination 을 평가하는 척도이다[ 27]. 여기서 ROC 곡선이란 민감도를 y축, 1-특이도를 x축으로 하여 그려지는 곡선을 의미한다. Figure 2B와 같이 y=x 선과 ROC 곡선 사이의 면적을 AUC라 하며, 이 값이 0.5에 가까우면 종속변수에 대한 변별력이 낮아짐을 의미하고, 1에 가까울수록 증가한다고 판단한다. Table 2를 참고하여, AUC에 따른 예측 모형의 성능 정도를 파악할 수 있다[ 28, 29].
Table 2
|
Area Under the Curve (AUC) |
Interpretation |
|
0.9≤AUC |
Excellent |
|
0.8≤AUC<0.9 |
Good |
|
0.7≤AUC<0.8 |
Fair |
|
0.6≤AUC<0.7 |
Poor |
|
0.5≤AUC<0.6 |
Fail |
로지스틱 회귀모형에서 Calibration은 Calibration plot을 통해 확인할 수 있다[ 30, 31]. 예측 확률과 실제 확률을 x축, y축으로 하여 45도 선에 가까우면 모형이 잘 만들어졌다고 판단한다[ 32]. Figure 2C에서는 Apparent, Biased-corrected에 해당하는 선이 모두 45도 선과 가까우므로 모형이 잘 적합 되었음을 확인할 수 있다.
C index와 ROC 곡선 - 콕스 회귀분석의 성능평가
콕스 회귀분석에서 모형의 적합도를 확인하는 방법에는 Harrell’s c index, Time dependent ROC curve, iAUC가 있다[ 33]. Harrell’s c index 는 Concordance Index라고도 불리며, 고전적인 방법으로 직관적인 해석이 가능하다. C index는 표본들을 생존 시간의 오름차순으로 나열하고, 사건이 관찰된 각 표본들보다 오래 생존한 표본들의 개수를 모두 더한 총합과 표본들을 예측된 생존 시간의 오름차순으로 나열하고, 사건이 관찰된 각 표본들보다 오래 생존할 것으로 올바르게 예측된 표본들의 개수를 모두 더한 총합의 비율로 계산된다. C index는 0과 1사이의 값을 가지며, 1에 가까울수록 정확하게 예측한다고 해석할 수 있으며, 0.5에 가까울수록 무작위로 예측한다고 해석한다[ 34]. R code>summary (fit3)
Time dependent ROC는 Kaplan Meier 생존함수 추정량과 베이즈 이론을 이용하여 모든 시점에서 sensitivity, specificity를 구하여 확인할 수 있다[ 35]. 기본적인 개념은 로지스틱 회귀분석의 ROC 곡선과 비슷하지만 시점별로 ROC 곡선의 모양이 다른 것이 특징이다. iAUC는 x 축을 시점, y축을 시점 t에서의 ROC curve의 아래 면적인 AUC 값을 이용한 통합 수치를 의미한다[ 36, 37]. 한편, 콕스 회귀분석의 calibration도 로지스틱과 마찬가지로 calibration plot을 이용하여 확인할 수 있다. 예측 확률과 실제 확률을 x축, y 축으로 하여 45도 선에 가까우면 모형이 잘 만들어졌다고 판단한다. Nahm et al. [ 7]을 통해 콕스 회귀분석을 이용한 예측 모형의 성능을 파악할 수 있는 실제 사례를 참고할 수 있다. Table 3은 이전까지 내용을 정리한 표이다.
Table 3
Characteristic of regression model
|
Outcome |
Continuous |
Categorical |
Survival |
|
Predictive model |
Linear |
Logistic |
Cox |
|
Model formula |
y^=α+β1x1+β2x2+⋯
|
lnp1−p=α+β1x1+β2x2+⋯
|
lnh(t)h0(t)=β1x1+β2x2+⋯
|
|
Interpretation |
Linear change |
Odds ratio (OR) |
Hazard ratio (HR) |
|
Variable selection |
|
Enter, Forward, Backward, Stepwise |
|
|
Visualization |
Scatter plot |
Nomogram |
Nomogram |
|
Discrimination |
R-square |
ROC curve, AUC |
Harrell's c index, Time dependent ROC curve, Integrated AUC |
|
Calibration |
Residual plot |
Calibration plot |
Calibration plot |
예측 모형의 외적 타당도 평가
구축한 예측 모형을 실제로 사용하기 위해서는 모형을 구축한 자료 이외에 새로운 자료에서도 예측을 잘할 수 있는지 확인하는 과정이 필요하다[ 38]. 새로운 자료에 예측 모형을 적용하여 Discrimination과 Calibration을 확인하여 평가 가능하다. 만약 로지스틱 회귀분석을 통해 예측 모형을 구축하였다면, 새로운 자료에 모형을 적합시킨 후, Calibration plot이 여전히 45도 선에 가까운지, ROC curve를 그렸을 때 AUC가 0.7 이상인지를 확인하여 성능을 평가할 수 있다.
예측 모형 구축 시 주의사항
예측 모형을 구축할 때에는 몇 가지 주의 사항이 있다. 첫째로 모형에 충분한 변수를 고려해야 한다는 점이다. 모형에 포함할 변수를 결정할 때 가능한 종속 변수에 영향을 줄 수 있는 모든 변수들을 고려하는 것이 좋다. 다양한 변수들의 조합을 고려한 모형은 더 안정적일 수 있으며, 높은 예측력을 기대할 수 있다. 보통 선형 회귀분석에서는 총 자료 개수의 1/10 정도, 로지스틱과 콕스 회귀분석은 총 사건의 수의 1/10 정도가 예측 모형에 들어갈 수 있는 적절한 독립변수 개수이다[ 39, 40]. 예를 들어 로지스틱 회귀분석에서 200개의 표본 중 60개가 사건 수에 해당한다면 6개 정도의 독립 변수가 모형에 포함되는 것이 적합하다고 볼 수 있다. 하지만 이는 꼭 지켜야하는 원칙은 아니며, 연구자가 상황에 따라 적절히 판단하는 것이 좋다[ 41]. 판단의 근거로는 독립 변수의 다중공선성 확인, 모형의 성능 평가가 될 수 있다. 둘째로 모형을 만들기 위해서는 모형을 만들 때 사용하는 자료와 모형의 외적 타당도 평가를 위한 자료의 표본 수의 비율은 7:3 정도가 적절하다고 알려져 있다[ 42]. 하지만 이는 확보할 수 있는 자료의 개수가 적을 때 최소한으로 지켜야하는 비율을 말하며, 상황에 따라 조정이 가능하다.
고 찰
본 연구는 임상 연구에서 종속변수가 연속형, 범주형 또는 생존 변수일 때 예측 모형을 구축하는 방법을 알아보았다. 선형, 로지스틱, 콕스 회귀분석을 사용하여 예측 모형을 구축할 수 있으며, 이때, 적절한 변수를 선택하는 방법에는 전진 선택법, 후진 제거법, 단계 선택법이 있었다. 예측 모형을 산점도, 노모그램 등을 이용하여 시각화하여 모형을 쉽게 이해하고 평가할 수 있는 방법을 알아보았다. 모형 구축 후에는 항상 성능 평가가 따라야 하며, 선형 회귀분석에서는 결정계수, 잔차도를, 로지스틱과 콕스 회귀분석에서는 ROC 곡선의 AUC와 Calibration plot를 통해 모형의 성능을 평가할 수 있었다. 최종 예측 모형을 실제 상황에서 적용하기 위해서는 새로운 자료에 대해서 검증이 필수적이며, 새로운 자료에 구축된 예측 모형을 적용하여 회귀분석 방법에 따라 Discrimination과 calibration을 확인하여 최종 예측 모형을 결정할 수 있다.
예측 모형 구축 및 시각화와 성능 평가 방법은 본 논문에서 다룬 것 이외에도 여러 방법이 존재한다. 최근에는 랜덤 포레스트 모형, 서포트 벡터머신, 신경망 모형 등 다양한 머신 러닝 기법도 개발되어 이를 활용하여 더 정교하게 예측 모형을 구축할 수도 있다[ 43- 47]. 또한 Net Reclassification Index (NRI), Integrated Discrimination Index (IDI) 등 다양한 성능 평가 방법이 존재하여 종합적으로 모형의 성능을 평가해 볼 수 있다[ 48]. 본 연구에서는 직관적이고 가장 많이 활용하는 방법에 대해 설명하였으며, 이를 통해 조금 더 임상 연구자들이 확장해 나가길 바란다. 지금까지 종속변수의 형태에 따라 예측 모형을 구축할 수 있는 몇 가지 방법을 살펴보았다. 모형을 구축할 때에는 구축 과정을 잘 따라가면서, 가장 효율적으로 예측할 수 있는 모형을 구성해야 한다. 모형에 너무 많은 변수를 넣어서도, 너무 적은 변수를 넣어서도 안 되며 변수 간에 다중 공선성 문제가 있어서는 안 된다. 또한, 구축된 모형은 항상 평가가 이루어져야 하며, 실제로 적용하기 위해 어느 데이터에서나 일정 수준 이상의 예측력을 보여야 한다. 본 논문을 통해 임상 연구자들은 예측 모형을 적절하게 구축하고, 이를 통해 올바르고 빠른 의사결정을 할 수 있기를 바란다.
REFERENCES
4. Greiner M, Pfeiffer D, Smith R. Principles and practical application of the receiver-operating characteristic analysis for diagnostic tests. Pre Vet Med 2000;45(1-2):23-41. DOI: 10.1016/s0167-5877(00)00115-x.  5. Friedman LM, Furberg CD, DeMets DL, Reboussin DM, Granger CB. Fundamentals of clinical trials. 5th ed.. Cham: Springer; 2015.
6. Yoon JH, Lee HS, Kim EK, Moon HJ, Kwak JY. A nomogram for pre-dicting malignancy in thyroid nodules diagnosed as atypia of undetermined significance/follicular lesions of undetermined significance on fine needle aspiration. Surgery 2014;155(6):1006-1013. DOI: 10.1016/ j.surg.2013.12.035.   9. Draper NR, Smith H. Applied regression analysis. 326: Hoboken: John Wiley & Sons; 1998.
10. Harrell FE. Regression modeling strategies: with applications to linear models, logistic regression, and survival analysis. 608: New York: Springer; 2001.
11. Seber GA, Lee AJ. Linear regression analysis. 329: Hoboken: John Wiley & Sons; 2012.
12. Kleinbaum DG, Dietz K, Gail M, Klein M, Klein M. Logistic regression. New York: Springer-Verlag; 2002. p. 536.
13. Faraway JJ. Extending the linear model with R: generalized linear, mixed effects and nonparametric regression models. Boca Raton: Chapman and Hall/CRC; 2016.
15. Mehmood T, Liland KH, Snipen L, Sæb⊘ S. A review of variable selection methods in partial least squares regression. Chemom Intell Lab Syst 2012;118:62-69. DOI: 10.1016/j.chemolab.2012.07.010.  16. Daoud JI. Multicollinearity and regression analysis. J Phys: Conf Ser 2017;949:012009.   17. Ryan TP. Modern regression methods. 655: New York: John Wiley & Sons; 2018.
18. Field A, Miles J, Field Z. Discovering statistics using R. London: Sage publications; 2012.
19. Zlotnik A, Abraira V. A general-purpose nomogram generator for predictive logistic regression models. Stata J 2015;15(2):537-546.   20. Iasonos A, Schrag D, Raj GV, Panageas KS. How to build and interpret a nomogram for cancer prognosis. J Clin Oncol 2008;26(8):1364-1370. DOI: 10.1200/JCO.2007.12.9791.   21. Kattan MW. Comparison of Cox regression with other methods for determining prediction models and nomograms. J Urol 2003;170(6 Pt 2):S6-S10. DOI: 10.1097/01.ju.0000094764.56269.2d.   23. Myers RH, Myers RH. Classical and modern regression with applications. 2: Belmont: Duxbury press; 1990. p. 488.
25. Zeileis A, Hothorn T. Diagnostic checking in regression relationships. R News 2002;2(3)):7-10..
26. Fagerland MW, Hosmer DW. A generalized Hosmer–Lemeshow good-ness-of-fit test for multinomial logistic regression models. Stata J 2012;12(3):447-453.   28. Carter JV, Pan J, Rai SN, Galandiuk S. ROCing along: Evaluation and interpretation of receiver operating characteristic curves. Surgery 2016;159(6):1638-1645. DOI: 10.1016/j.surg.2015.12.029.   29. Cook NR. Use and misuse of the receiver operating characteristic curve in risk prediction. Circulation 2007;115(7):928-935. DOI: 10.1161/ CIRCULATIONAHA.106.672402.   30. Meurer WJ, Tolles J. Logistic regression diagnostics: understanding how well a model predicts outcomes. JAMA 2017;317(10):1068-1069. DOI: 10.1001/jama.2016.20441.   31. Zemek R, Barrowman N, Freedman SB, Gravel J, Gagnon I, McGahern C, et al. Clinical risk score for persistent postconcussion symptoms among children with acute concussion in the ED. JAMA 2016;315(10)):1014-1025.. DOI: 10.1001/jama.2016.1203.   32. Steyerberg EW, Vickers AJ, Cook NR, Gerds T, Gonen M, Obuchowski N, et al. Assessing the performance of prediction models: a framework for some traditional and novel measures. Epidemiology 2010;21(1)):128-138.. DOI: 10.1097/EDE.0b013e3181c30fb2.   33. D’ Agostino RB, Nam BH. Evaluation of the performance of survival analysis models: discrimination and calibration measures. Handbook Stat 2003;23:1-25. DOI: 10.1016/S0169-7161(03)23001-7.
34. Steck H, Krishnapuram B, Dehing-Oberije C, Lambin P, Raykar VC. On ranking in survival analysis: bounds on the concordance index. Advances in neural information processing systems 20:2007.
36. Guinney J, Wang T, Laajala TD, Winner KK, Bare JC, Neto EC, et al. Prediction of overall survival for patients with metastatic castration-resistant prostate cancer: development of a prognostic model through a crowdsourced challenge with open clinical trial data. Lancet Oncol 2017;18(1):132-142. DOI: 10.1016/S1470-2045(16)30560-5.  37. Heagerty PJ, Zheng Y. Survival model predictive accuracy and ROC curves. Biometrics 2005;61(1):92-105. DOI: 10.1111/j.0006-341X.2005. 030814.x.   38. König IR, Malley JD, Weimar C, Diener HC, Ziegler A. Practical ex-periences on the necessity of external validation. Stat Med 2007;26(30)):5499-5511.. DOI: 10.1002/sim.3069.   39. Peduzzi P, Concato J, Feinstein AR, Holford TR. Importance of events per independent variable in proportional hazards regression analysis II. Accuracy and precision of regression estimates. J Clin Epidemiol 1995;48(12):1503-1510. DOI: 10.1016/0895-4356(95)00048-8.   40. Peduzzi P, Concato J, Kemper E, Holford TR, Feinstein AR. A simulation study of the number of events per variable in logistic regression analysis. J Clin Epidemiol 1996;49(12):1373-1379. DOI: 10.1016/ s0895-4356(96)00236-3.   41. Vittinghoff E, McCulloch CE. Relaxing the rule of ten events per variable in logistic and Cox regression. Am J Epidemiol 2007;165(6):710-718. DOI: 10.1093/aje/kwk052.   43. Mitchell TM. Machine learning. New York: McGraw-hill; 1997.
44. Mitchell TM. Machine learning and data mining. Commun ACM 1999;42(11):30-36. DOI: 10.1145/319382.319388.  45. Iavindrasana J, Cohen G, Depeursinge A, Müller H, Meyer R, Geiss-buhler A. Clinical data mining: a review. Yearb Med Inform 2009;18(01)):121-133.  46. Rodriguez-Galiano V, Sanchez-Castillo M, Chica-Olmo M, Chica-Ri-vas MJOGR. Machine learning predictive models for mineral prospec-tivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol Rev 2015;71:804-818. DOI: 10.1016/j.oregeorev.2015.01.001.  47. Smith AE, Mason AK. Cost estimation predictive modeling: Regression versus neural network. Engineering Economist 1997;42(2):137-161.  48. Pencina MJ, D'Agostino RB Sr, D'Agostino RB Jr, Vasan RS. Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond. Stat Med 2008;27(2):157-172. DOI: 10.1002/sim.2929.  
|
|













