서 론
최근 유방암(breast cancer)의 발병률이 높아지면서 유방암에 의한 사망률을 줄이기 위한 조기 발견 및 정확한 진단은 무엇보다 중요하다. 2017년 12월 보건복지부가 발표한 중앙암등록본부의 통계에 따르면 2015년 우리나라에서 새로 발생한 암환자 수는 214,701명으로 그 중 유방암은 19,219명으로 전체 암의 9.0%로 다섯 번째로 많이 발생한 암이고 여성에게 발생한 암 중에서는 갑상샘암에 이어 두 번째의 발생빈도를 보이고 있으며 1999년 이후 지속적인 증가추세를 보이고 있다[1].
유방암을 진단하는 데 기본적인 방법으로 유방촬영술(mammography), 유방초음파(ultrasonography), 세침 검사(fine needle aspiration, FNA) 등이 있다[2,3]. 유방촬영술은 가장 대표적이고 기본적인 유방검사법이고 유방초음파 검사는 고해상도 초음파 기기를 이용하여 유방 질환을 진단하는 검사로 주로 유방촬영술에서 치밀 유방을 보이는 여성에게 사용되는 검사이다. 세침 검사는 가는 주사바늘을 종양이 있는 부위에 찔러 세포를 채취하여 암인지 여부를 검사하는 방법으로 수술하지 않고 검사하기 때문에 간편하나 충분한 양의 조직을 얻기 힘들기 때문에 정밀한 진단을 내리는 데 한계를 갖고 있다.
최근 빠른 컴퓨터 기술 발달로 인하여 머신러닝(machine learning)이 암 진단에 활용되고 있다. 여기서 머신러닝이란 컴퓨터를 인간처럼 학습시켜, 스스로 규칙을 생성하도록 하는 기술을 말하는데 대표적인 방법으로는 k-근접 이웃(k-nearest neighbor), 의사결정나무(decision tree), 신경망(neural network), 서포트 벡터 머신(support vector machine), 판별분석(discriminant analysis), 로지스틱회귀분석(logistic regression analysis) 등이 있다[4-8]. k-근접 이웃 방법은 가장 유사한 상위 k개의 데이터로부터 다수결의 원칙(majority voting)에 의해 새로운 데이터의 분류를 결정하는 방법으로 높은 정확도를 갖는 반면에 계산비용이 높다는 단점을 갖고 있다. 의사결정나무는 분류함수를 의사결정 규칙으로 이루어진 나무모양으로 그려서 분류하는 방법으로 이해하기 쉬운 장점을 갖고 있으나 가지분할을 위한 변수 선택에 따라 결과가 달라지는 어려움이 있다. 그리고 신경망은 사람의 두뇌가 의사 결정하는 형태를 모방하여 분류하는 방법으로 과대적합(over-fitting)과 국소최적화(local optimization) 등의 한계점을 갖고 있다. 그리고 서포트 벡터 머신은 학습과정에서 마진(margin)을 최대화하는 초평면(hyperplane)을 추정한 후 새로운 데이터를 분류하는 방법으로 신경망에서 비해 과대적합이 덜하고 예측의 정확도가 높으나 결과에 대한 설명력이 떨어진다는 단점이 있다. 판별분석은 판별함수를 이용하여 개체들이 소속 그룹을 결정하는 방법으로 독립변수들이 다변량 정규분포(multivariate normal distribution)를 따른다는 가정하에서 효과적이고, 로지스틱 회귀분석은 종속변수가 범주형인 경우 사용하는 회귀분석의 확장방법으로 엄격한 가정을 요구하는 판별분석에 대한 대안으로 많이 사용한다. 위에서 살펴본 바와 같이 모든 경우에 우수한 성능을 갖고 있는 만능의 머신러닝 기술은 존재하지 않으며 제각기 장단점을 갖고 있다.
최근 들어 많이 이용되고 있는 딥러닝(deep learning)은 머신러닝 기술의 한 분야로, 인공신경망(artificial neural network)에 기반을 둔 심층신경망(deep neural network)으로 다양한 분야에서 뛰어난 성능을 보이고 있다[9].
본 연구에서는 유방암 분류성능 향상을 위해 딥러닝기반 앙상블(deep learning- based ensemble) 모형을 구축하고 기존의 단일 모형들과의 성능을 비교하고자 한다. 앙상블 방법으로 배깅(bagging), 부스팅(boosting), 스태킹(stacking) 등이 있다. 배깅은 주어진 학습자료에서 붓스트랩 표본(bootstrapped sample)을 생성하여 단일모형 결과들의 통합 전략(aggregation strategy)에 의해 분류하는 방법이고, 부스팅은 잘 분류되지 않는 약한 분류모형들을 결합하여 강한 예측모형을 만드는 방법이다. 스태킹은 배깅, 부스팅보다는 덜 알려졌지만 형태가 다른 여러 모형(heterogeneous models)을 결합함으로서 보다 안정적인 결과값을 도출할 수 있는 모형이다[10,11].
본 연구에서 제안한 딥러닝기반 앙상블 모형은 두 단계에 걸쳐 이루어진다. 첫 번째 단계에서는 스태킹 앙상블 방법을 수행한 후 두 번째 단계에서는 딥러닝을 적용하여 최종 분류한다.
모형의 성능 평가는 University of California at Irvine (UCI)의 머신러닝 데이터베이스(UCI Machine Learning Repository) [12]에서 제공되는 유방암 자료를 가지고 평가하고자 한다.
연구 자료
본 연구에서 분류모형의 성능평가에 사용한 자료는 UCI의 유방암에 대한 Wisconsin Original Breast Cancer (WOBC) 자료와 Wisconsin Diagnostic Breast Cancer (WDBC) 자료이다.
WOBC 자료
WOBC 자료는 1992년 UCI Machine Learing Repository [12]에 의해 제공되었고 많은 연구자에 의해 패턴 인식과 기계학습에 사용되고 있다. WOBC 자료는 699명에 대해 조사되었고 Table 1과 같이 클래스를 나타내는 변수와 FNA의 세포 특성을 나타내는 9개의 변수로 구성되어 있다.
여기서 세포 특성값은 1부터 10까지 스케일된 값을 가지고 1에 가까울수록 양성을 나타내고 10에 가까울수록 악성을 나타낸다.
WDBC 자료
WDBC 자료는 1995년 UCI Machine Learing Repository [12]에 의해 제공되었고 WOBC 자료와 함께 패턴 인식과 기계학습에 널리 사용되고 있는 자료이다. WDBC 자료는 569명에 대해 조사하였고 Table 2와 같이 양성과 악성을 나타내는 클래스 변수, 즉 Diagnosis 변수 1개와 세포 특성을 나타내는 10개의 변수, 즉 radius, texture, perimeter, area, smoothness, compactness, concavity, concave points, symmetry, fractal dimension에 대해 각각 평균과 표준편차 그리고 이상값(혹은 최대값)을 조사한 총 30개의 변수로 구성되어 있다.
예를 들면, radius 변수에 대해 3개의 변수 즉, 평균을 나타내는 mean radius 변수, 표준편차를 나타내는 radius SD 변수, 그리고 이상값을 나타내는 worst radius 변수가 존재한다.
연구 방법
기존의 분류 모형
k-근접 이웃
k-근접 이웃 모형은 분류하고자 하는 새로운 데이터에 대해 그 데이터와 가장 유사한 k개의 데이터 집합을 찾아서 그 집합의 데이터들이 속하는 다수결의 집단으로 분류하는 방법이다. 이때 k 값의 선택은 분류 결과에 많은 영향을 준다. k 값이 너무 작으면 근접 이웃 분류 모형은 훈련용 데이터의 잡음 때문에 과대적합될 가능성이 있고 반대로 k값이 너무 크면 분류하고자 하는 데이터에 가까운 집단으로 분류되지 않을 가능성이 있다.
의사결정나무
의사결정나무는 여러 가지 규칙을 순차적으로 적용하면서 독립 변수 공간을 분할하는 분류 모형으로 단계별로 설명하면 다음과 같다[13].
단계 1: 여러 가지 독립 변수 중 하나의 독립 변수를 선택하고 그 독립 변수에 대한 기준값을 정한다. 이를 분류 규칙이라고 한다.
단계 2: 전체 학습 데이터 집합(부모 노드)을 해당 독립 변수의 값이 기준값보다 작은 데이터 그룹(자식 노드 1)과 해당 독립 변수의 값이 기준값보다 큰 데이터 그룹(자식 노드 2)으로 나눈다.
단계 3: 각각의 자식 노드에 대해 위의 단계 1과 단계 2를 반복하여 하위의 자식 노드를 만든다. 단, 자식 노드에 한 가지 클래스의 데이터만 존재한다면 더 이상 자식 노드를 나누지 않고 중지한다.
서포트 벡터 머신
다음의 학습자료 (learning dataset) D가 주어졌다고 가정하자
여기서 yi는 p차원 벡터 χi가 속하는 클래스를 나타내는 값으로 +1 혹은 -1이다. 서포트 벡터 머신에서 χi를 두 클래스로 분류하기 위한 최적 분리 초평면 (optimal separating hyperplane)은 각 클래스에 속하는 점들 중에서 서포트 벡터를 지나는 두 개의 평행인 초평면들 사이의 거리, 즉 마진을 최대로 함으로써 결정된다. 우리는 슬랙변수(slack variable) ξi(≥0)을 도입하여 다음과 같이 최적화 문제를 형식화할 수 있다.
여기서 C는 마진의 최대화와 분류 오류율의 최소화 사이 트레이드-오프(trade-off)를 결정하는 모수이다. 커널 함수(kernel function)K(χi,χj)을 도입하여 식(3.1)의 최적화 문제를 다음과 같이 나타낼 수 있다.
여기서 αi는 라그랑지 배수(Lagrange multiplier)이다. 따라서 서포트 벡터를 사용하여 최적의 분리 평면을 다음과 같이 입력벡터 χ의 결정함수를 나타낸다.
여기서 S는 서포트 벡터를 나타내고 b는 원점으로부터 거리(offset)이다.
판별분석
판별분석은 최초 Fisher [14]에 의하여 체계화된 통계이론으로서 전체 집단을 두 개 이상의 집단으로 분류함에 있어 분류오차를 최소화할 수 있는 판별규칙을 도출하여 새로운 개체를 소속 집단으로 분류하는 방법으로 독립변수들은 다변량 정규분포를 이루고, 또한 각 집단의 공분산 행렬이 동일하다는 가정하에 성립된다.
딥러닝 기반 앙상블 모형
딥러닝
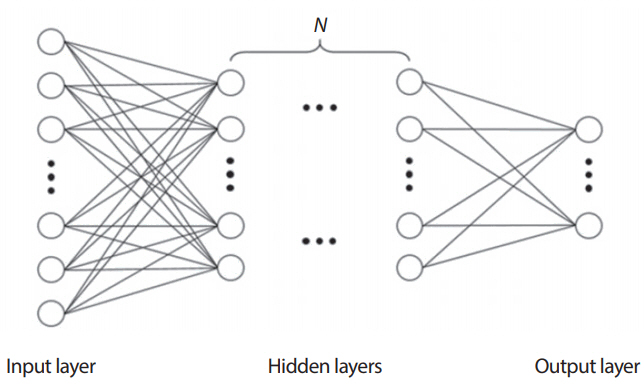
Figure 1은 입력층(input layer)과 출력층(output layer) 사이에 여러 개의 은닉층(hidden layer)을 갖고 있는 심층 신경망의 예를 보여주고 있다. 심층신경망은 많은 은닉층의 개수를 늘림으로써 여러 비선형 변환기법의 조합을 통해 높은 수준의 추상화(abstractions)가 가능한 신경망 구조이다.
Figure 1에서 층의 수가 nl개이고 층 l를 Ll이라 표현하자. 그러면 Ll은 입력층, Lnl은 출력층, 그리고 L2, …, Lnl-1은 은닉층을 나타낸다. 그리고 신경망에서 학습할 모수는 다음과 같다.
여기서
이때 W i j l b i l
심층신경망을 통해 학습할 m개의 훈련 데이터는 다음과 같다.
우리는 확률적 경사 하강법(stochastic gradient descent)을 통하여 심층신경망을 학습하고자 한다. 이를 위해 비용함수(cost function)를 다음과 같이 정의한다.
(3.2)
여기서 첫 번째 항은 평균 제곱 오차 항(mean square error term)이고 두 번째 항은 정규화 항(regularization term)은 나타내고 λ
식(3.2)의 비용함수를 최소화하는 파라미터는 다음과 같이 반복적인 방법에 의해 구한다.
여기서 α는 학습률을 나타낸다.
스태킹 앙상블 모형
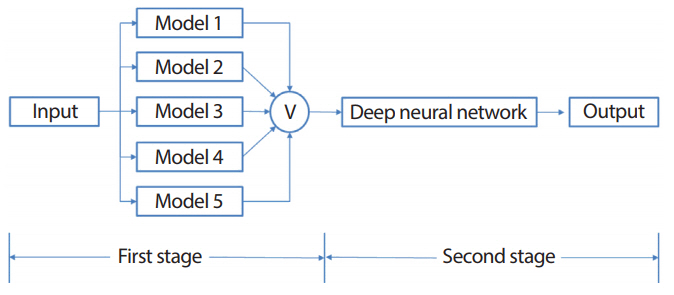
제안된 딥러닝기반 앙상블 모형은 Figure 2에서 보는 것처럼 크게 두 단계에 걸쳐 이루어진다. 첫 번째 단계에서는 입력 데이터에 스태킹 앙상블 방법을 수행한 후 두 번째 단계에서는 딥러닝을 적용하여 최종 분류한다.
5-조각 교차 타당성하에서 Figure 2의 딥러닝기반 앙상블 모형을 단계별로 설명하면 다음과 같다.
[First Stage]
단계 1. 주어진 자료 D를 조각 크기가 같도록 5-조각 D1, D2, …, D5으로 분할한다. 여기서 Dk={xk,yk, k=1,...,5}
단계 2. 분할된 5-조각 중에서 4조각의 합집합 즉, ∪ k = 2 5 D k
단계 3. 훈련용 자료 ∪ k = 2 5 D k
단계 4. 단계 3에서 얻은 모형의 예측확률 H1과 주어진 라벨(목표변수)y1을 합병(merge)하여 새로운 자료 D 1 ' = H 1 , y 1
단계 5. 5-조각 교차 타당성에 의해 훈련용 자료와 테스트용 자료에 대해 역할을 교환하면서 위의 단계를 5번 반복 수행하여 새로운 데이터 셋 D 1 ' , D 2 ' , … , D 5 ' D k ' = H k , y k , k = 1 , … , 5
[Second Stage]
단계 6. 단계 5에서 얻어진 새로운 데이터 셋 D 1 ' , D 2 ' , … , D 5 ' D 2 ' , … , D 5 ' ∪ k = 2 5 D k ' D 1 ' = H 1 , y 1
단계 7. 훈련용 자료 ∪ k = 2 5 D k ' D 1 ' = H 1 , y 1
단계 8. 5-조각 교차 타당성에 의해 위의 단계를 5번 반복 수행하여 최종 분류한다.
본 연구에서 사용된 기본 분류모형으로는 k-근접 이웃, 의사결정나무, 서포트 벡터 머신, 판별분석, 로지스틱 회귀분석을 고려한다.
성능평가 측도
본 연구에서 제안한 딥러닝기반 앙상블 모형의 성능 평가를 위해 성능 평가 측도인 정확도(accuracy), Receiver Operating Characteristics (ROC) 곡선과 c-통계량(c-statistics) 등을 가지고 비교하고자 한다. 제안한 딥러닝기반 앙상블 모형의 출력값은 이진 분류 값이며, 성능측도는 5-조각 교차타당성에 의해 생성된 5개의 데이터 셋에 대해 평균을 가지고 얻어진다.
정확도는 전체 데이터 중 실제 목표값과 모형의 예측값이 일치하는 정도를 나타내고 ROC 곡선은 분류모형의 (1-특이도(specificity))를 x축으로 하고 민감도(sensitivity)를 y축으로 한 그래프이다. (1-특이도)를 위양성률(false positive rate)이라 하고 민감도를 진양성률(true positive rate)이라고 한다. ROC 곡선은 분류모형의 결과 값인 사후확률(posterior probability)이 변화할 때 위양성률과 진양성률의 변화를 그래프로 나타낸 것으로 ROC 곡선이 좌측 상단으로 더 위에 위치할수록 좋은 모형이다[15]. ROC 곡선 아래의 면적을 c-통계량이라고 하는데 어떤 모형의 ROC 곡선 아래의 면적이 다른 모형의 면적보다 크면 평균적으로 더 우수한 모형이라 할 수 있다[16].
연구 결과
제안한 딥러닝기반 앙상블 모형의 성능을 평가하기 위해 기존의 단일모형으로 k-근접 이웃, 의사결정나무, 서포트 벡터 머신, 판별분석, 로지스틱 회귀분석과 심층신경망을 고려하였고, UCI 데이터베이스에 있는 WOBC 자료, WDBC 자료를 사용하여 평가하였다. 여기서 WDBC 자료는 표준화, 즉 평균을 빼주고 표준편차로 나누는 작업을 수행 후 사용하였다.
본 논문에서 딥러닝은 H2O 플랫폼을 사용하여 수행하였다. H2O 플랫폼의 성능은 은닉층의 크기와 노드 수, 반복 수 그리고 활성화 함수 등 여러 가지 모수에 의해 영향을 받는다. 여기에서는 H2O 플랫폼에 주어진 기본환경, 즉 은닉층의 수는 2개이고 각 층의 노드는 각각 200개, 200개이고 반복 수(epochs)는 10이고 활성화 함수(activation function)는 Rectifier Linear Unit (ReLU)을 사용하고 있다.
본 연구는 통계 프로그램 R (ver. 3.4.1)을 사용하고 딥러닝은 “h2o” 패키지[17]를 사용하였고, 그리고 k-근접 이웃, 서포트 벡터 머신, 의사결정나무, 판별분석, 로지스틱 회귀분석은 “caret” 패키지[18]의 각각 “knn”, “svmRadial”, “rpart”, “lda”, “glm” 패키지에서 기본옵션을 사용하였다. 여기서 “knn”은 유클리디안 거리(Euclidean distance) 하에서 k=5를 사용하고, “svmRadial”은 래디얼 커널(radial kernel)을 사용하고 WOBC 자료에서 C = 0.25, σ = 0.755, WDBC 자료에서 C = 0.25, σ= 0.0464 그리고 “rpart”는 CART 알고리즘을 사용하여 불순도(impurity)의 측도로서 지니지수(Gini index)를 이용하여 이진분리(binary split)하였다. 참고로, 딥러닝에 많이 사용하는 R 패키지로는 h2o와 deepnet 패키지가 있다. deepnet 패키지는 제한된 볼츠만 머신(restricted Boltzmann machine), 딥 신뢰 망(deep belief network), 스택 오토코더(stacked autoencoders) 등과 같은 다양한 딥 아키텍처(deep architecture)를 제공하나 GPU 지원이 미흡하고 또한 튜닝 파라미터를 제공하고 있지 않아 방대한 데이터 처리용으로 사용하는 것을 권장하지 않는다. 반면에 h2o 패키지는 H2O 플랫폼 상에서 분산 처리가 가능하고, 높은 수준의 사용자 경험을 제공하며 또한 빠른 학습 속도와 많은 튜닝 파라미터를 제공한다.
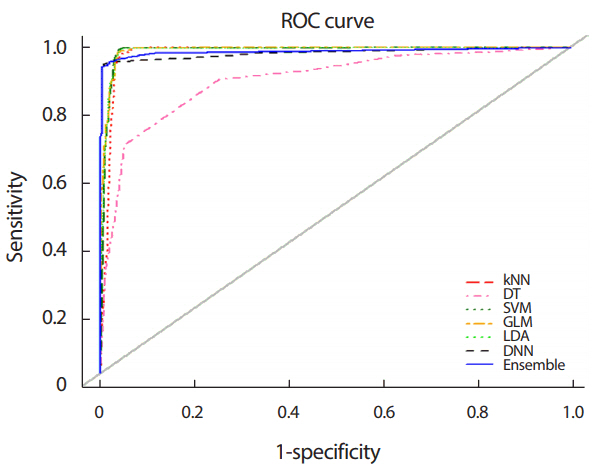
Figure 3은 분류모형을 WOBC 자료에 적용하여 얻은 ROC 곡선들을 나타내고 있다. 여기서 kNN는 k-근접 이웃, DT는 의사결정나무, SVM은 서포트 벡터 머신, GLM은 로지스틱 회귀분석, LDA는 판별분석, DNN은 심층신경망 그리고 Ensemble은 제안한 딥러닝기반 앙상블모형을 나타낸다.
Figure 3으로부터 의사결정나무를 제외한 나머지 모형들의 ROC 곡선들은 왼쪽 위 상단에 위치하고 있어 좋은 성능을 보임을 알 수 있다. 이들 곡선들은 서로 중첩되어 있어서 가시적으로 좋고 나쁨을 구별하는 것은 쉽지 않다. 의사결정나무의 ROC 곡선은 대각 참고선(diagonal reference line)과 가장 가까이 위치하고 있어 성능이 현저히 떨어짐을 보이고 있다.
Table 3은 WOBC 자료에 적용하여 얻은 분류모형의 정확도와 c-통계량을 보여주고 있다. 먼저, 정확도면에서 보면 제안된 딥러닝기반 앙상블모형이 가장 높은 정확도를 나타내고 있고 다음으로 심층신경망, k-근접 이웃 순으로 나타났고, 의사결정나무가 가장 낮은 정확도를 보였다. c-통계량에서 보면 딥러닝기반 앙상블모형이 가장 높고 다음으로 로지스틱 회귀분석, 판별분석, 심층신경망 순으로 나타났고, 의사결정나무가 가장 낮은 c-통계량을 보였다.
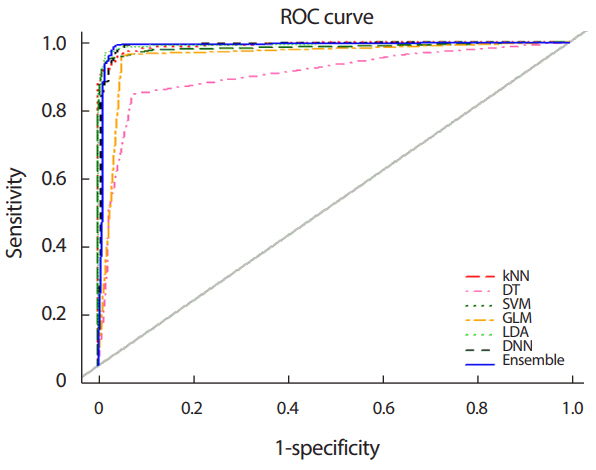
Figure 4는 분류모형을 WDBC 자료에 적용하여 얻은 ROC 곡선들을 나타내고 있다.
Table 4는 WDBC 자료에 적용하여 얻은 정확도와 c-통계량을 보여주고 있다.
Table 4의 정확도면에서 보면 WOBC 자료에서처럼 제안된 앙상블모형이 가장 높고 다음으로 심층신경망, k-근접 이웃 순으로 나타났고, 의사결정나무가 가장 낮은 정확도를 보였다. c-통계량 면에서는 심층신경망이 제안된 앙상블모형보다 약간 높게 나타났고, 다음으로 판별분석, 서포트 벡터 머신 순으로 나타났고, 의사결정나무가 가장 낮은 c-통계량을 보였다.
고 찰
본 연구에서 유방암의 성능향상을 위해 제안된 딥러닝기반 앙상블 방법은 두 단계에 걸쳐 이루어지고 있다. 첫 번째 단계에서 사용된 스태킹 앙상블은 같은 종류의 모형(homogeneous models)을 앙상블한 배깅, 부스팅과는 다르게 서로 다른 모형들을 결합하여 단일 모형에 비해 성능을 향상시키는 방법이다. 다른 앙상블처럼 첫 번째 단계에서 최종 분류를 할 수 있으나 보다 정확한 유방암 분류를 위해 추가적으로 딥러닝을 적용하여 최종분류하고 있다.
현재 딥러닝을 위한 여러 가지 플랫폼들이 개발되고 있다. 대표적인 플랫폼에는 MXNet, Caffe, TensorFlow, Theano, Torch, H2O 등이 있다. 본 논문에서는 세계 최고의 오픈소스 플랫폼인 H2O 플랫폼을 사용하고 있다. H2O 플랫폼은 일반적인 개발 환경(파이썬, 자바, 스칼라, R), 빅데이터 시스템(하둡, 스파크), 그리고 다양한 데이터 소스(HDFS, S3, SQL, NoSQL)를 통해 머신러닝 알고리즘에 대한 액세스를 제공한다. 그리고 H2O 플랫폼은 데이터 수집, 모형 구축, 그리고 각종 예측을 제공하기 위한 엔드 투 엔드 솔루션으로 개발되어 있어 사용가능하다. 본 논문에서는 H2O 플랫폼의 주어진 기본환경, 즉 자료에 상관없이 주어진 모수, 즉 은닉층의 수, 은닉 노드의 수, 반복 수, 활성화 함수 등의 기본값을 사용하고 있다. 따라서 딥러닝의 성능은 H2O 플랫폼의 최적의 모수를 추정함으로서 개선시킬 수 있다.
결 론
여성의 유방암 발병률은 지속적으로 증가하고 있으며, 현대 의학 기술의 발달로 인해 조기 발견율이 높아지고 환자 삶의 질을 향상시키는 치료방법들이 개발되면서 검진의 비중 역시 늘어나고 있다. 최근 국가 암검진에서 유방암의 진단 정확도가 너무 낮다는 문제가 제기되는 가운데 의사로 하여금 진단 정확도를 높일 수 있는 보조 수단으로 통계적 분류방법이 중요시되고 있다.
딥러닝은 머신러닝의 한 분야로 영상 인식, 음성 인식 등, 다양한 분야에서 획기적인 결과를 내면서 큰 주목을 받고 있다. 본 연구에서는 유방암 분류성능 향상을 위해 딥러닝기반 앙상블 모형을 구축하고 기존의 단일 모형들과의 성능을 비교하였다.
본 연구에서 제안된 딥러닝기반 앙상블은 두 단계에 걸쳐 이루어졌다. 첫 번째 단계에서는 형태가 다른 5가지의 기본 모형, 즉 k-근접 이웃, 서포트 벡터 머신, 의사결정나무, 판별분석, 로지스틱 회귀 모형을 가지고 스태킹 앙상블 수행한 후 두 번째 단계에서는 딥러닝을 적용하여 분류성능을 향상시켰다.
본 논문에서는 딥러닝기반 앙상블의 성능을 평가하기 위해 UCI의 유방암 자료에 대해 기존의 분류방법인 k-근접 이웃, 의사결정나무, 서포트 벡터 머신, 판별분석, 로지스틱 회귀분석과 성능평가 측도인 정확도, ROC 곡선 그리고 c-통계량을 가지고 비교분석하였다.
실제 WOBC 자료와 WDBC 자료에서 성능 실험 결과 ROC 곡선에서 의사결정나무를 제외하고는 제안된 딥러닝 앙상블을 포함한 모든 방법이 좋은 성능을 보였고, 정확도 면에서 WOBC 자료와 WDBC 자료 모두에서 제안된 앙상블모형이 가장 높고 다음으로 심층신경망, k-근접 이웃 순으로 성능을 보였다. c-통계량 면에서 WOBC 자료에서는 제안된 앙상블모형이 가장 높고 다음으로 로지스틱 회귀분석, 판별분석 순으로 나타났고, WDBC 자료에서는 심층신경망, 제안된 앙상블모형 순으로 나타났으며 의사결정나무는 가장 성능이 떨어지는 것으로 나타났다.
본 연구에서 딥러닝은 H2O 플랫폼의 주어진 기본환경하에서 수행하였다. 향후 연구에서는 주어진 자료로부터 H2O 플랫폼의 최적의 모수를 추정함으로서 탁월한 성능을 갖는 딥러닝 앙상블모형을 개발하고자 한다.