서 론
최근 딥 러닝 기법을 적용한 분류 및 예측 모델은 각종 분야에서 우수한 결과를 도출하고 있고, 그에 따라 많은 각광을 받고 있다. 그러나 그 예측 결과에 대한 각 입력변수들의 기여도를 알 수 없기 때문에 블 랙박스 모델로도 불리며 모델 신뢰성의 문제를 안고 있다[1,2]. 이를 해결하고자 최근 딥 러닝 모델로 얻은 결과에 대해 시각화, 설명 및 해석을 가능하게 하는 설명 가능한 인공지능(eXplainable Artificial Intelligence, XAI) 기법들이 연구되고 있다[3]. XAI 기법은 미국의 국방고등연구계획국(Defense Advanced Research Projects Agency)에서 중요한 안건으로 선정될 만큼 주목받고 있다[4].
딥 러닝 기법을 적용해 데이터를 학습한 모델에 XAI 기법을 적용하고 시각화를 하면 결과에 대한 해석력을 높일 수 있다. 최근 연구된 XAI 기법들 중 Local Interpretable Modelagnostic Explainations (LIME) [5]과 Gradient-weighted Class Activation Mapping (Grad-CAM) [6]이 가장 널리 쓰이고 있다. 또한, Feng et al. [7]은 다중작업학습 증강신경망(Augmented neural network with multi-task learning, ANN-MTL)으로 변수 중요도 추출에 관한 연구를 하였다. 추출된 변수 중요도를 통해 각 입력변수들이 결과에 얼마나 영향을 미치는지를 알 수 있다.
의학 분야에서도 마찬가지로 딥 러닝 기법을 적용함으로써 환자에게 높은 정확도를 갖춘 결과를 제공할 수 있으나, 모델의 투명성 결여는 결정적인 단점이 될 수 있다. 따라서 의학 분야에 적합한 XAI 기법들이 다양하게 연구되고 있다[8,9]. Lamy et al. [8]은 실제 유방암 데이터를 기존의 사례 기반 추론(Case-Based Reasoning, CBR) 방법에 자동 알고리즘을 사용하여 시각적인 정보를 제공하거나 시각적인 추론을 위해 사용자의 인터페이스에 시각적으로 제시 될 수 있는 새로운 CBR 방법을 제안하였다. 이는 쿼리와 유사한 사례 간의 유사성을 나타내는 시각적 인터페이스를 통해 결과를 설명할 수 있다는 장점이 있다. 같은 맥락으로 Sabol et al. [9]은 조직 병리학적 이미지로부터 유방암 검출을 위해 의학적 영역에서 의미적으로 설명 가능한 분류기인 Cumulative Fuzzy Class Membership Criterion (CFCMC)를 제안하였다. 그들은 CFCMC와 일반적으로 쓰이는 3가지 분류기인 Convolutional Neural Network (CNN), Stacked Auto-Encoder, Deep Multi-Layered Perceptron 을 비교하였다. CFCMC는 결과에 대한 시각적인 정보를 제공함으로써 오분류 가능성에 대한 의미적인 설명을 가능하게 함을 알 수 있었다.
본 논문에서는 인공지능 기법을 사용하여 의학 분야에서의 정형·비정형 데이터를 분석한 결과에서 변수 중요도를 기반으로 시각화하는 방안에 대해 살펴본다. 첫 번째는 사망 유무에 대한 중환자실 환자들의 상태를 측정한 정형 데이터이다. 사람들은 환자가 중환자실 내에서 사망했다는 결과보다 왜 사망을 했는지에 대한 이유에 주목하기 때문에 수치적인 근거와 함께 올바른 예측 결과 정보를 제공하고자 한다. 중환자실 데이터 중 환자 유형을 나타내는 변수를 층화 변수로 삼고, 각 환자군마다 ANN-MTL과 머신러닝 기법들을 데이터에 적용한 후 각 입력변수들의 중요도를 추출하여 기법별로 결과에 중요한 영향을 미치는 변수들이 무엇인지 비교하였다. 나아가 추출된 변수 중요도를 시각화하여 결과에 영향을 미치는 설명변수들을 종합적으로 판단할 수 있게 하였다.
두 번째는 일곱 가지 종류의 피부암을 분류하기 위한 이미지 데이터이다. 일반적으로 환자들이 피부암의 종류를 육안으로 구별하는 것은 어렵다. 이러한 이유로 이미지 분류를 위한 CNN 구조 모델에 이미지 데이터를 적용한 후, 해당 모델에 LIME과 Grad-CAM을 적용하여 많은 픽셀들 중 분류 결과에 영향을 미치는 픽셀들의 집합은 무엇인지에 대해 중요한 피쳐(feature)들의 시각화에 관해 연구하였다. 그리고 시각화된 결과를 바탕으로 피부암 종류에 따라 어떤 부분이 좋은 분류 결과를 도출하는데 중요한 영향을 미쳤는지에 대한 해석을 제공하고자 한다.
연구 방법
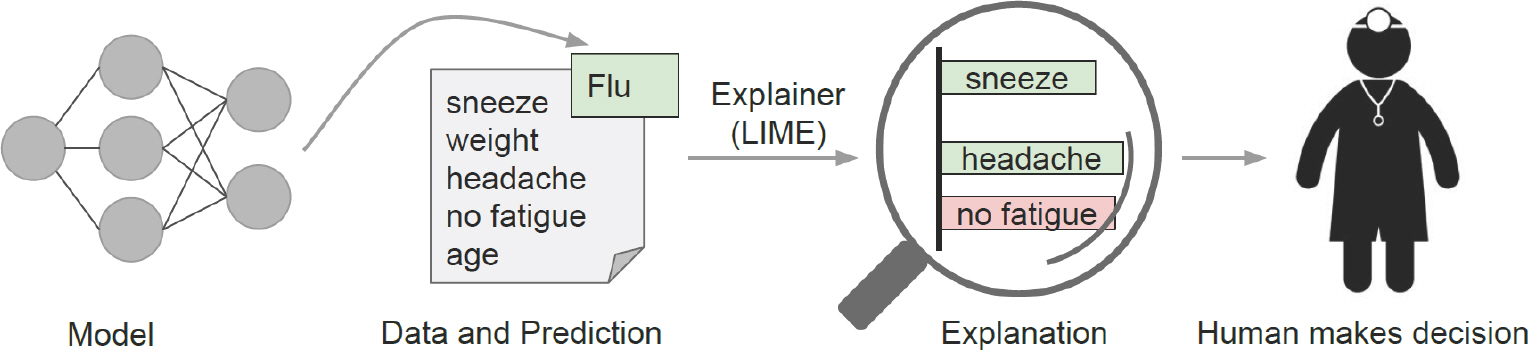
Ribeiro et al. [5]은 설명하고자 하는 데이터 위주로 국소적인 범위의 데이터에 근사하여 분류기 또는 회귀 예측을 설명할 수 있게 하는 알고리즘인 LIME을 제안하였다. 그들은 결과 신뢰의 문제를 각각 예측 결과의 신뢰 문제와 모형의 신뢰 문제로 정의하였다. 예측 결과의 신뢰 문제란 개별의 예측 결과를 통한 의사결정 가능 여부이고, 모형의 신뢰 문제는 학습 데이터에 과적합 되는 경우가 많으므로 모형 자체를 신뢰할 수 있는지에 대한 것이다. Figure 1으로 예를 들면, 예측 결과의 신뢰도가 높은 의사가 환자에게 어떤 요소들로 인해 감기에 걸렸는지를 신뢰도가 높은 모델을 통해 나온 결과로 설명한다면 전체적인 진단 과정 및 결과에 대한 신뢰도를 높일 수 있다는 것이다.
블랙박스 모델들을 해석하기 위해서는 실제로 모델에 입력되는 값 인 피쳐는 사람이 해석할 수 있는 데이터 형태로 표현되어야 한다. 이 를 해석가능한 데이터 표현(interpretable data representation)이라 한다. 예를 들어 텍스트 데이터의 경우 숫자의 의미를 알기 힘든 임베딩 벡 터가 아닌 단어의 유무를 나타내는 원핫 인코딩(one-hot encoding), 이 미지 데이터의 경우 픽셀의 유무를 나타내는 이진 벡터를 뜻한다.
원 데이터를x∈Rd 라고 할 때, 해석가능한 데이터 표현인x∈{0,1}d' 으로 나타낸다고 하자. 해석 가능한 데이터 표현으로 원 데이터를 변환 하는 작업은 디리클레 할당(Dirichlet allocation), 주성분 분석 등을 사 용하여 높은 차원을 갖는 복잡한 데이터의 한 포인트에 대하여 변수 변환을 한 뒤, 변환된 변수를 사람이 얼마나 잘 원래 데이터와 같은지 판단할 수 있는가에 대한 여부를 실험을 통하여 변수 변환법을 선정 하고 해석 가능하게 변형하는 방법으로 사용한다. 본 연구에서는 해석 가능하게 데이터를 표현하기 위해서 데이터의 차원이 변할 수 있으므 로 차원을 d´로 표기한다. 위에서 설명한 바와 같이 LIME은 설명하고 자 하는 데이터 위주로 국소적인 범위의 데이터에 근사하기 때문에 국 소의 공간에서 설명력을 높일 수 있다. 하지만 데이터 포인트의 전체적 인 충실도(fidelity)를 고려하게 되면 설명력과 국소적 충실도가 작아지 는 단점이 생기며 이를 충실도-해석력 트레이드오프라고 한다. 따라서 국소적 충실도와 설명력을 충족시키기 위한 설명자(explainer)인 g는 다음과 같이 찾을 수 있다.
우선 정의된 비용함수 L은 범위 인지 로스(Locality-aware loss)로, 다음과 같은 계산식을 갖는다.
또한 모델 f는 f: R d → R의 함수로 데이터를 학습한 모형이자 블랙박스 모델이다. 예측 결과의 설명자인 g는 g∈ G로 정의되며 G는 선형 회귀모델, 의사결정 나무와 같이 설명 가능한 모델들의 집합이다. π x는 설명하고자 하는 데이터인 x와 다른 데이터인 z 간의 유사도를 나타내는 유사도 측도이고, Ω(g)는 모형의 복잡도를 나타낸다. 유사도 측도는 대표적으로 벡터로 표현된 데이터들의 유클리디안 거리(Euclidean Distance), 맨해튼 거리(Manhattan Distance), 코사인 유사도(Cosine Similarity) 등으로 측정되며, 모형의 복잡도란 특정 모델이 갖는 파라미터의 수 등으로 결정되는 모델의 크기에 대한 측도이다.
이러한 국소적 설명자를 생성하기 위해는 설명하고자 하는 데이터를 기준으로 주변의 데이터들을 샘플링 해야 한다. 이 때 LIME은 f를 특정한 모형으로 가정하지 않고도 국소적 설명자를 생성하여 설명을 가능하게 하는 것이 목적이다. x ' ∈ { 0 , 1 } d ' x ' ∈ { 0 , 1 } d ' z ∈ R d
Grad-CAM
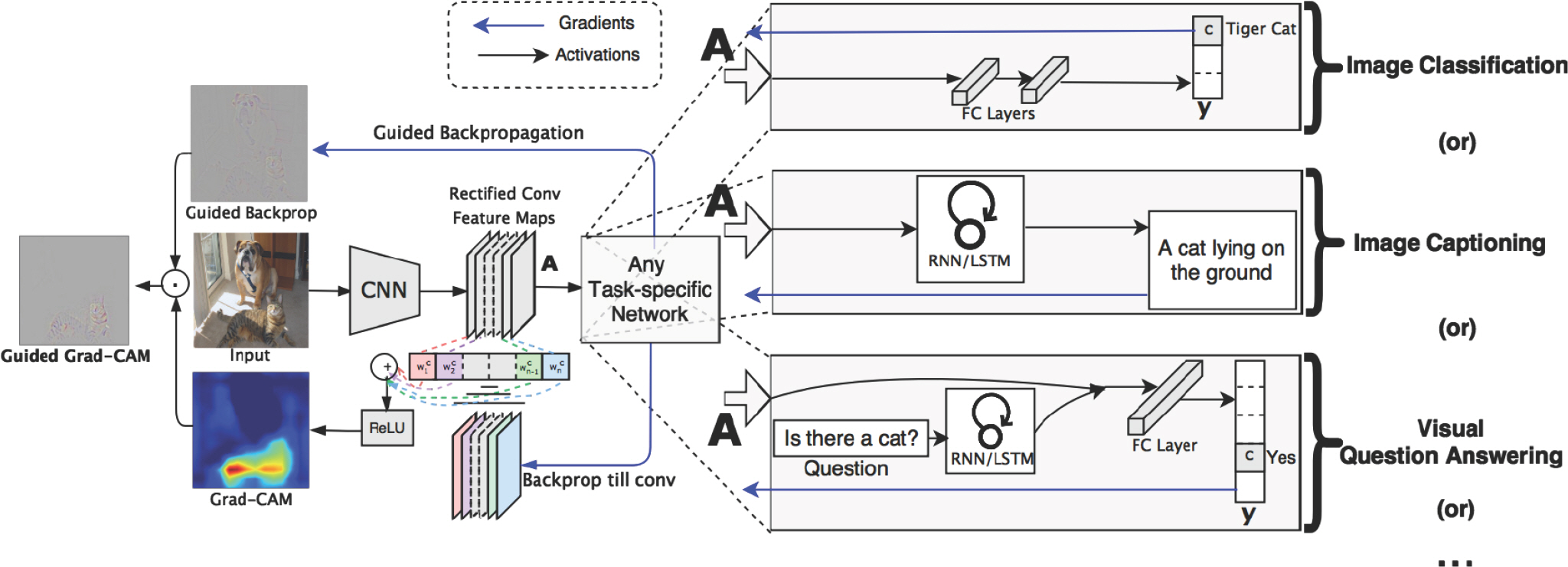
Selvaraju et al. [6]은 Class Activation Mapping (CAM)을 구할 때 예측 이미지에서 중요한 부분을 강조하는 지역 맵(local map)을 생성하기 위해 마지막 합성곱 층으로 흐르는 정답 클래스에 대한 기울기를 이용하는 Grad-CAM을 제안하였다. CAM은 이미지 분류 task에서 관심 있는 영역을 확인할 수 있도록 식별 가능 부분을 히트맵 형태로 나타내는 딥 러닝 시스템 해석 방법 중 하나로서 Zhou et al. [10]이 제안하 였다. Figure 2에서는 Grad-CAM 기법의 구조를 보여주고 있다. Grad-CAM 기법은 이미지 분류, 이미지 캡셔닝, 시각 질의응답 task에 대해서 적용할 수 있으며 본 논문에서는 이미지 분류 task에 적용하였다.
아래는 분류 문제에 있어서 클래스를 구분하는데 있어서 중요한 부분을 표시해 주는 맵(class-discriminative localization map)인 Grad-CAM L c G r a d - C A M ∈ R u × v a k c
Figure 2.
Architecture of Grad-CAM (Gradient-weighted Class Activation Mapping) (Selvaraju et al., 2017).
여기에서, y c는 소프트맥스 함수를 거치기 전 단계의 정답 클래스 c에 대한 레이블 y의 점수이며 역전파(backpropagation) 알고리즘을 거쳐 k번째 특성맵(feature map)의 (i,j)위치에 있는 A i , j k a k c
이렇게 얻은 가중치를 통해 정답 클래스 c에 대한 k번째 특성 맵 A k의 중요도를 포착할 수 있다. k개의 각 뉴런의 중요도 가중치 a k c
다중작업학습 증강신경망
Feng et al. [7]은 설명변수들의 다양한 부분집합에 대해 효율적인 계산이 가능한 손실함수와 ANN-MTL을 새롭게 제안하였다. 그들은 데이터를 적합할 때 데이터 생성 메커니즘(data-generating mechanism)의 함수로서 변수 중요도를 고려하는 것이 특정 예측 알고리즘의 사용보다 유용하다고 하였다. 이러한 원리를 기반으로 신경망을 이용한 예측 모델을 세울 때 변수 중요도 추정량을 도출할 수 있는 효율적인 방법을 제시하고 있다. 그들은 단일의 증강신경망으로도 설명변수들의 다 이 가능함을 보였다[7].
어떤 특정한 분포 P에서 도출된 n개의 독립적인 관측치 O1, O2, …, O n가 있다고 가정한다. 그리고 각 관측치 Oi는 설명 변수와 종속 변수인 (Xi, Yi)의 형태로 이루어져 있다. 이때 Xi는 입력변수의 행벡터로 Xi: =(Xi1, Xi2, …, Xip)∈ R p이고, Yi는 관측치로 Yi∈ R이다. 그리고 분포 P를 따르는 s⊆{1, …, p}에 속하는 입력변수 { Xi} i∈ s의 중요도를 입력변수들의 전체집합과 부분집합 s를 제외한 축소 집합의 조건부 평균을 통해 측정하고자 한다. 입력변수들의 전체집합으로 얻은 조건부 평균은 µ P(x)라 하고 부분집합 s를 제외한 축소 집합의 조건부 평균은 µ P,s(x)라고 할 때 다음과 같이 정의한다.
두 값 간의 차이가 크면 입력변수들의 부분집합 s의 중요도는 큰 것이고 작으면 s의 중요도는 작다. 이를 통해 { Xj} j∈ s의 중요도를 나타내는 지표는 다음과 같다.
이때 n개의 관측치 { ( X ( i ) , Y ( i ) ) } i = 1 n µ ^ µ ^ s P ^ n
위 추정량을 구하는 식은 부분집합 s의 중요도 ψ0,s를 추정하기 위해 P0와의 관련 구성요소를 추정한 µ ^ µ ^ s ψ ^ n , s
이 때 A i , n , s : = 2 Y i - µ ^ ( X ( i ) ) - µ ^ s ( X ( i ) )
ANN의 모든 모수들의 집합이 Θ(q)이고 입력층의 노드가 q개, 출력층의 노드가 1개라 하자. 이 때 모수 θ∈Θ(q)는 f(· θ)로 표현한다. n개의 관측치이며 { ( x ( i ) , y ( i ) ) } i = 1 n
ANN 구조에서 입력 층은 각각 입력변수 task인 xi와 조건부 평균 task인 mi로 이루어져 있다. 모델의 핵심은 이러한 입력 층의 구조로 인해 위의 두 가지 task로 동시에 학습하는 다중작업학습을 통하여 조건부 기댓값을 추정함으로써 변수 중요도 값을 구할 수 있다는 것이. 이진벡터 e s∈{0,1} p로 입력 노드의 개수를 입력변수 개수의 2배만큼 늘인다. p개의 입력변수 X1, …, Xp가 모두 주어졌을 때, 조건부 평균 E(Y| X1, …, Xp)를 얻으려면 m1, …, m p에 모두 0을 넣는다. 그리고 관심 있는 입력변수를 Xj, 1≤ j≤ p로 하고 Xj를 제외한 나머지 입력변수들이 주어졌을 때, 조건부 평균 E(Y| X1, …, Xj-1, Xj+1, … Xp)을 얻으려면 m j에 1을 넣고 나머지 m j들에는 0을 넣는다. 이렇게 두 가지 task로 인해 발생하는 모델의 multi-loss는 다음과 같이 정의하고 이를 최소화하는 θ를 찾는다.
여기에서 Ws는 실수로 이루어진 공간인 R| s|에 속한 확률변수이다. Feng et al. [7]은 실험을 통해 확률적 경사하강법(stochastic gradient descent)의 매 단계에서 적합한 Ws를 찾아 대체 하는 것이 loss를 더욱 줄일 수 있는 면에서 나음을 보였다. 그러나 본 연구에서는 머신러닝 기법과도 비교하기 때문에 고정된 값으로 Ws를 대체하였다. { ξ ( x , w ; s ) } ( - s ) = x ( - s ) ( i )
따라서 모든 경우의 조건부 기댓값을 추정하는데 있어 손실함수 값의 합을 최소화하도록 이 증강신경망으로 학습한다. 그리고 해당 모델을 이용해 조건부 기댓값을 구함으로써 변수 중요도 값을 계산할 수 있다.
연구 결과
중환자실 데이터에 대한 변수 중요도의 시각화
데이터 설명 및 실험 목적
본 연구의 중환자실 수치형 데이터는 PhysioNet/CinC Challenge 2012로부터 공개되었다[12]. 중환자실 환자들의 사망률 예측 방법의 개선을 위해 입원했던 4,000명의 환자들을 대상으로 5개의 환자 고유 변수를 제외한 최대 36개의 변수에 대해 48시간 동안 시간마다 측정하였다. 이를 통해 각 변수의 수치 변화에 따라 위험하거나 안정적인 환자를 조기에 식별하는데 도움이 될 수 있다. 환자 고유변수는 환자번호, 나이, 성별, 키, 몸무게이다. 그 외 36개의 변수 중 중요도 측정에 사용된 변수는 Table 1에 제시하였다.
Table 1.
Variable types and names forintensive care unit (ICU) data
또한 응급실을 내원한 환자들의 증상에 따라 분류한 값(Intensive Care Unit, ICU 타입)을 나타내는 변수를 층화 변수로 사용하였다. 환자군마다 응급실 내 사망에 대해 작용하는 변수들이 차이가 있고 그 결과로 머신 러닝 기법들의 변수 중요도로 나타날 것이라고 예상을 하였기 때문이다. ICU 타입은 총 4가지로, 1은 관상 동맥계 중환자실, 2는 심장계 중환자실, 3은 내과계 중환자실, 4는 외과계 중환자실이다. 사용된 변수 중 하나인 인공호흡기 Mechventialtion (MechVent)는 차고 있지 않은 상태인 0이 정상임을 뜻한다. 48시간 동안 2번 이상의 측정값을 가진 변수에 대해서는 이를 그대로 사용하지 않고 각 변수의 최솟값, 최댓값, 평균값, 합계, 변화량, 마지막 수치의 추가 변수를 생성하 였으며, 본 연구에 쓰인 변수는 총 55개이다. 더 나아가, 각 변수의 최솟값, 최댓값 등을 모두 사용하여 머신 러닝 기법에 적용한다면 변수 간 상관관계가 있는 경우 변수 중요도를 측정하는 데 있어서 잘못된 해석을 도출할 가능성이 매우 크다. 따라서 각 변수의 대푯값을 설정하기 위해, 최솟값, 최댓값, 평균값, 합계, 변화량, 마지막 수치를 모두 포함한 55개의 변수들에 대한 분산팽창지수를 계산하여 다중공선성이 일어나지 않도록 변수 선택법을 적용하였다. 선택된 변수는 총 27개였으며 각 변수 명과 계산된 분산팽창지수를 Table 2에 제시하였다. 타겟변수는 중환자실 내에서의 사망 여부이고, 4,000개의 데이터 셋을 scikit-learn api [13]의 함수 중 train_test_split을 사용하여 랜덤하게 훈련 데이터 셋 3,200개, 테스트 데이터 셋 800개로 나누어 ANN-MTL로 학습하였다.
Table 2.
Selected variable types and their variance inflation factor (VIF) for intensive careunit (ICU) data
본 논문에서는 ICU 데이터를 중환자실 타입으로 분류한 뒤 머신러닝 기법인 랜덤 포레스트, 엑스트라 트리, 그래디언트 부스팅, Xgboost 로도 학습하여 각 기법별로 응급실 내원 환자군에 따라 사망 여부에 영향을 미치는 변수들이 무엇인지, 그 변수들의 중요도는 어느 정도인 지 비교해보았다. 나아가 변수 중요도의 값들을 시각화를 하였으며 그 결과들을 종합적으로 판단하여 변수 중요도에 대한 결론을 내리고 결과에 대한 해석을 하였다.
실험 결과
분산팽창지수를 고려하여 선택된 27개의 중환자실 데이터 설명변수를 신경망 기반의 ANN-MTL과 랜덤 포레스트, 엑스트라 트리, 그래디언트 부스팅, Xgboost에 적용한 후 각 기법별 변수 중요도의 산출 기준이 다름을 고려하여 비율로 변환하였다. 총 4개의 중환자실 환자군에 각각 기법들을 적용하였으며 이는 Tables 3에서 Table 6과 같다.
Table 3.
Variable importance (%) based on different methods for intensive care unit (ICU) data of coronary artery intensive care unit
Table 4.
Variable importance (%) based on different methods for intensive care unit (ICU) data of Cardiac intensive care unit
Table 5.
Variable importance (%) based on different methods for intensive care unit (ICU) data of internal medicine intensive care unit
Table 6.
Variable importance (%) based on different methods for intensive care unit (ICU) data of surgical intensive care unit
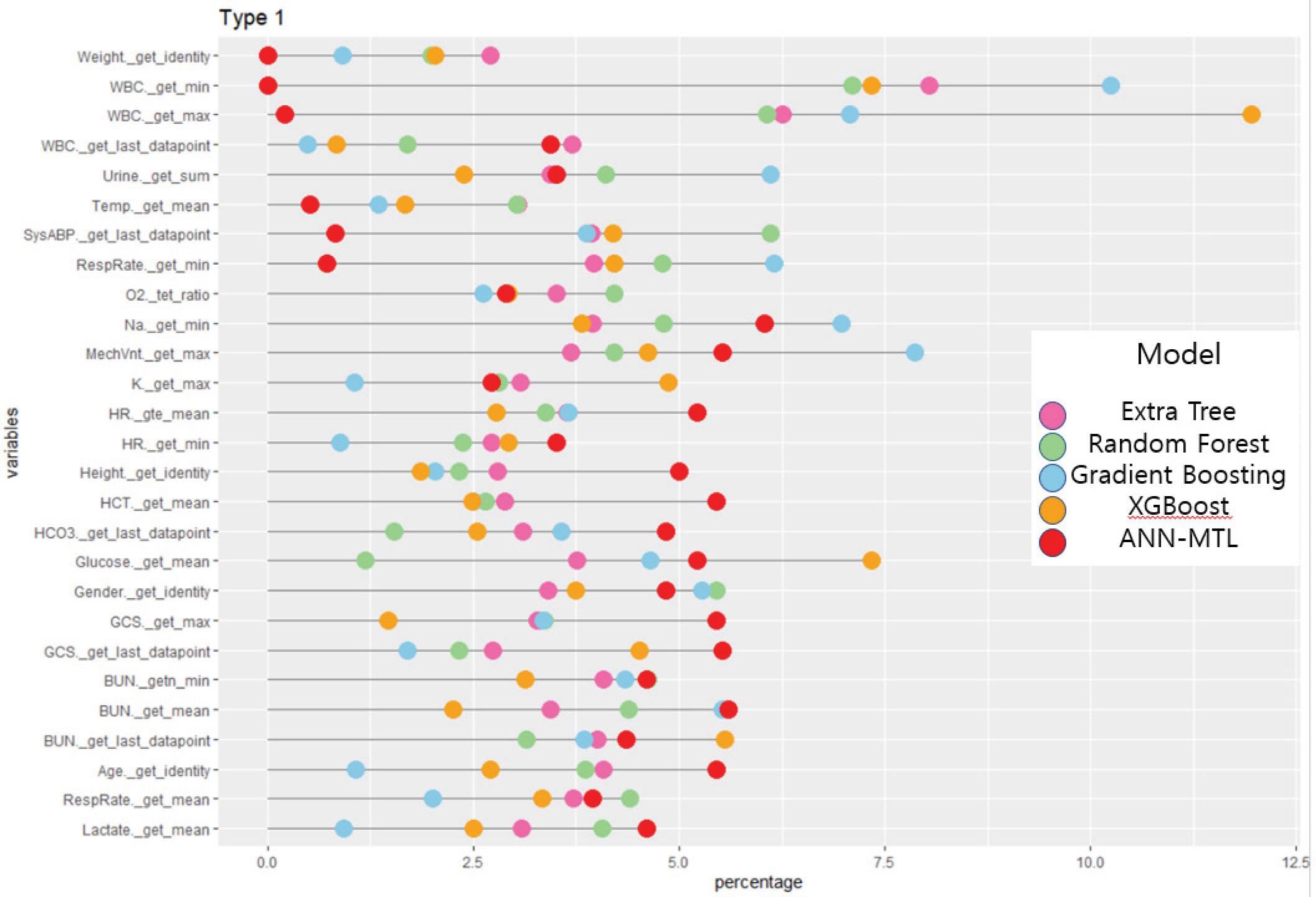
첫 번째 중환자실 타입인 관상 동맥계 중환자실의 경우, 랜덤포레스트, 엑스트라 트리, 그래디언트 부스팅의 기법들에서 백혈구의 수를 나타내는 단위의 변수인 WBC의 최솟값이 가장 중요한 변수로 공통적으로 나타났다. Xgboost의 경우도 또한 두 번째로 높은 변수로 나타나 관상 동맥계 중환자실의 경우 사망 여부에 백혈구의 최소 숫자가 가장 중요하게 작용한다는 것을 확인할 수 있었다. 또한 ANN-MTL의 경우 나트륨의 최솟값 변수인 Na._get_min 변수가 약 6.0%의 변수 중요도 비율로 가장 높게 나왔다.
두 번째 중환자실 타입인 심장계 중환자실의 경우, 관상 동맥계와 비슷한 결과를 보였다. 랜덤 포레스트, 엑스트라 트리, 그래디언트 부스팅, Xgboost 모두 WBC의 최솟값 변수가 가장 중요한 변수로 작용했음을 알 수 있고, 그래디언트 부스팅의 경우 17.5% 이상의 중요도를 보이며 가장 높은 변수 중요도를 기록했다. ANN-MTL의 경우엔 중탄산이온의 마지막 수치가 중환자의 사망 예측에 있어 가장 중요한 변수로 나타났다. 약 9.4%의 변수 중요도를 보였으며 두 번째로 높은 변수는 환자 의식 수준의 마지막 측정값인 GCS._get_last_datapoint로 약 6.3%로 나타났다.
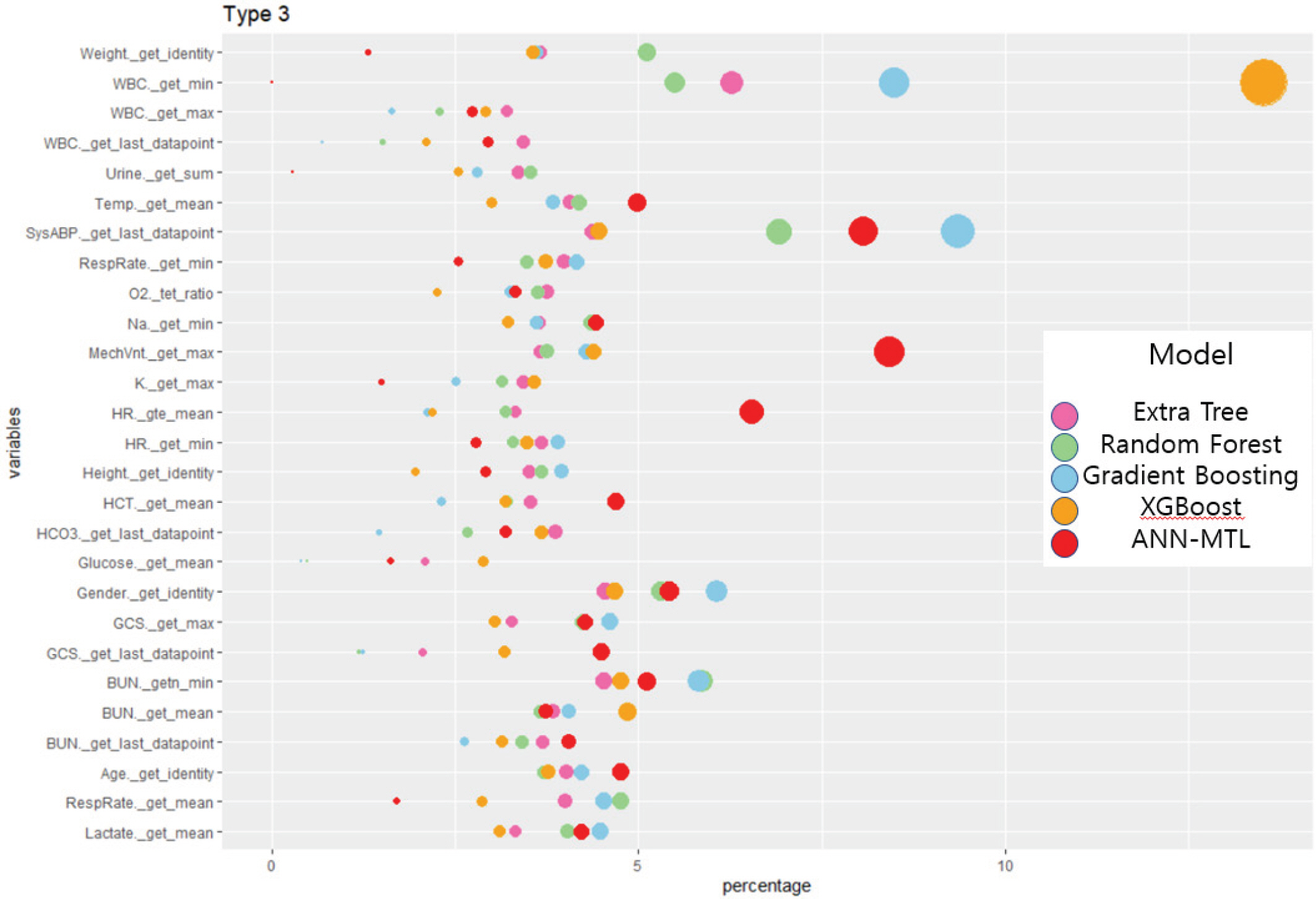
세 번째 중환자실 타입인 내과계 중환자실은 엑스트라 트리와 Xg-boost의 경우 WBC의 최솟값이 가장 중요하게 작용하였고. 각각 6.2%와 13.2%로 나타났다. 랜덤 포레스트와 그래디언트 부스팅은 동맥 혈압인 SysABP의 마지막 기록 변수가 각각 약 6.9%와 9.3%, ANN-MTL 의 경우는 인공 호흡기의 여부인 MechVnt._get_max의 값이 약 8%로 중환자의 사망 예측에 가장 중요하게 작용한 변수로 계산되었다.
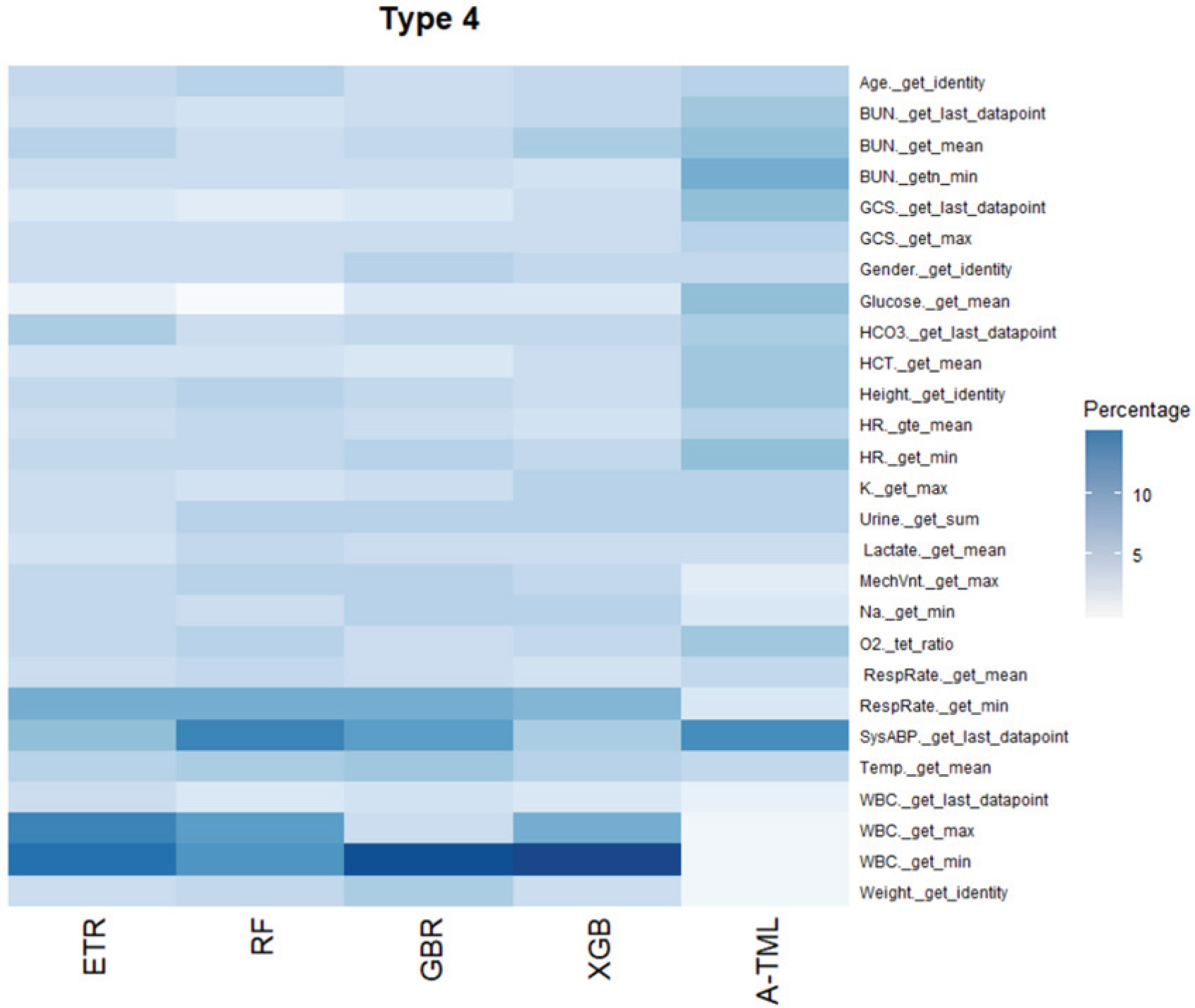
네 번째 중환자실인 외과계 중환자실의 경우도 엑스트라 트리, 그래디언트 부스팅, Xgboost 3가지 모델에서 WBC의 최솟값이 각각 8.1%, 16.8%, 14.3%로 가장 큰 변수 중요도 값을 나타내었다. 또한 WBC 가장 큰 값인 WBC._get_max 변수도 랜덤 포레스트, 엑스트라 트리, Xgboost 세 개의 모델에서 두 번째로 큰 변수 중요도를 보여 외과계 중환자의 경우 백혈구의 수가 사망 예측에 가장 큰 비중을 차지하는 것을 확인할 수 있었다. ANN-MTL의 경우엔 동맥 혈압의 마지막 측정치인 Sys-ABP._get_last_datapoint가 약 8.9%로 중환자의 사망을 예측하는 데 가장 큰 변수 중요도 값으로 나타났다.
4가지 중환자실 유형에서 머신 러닝 기법들에 공통적으로 가장 큰 변수 중요도를 갖는 변수로 자주 선별된 것은 백혈구 수치이다. 백혈구의 수치는 광범위한 급성 또는 만성 질환의 지표로 널리 사용되는 것으로 알려져 있기 때문에[14], 혈관과 관련이 있는 관상 동맥계와 심장계 중환자실의 경우와 내과계, 외과계 중환자실 모두 사망 예측에 중요한 변수로 나타난 것이 타당하다고 보인다.
또한 총 4가지의 중환자실 타입별 비율로 변환한 변수 중요도를 통계 프로그램 R의 ggplot2 패키지[15]를 사용하여 다양한 형태로 시각화 하였다. 첫 번째와 두 번째 응급실 유형인 관상 동맥계와 심장계 중환자실은 Figure 4와 Figure 5로 롤리팝 플랏으로 나타내었다. 각 Figure의 x축은 변수 중요도의 비율이며 y축은 설명변수들이고 색깔은 변수 중요도를 비교한 각 기법이다. 또한 세 번째 유형인 내과계 응급실은 버블 차트를 사용하여 기법별로 변수 중요도에 따른 크기로 나타내었으며 Figure 6에서 확인할 수 있다. Figure 7은 네 번째 유형인 외과계 응급실의 히트맵으로, 큰 변수 중요도를 가질 수록 어두운 색으로 나타난다. 시각화한 그림들을 통해 각 기법마다 중요한 변수가 무엇인지 한 눈에 파악할 수 있었기 때문에 변수 중요도를 추출하여 이를 바탕으로 시각화한다는 것은 매우 중요하고 유용하다.
피부암 이미지 데이터를 활용한 피쳐 중요도의 시각화
데이터 설명 및 실험 목적
두 번째로 사용한 데이터인 피부암 이미지 데이터는 Tschandl et al. [16]의 Human Against Machine with 10000 training images (HAM10000) 데이터 셋이다. HAM10000 데이터 셋은 총 10,015장이며 이미지 한 장당 크기는 크기는 600×450×30이다. 피부암의 종류는 광선각화증(akiec), 기저세포암(basal cell carcinoma, bcc), 지루각화증(bkl), 피부섬유종(dermatofibroma, df), 악성흑색종(melanoma, mel), 비정형색소모반(Melanocytic nevi, nv), 혈관종(vascular lesion, vasc)으로 총 7가지이다. 각 병변별로 특징이 있지만 일반 환자들이 구별하기엔 무리가 있으며 초기에는 점과 비슷하게 보이기도 한다. 그러나 병변이 진행됨에 따라 위험도 높은 범주로 분류될 가능성이 있다. 또한 nv와 mel은 매우 비슷한 모양을 보이기도 한다. 그러므로 병변을 잘 분류하고 LIME과 Grad-CAM으로 시각화함으로써 피쳐 중요도를 나타내어 분류한 결과에 대한 설명을 용이하게 하고자 본 실험을 수행하였다.
실험 결과
다음은 피부암 이미지 데이터에 관한 실험 결과이다. 7가지 병변별로 LIME과 Grad-CAM 기법 적용 후의 이미지와 함께 생김새의 특징 을 설명한다.
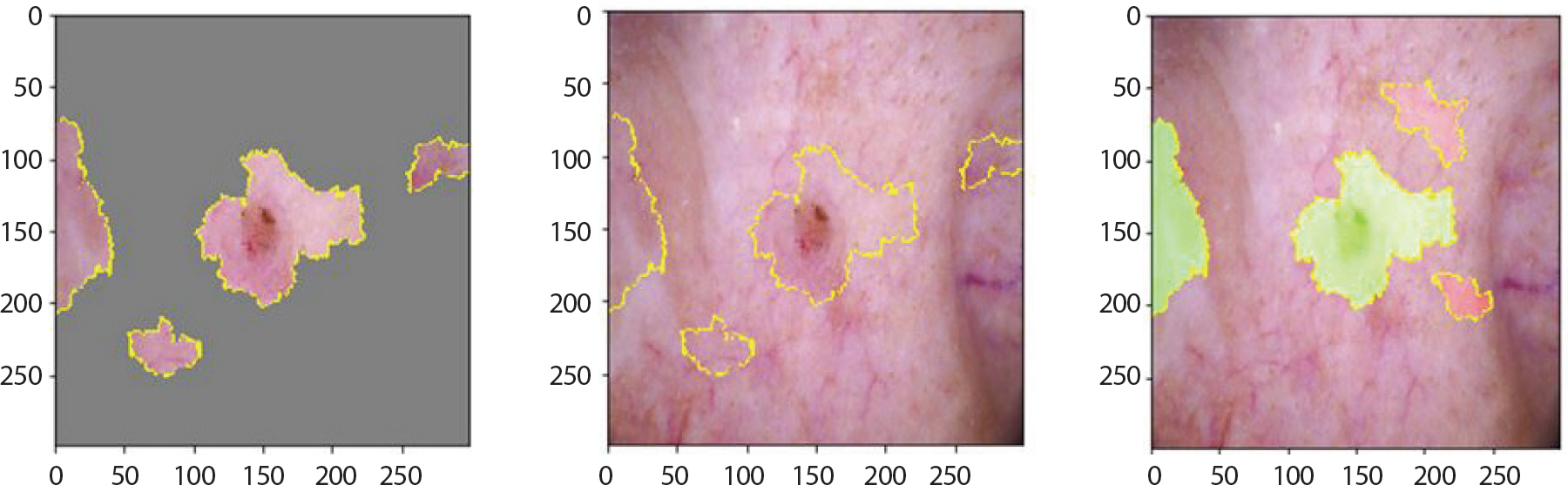
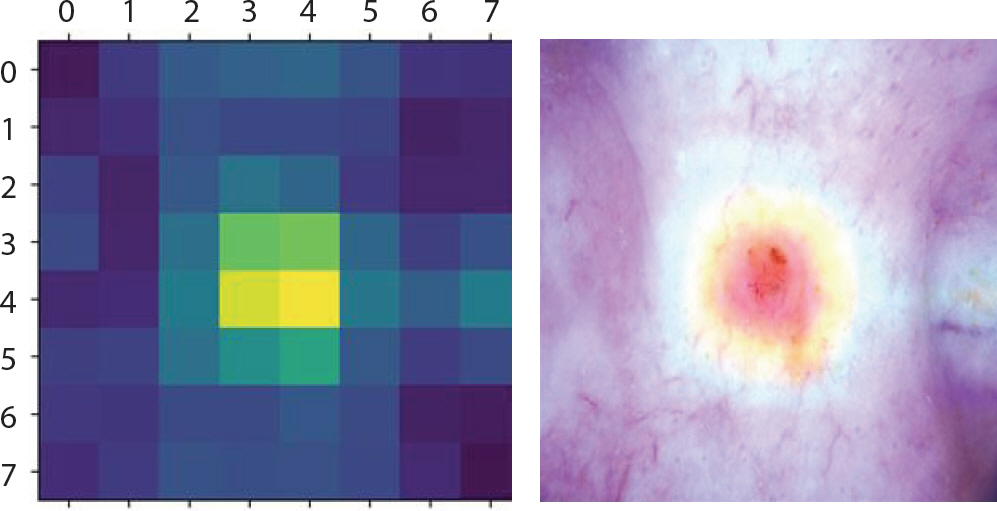
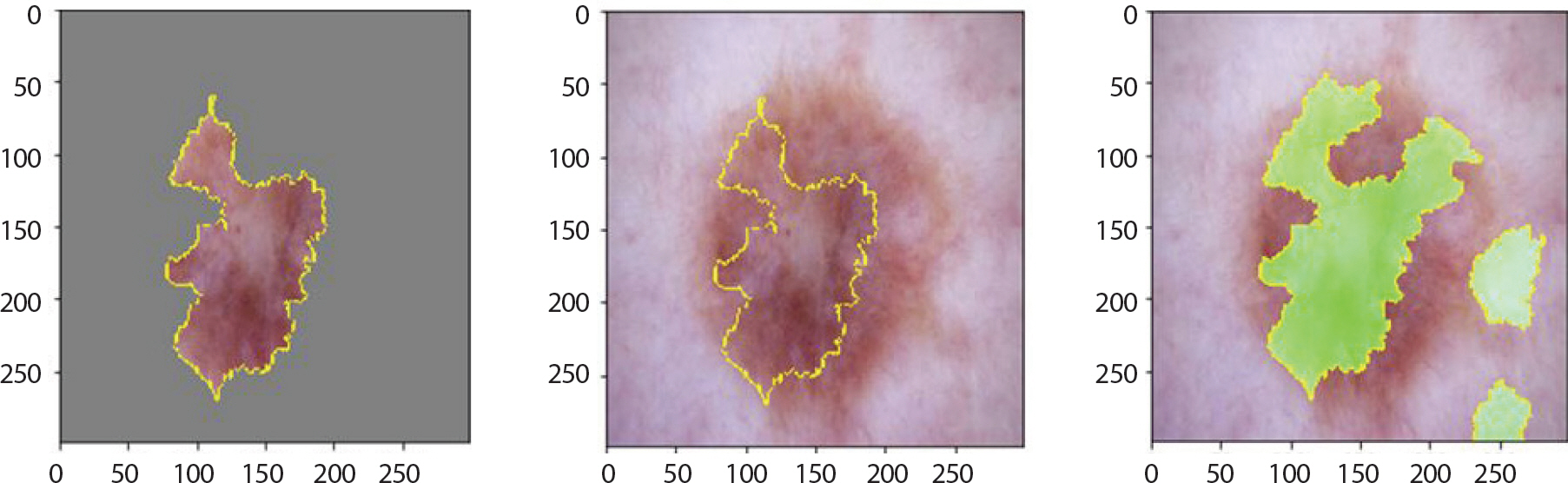
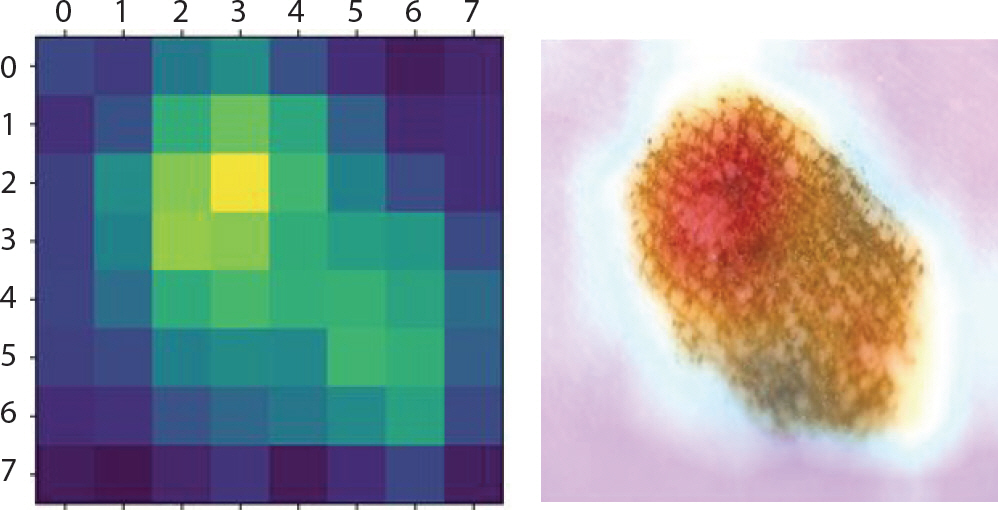
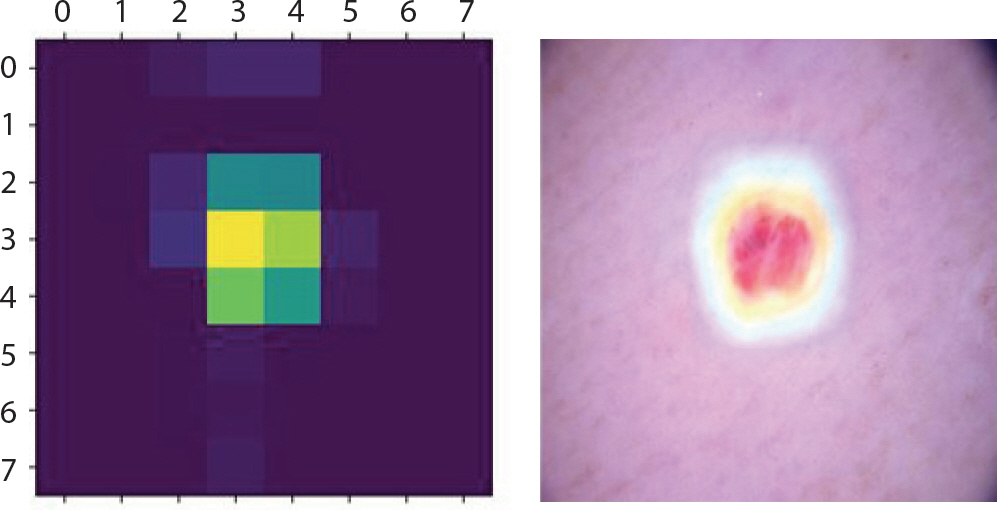
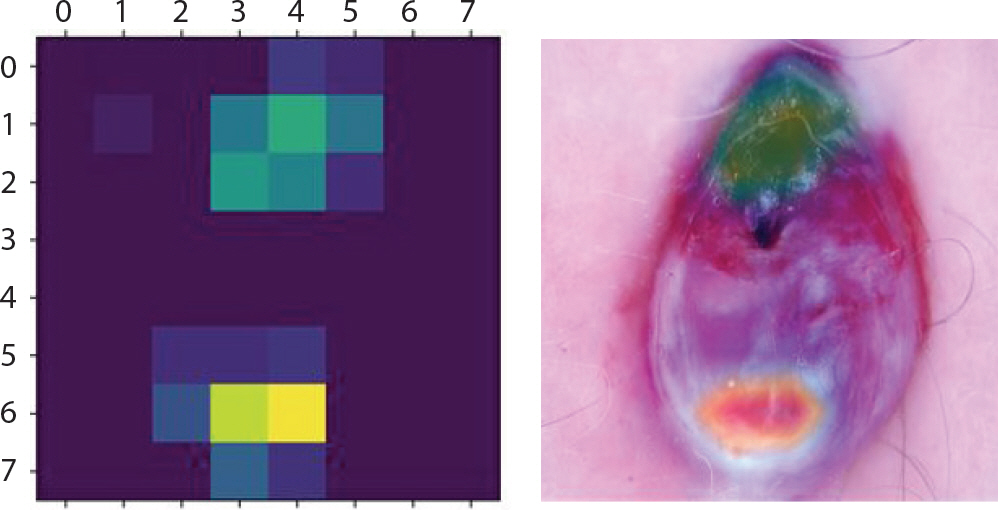
Figure 8은 LIME 기법을 적용하여 bcc에 속한 이미지에서 강조하고 있는 부분을 나타낸 것이다. 첫 번째 이미지는 분류하려는 이미지에서 가장 높은 확률을 갖고 도출해낸 레이블에 기여한 부분만 보였으며 두 번째 이미지는 해당 이미지 전체에 경계만 추가한 것이다. 세 번째 이미지에서 초록색은 1위의 레이블을 도출하는데 확률을 높이는 부분이며 빨간색이 확률을 낮추는 부분이다. Figure 9는 bcc에 속한 이미지에 Grad-CAM 기법을 적용하여 이를 이용해 원본 이미지에 히트맵(heatmap)을 더한 것이다. 가장 높은 확률을 갖는 레이블에서 강조하고 있는 부분이 노란색으로 나타났으며 원본 이미지에서는 그 부분이 빨간색으로 나타났다. 따라서 테스트 셋 이미지 데이터들 중 정답을 맞춘 이미지들의 다섯 가지 결과를 통해 각 병변의 고유한 특징 시각화를 하였다. 뿐만 아니라 1순위로 0.5에 이르는 확률의 오답 레이블, 2순위로 정답 레이블을 출력한 이미지는 출력된 두 순위의 특징이 비슷하기 때문이라 판단하여 이에 대해서도 LIME과 Grad-CAM을 적용했다.
akiec는 각화증인 만큼 표면이 건조하고 거칠며 적갈색의 원형모양이 1개에서 수십 개씩 생기고 기름기 있는 비늘과 딱지의 모양을 띤다. 초기에는 습진과 비슷하여 습진치료를 주로 받지만 잘 낫지 않기 때문에 초기에 조직검사를 통한 정확한 진단이 필요하다. Figure 10은 각각 거의 1에 가까운 0.99의 확률 값을 갖고 확실하게 분류하였으며 모두 akiec의 특징을 강조하고 있다. Figure 11은 0.57의 가장 높은 확률을 갖고 1순위로 mel이라 분류하였고 0.3의 확률을 갖고 2순위로 bkl이라 분류한 예시이다. 1순위 오답으로 mel이 가장 많았으며 mel로 분류하지만 이에 대한 1순위 확률 값이 0.5를 조금 넘는 정도이고 비슷한 확률 값으로는 2순위로 정답인 akiec를 도출했음을 통해 변색 된 부분에 대해 명확한 구분이 어려워 mel로 가장 많이 오분류하고 있음을 알 수 있었다.
Figure 10.
LIME (Local Interpretable Model-agnostic Explainions) result of akiec for skin cancer data.
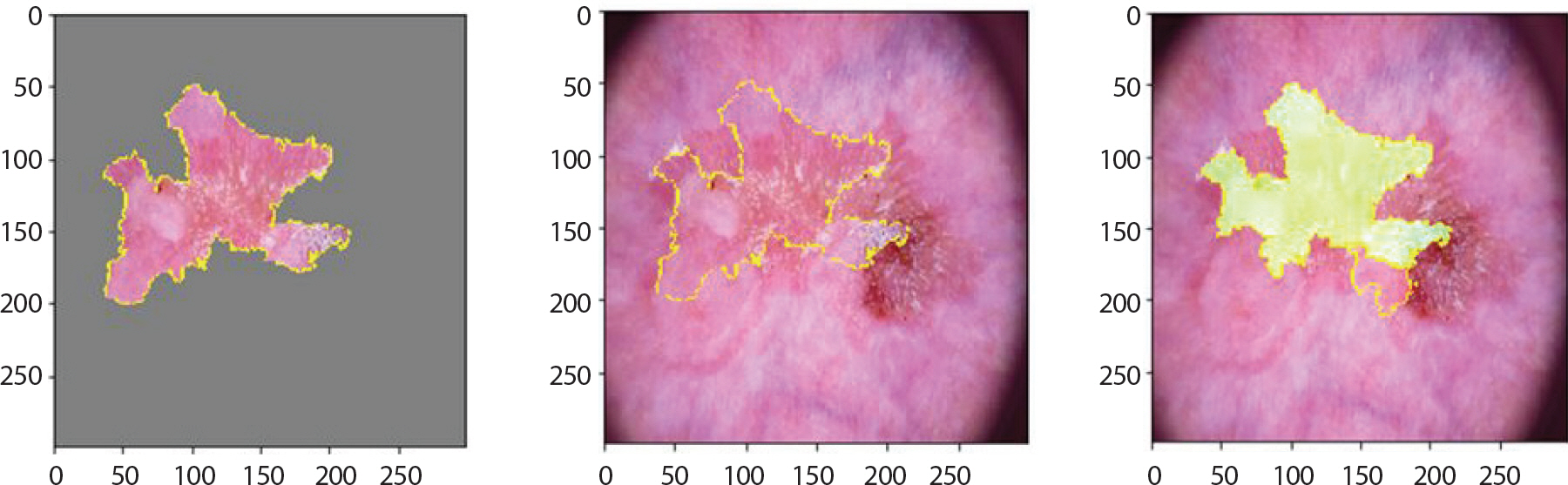
Figure 11.
Grad-CAM (Gradient-weighted Class Activation Mapping) result of akiec images which are incorrectly classified as mel for skin cancer data.
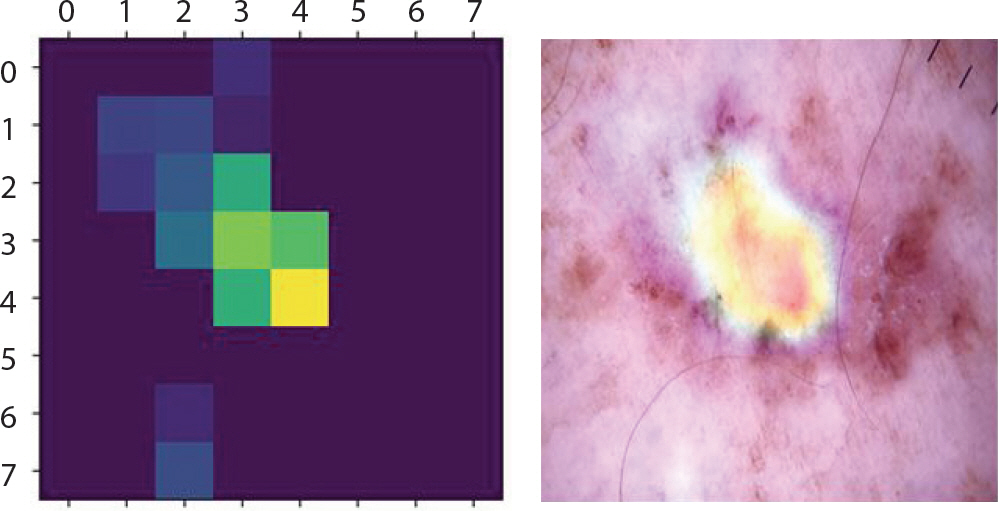
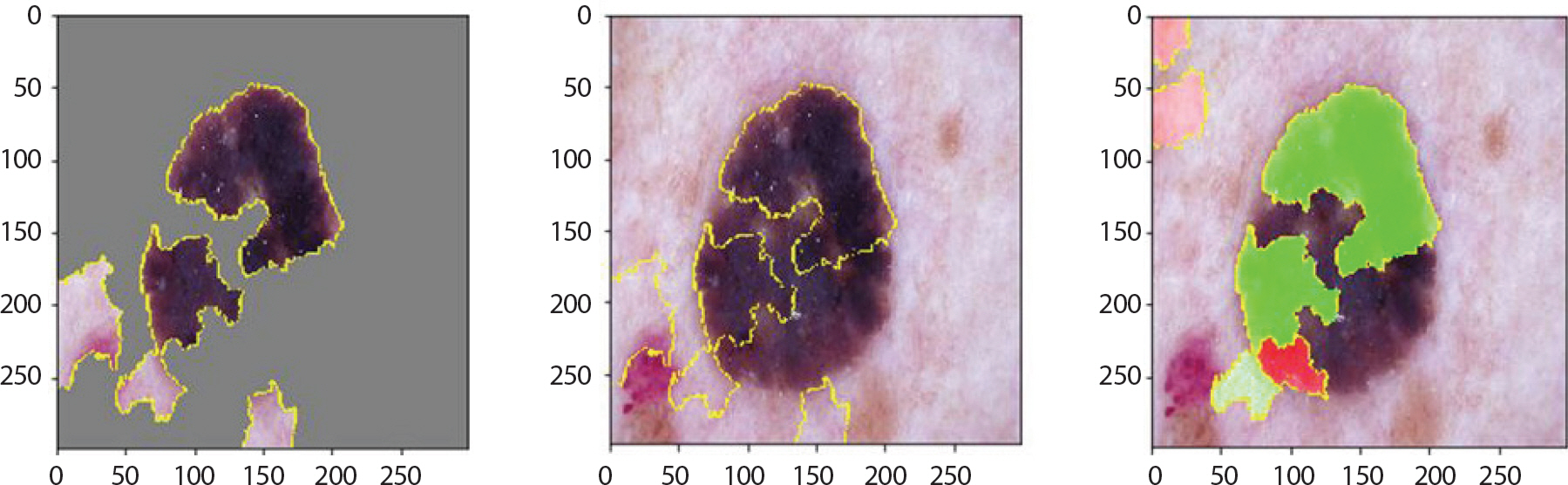
bcc는 출혈상처와 비슷하게 생겼으며 색깔은 주로 붉은 색이고 검은 점을 특징으로 한다. 각각 1.0과 0.77의 확률 값으로 잘 분류하였으며 Figure 12를 통해 이러한 특징을 강조하고 있음을 알 수 있다. 그러나 오답은 mel, bkl, nv 순으로 가장 많았다. Figure 13을 통해 실례를 볼 수 있다. 각각의 상단에서는 0.95의 확률 값으로 mel이라 오분류하였다. 1순위를 0.53의 확률 값으로 mel, 2순위를 0.46의 확률 값으로 nv라 오분류 하였다. 이 경우에서는 mel과 nv의 유사성에 의해 각각 0.5에 가까운 확률 값으로 정확한 분류를 하고 있지 못함을 알 수 있었다.
Figure 12.
LIME (Local Interpretable Model-agnostic Explainions) result of bcc for skin cancer data.
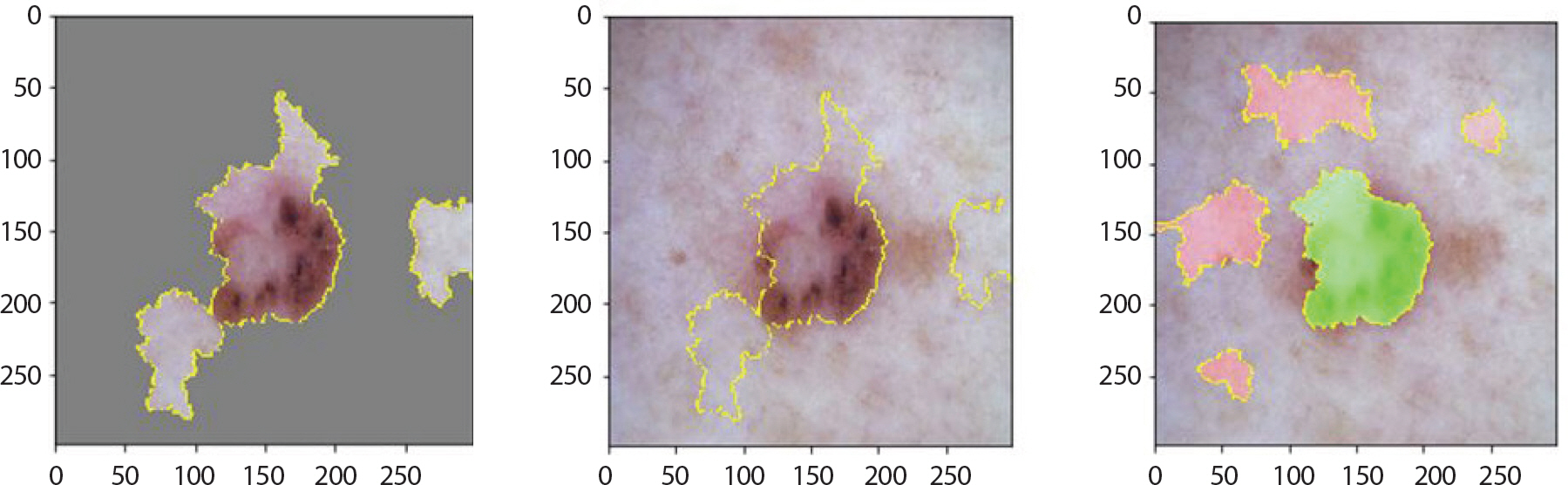
Figure 13.
LIME (Local Interpretable Model-agnostic Explainions) result of bcc images which are incorrectly classified as mel for skin cancer data.
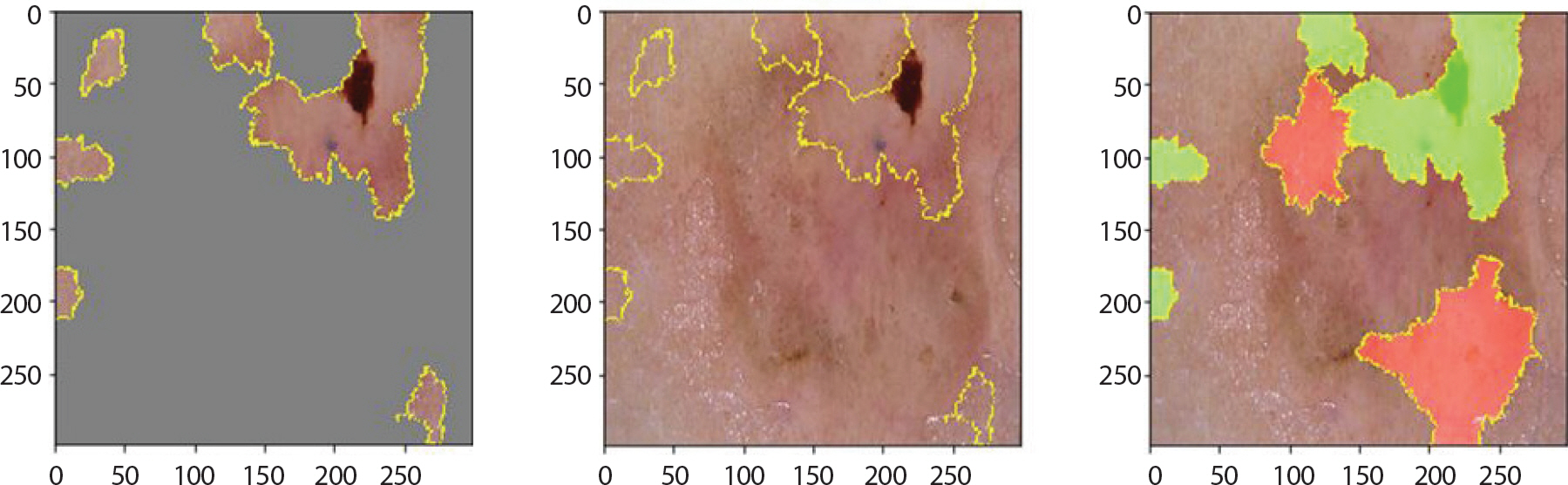
bkl은 검버섯과 비슷하게 생겨 저승꽃이라 불리기도 한다. 또한 작은 점들이 여러 개 있음을 알 수 있는데, Figure 14는 이런 특징들을 잘 강조하고 있음을 알 수 있다. 0.99의 확률 값으로 잘 분류하였다. 그러나 akiec와 마찬가지로 병변의 진행에 따라 검정색에 가까운 색으로 짙어지는데, 이런 이미지들은 mel과 nv 순으로 오분류하였으며 이는 Figure 15로부터 알 수 있다. 각각의 하단에서는 넓은 범위의 검정색에 가까운 진한 갈색의 모양을 띄고 있기 때문에 0.78의 확률 값으로 mel 로 오분류 하고 있음을 알 수 있었다.
Figure 14.
Grad-CAM (Gradient-weighted Class Activation Mapping) result of bkl for skin cancer data.
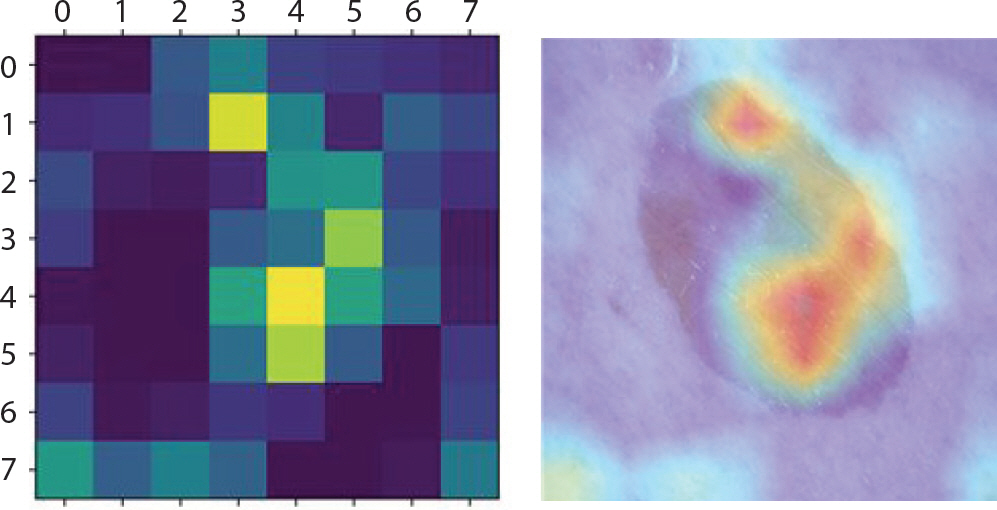
Figure 15.
LIME (Local Interpretable Model-agnostic Explainions) result of bkl images which are incorrectly classified as mel for skin cancer data.
df는 멍이 든 것 같이 대체적으로 피부색과 비슷한 색을 띄거나 분홍, 회색, 적갈색으로 나타내지만 병변이 진행되면서 변색되기도 한다. 대체적으로 정답을 맞췄으며 Figure 16을 통해 이런 특징을 강조하고 있음을 알 수 있었다. 상단과 하단에서는 각각 1.0, 0.7의 확률 값을 갖고 잘 분류함을 보였다. 그러나 Figure 17과 같이 검은 점이 있는 이미지에 대해서는 0.78의 확률로 흑색종(mel)이라 오분류했음을 알 수 있었다. 이 확률 값은 위에서 정답을 맞춘 그림이 도출한 확률인 0.70보다 더 큰 값이므로 이러한 특징을 보이는 df에 대해서 mel로 오분류할 가능성이 높음을 알 수 있었다.
Figure 17.
LIME (Local Interpretable Model-agnostic Explainions) result of df image which is incorrectly classified as mel for skin cancer data.
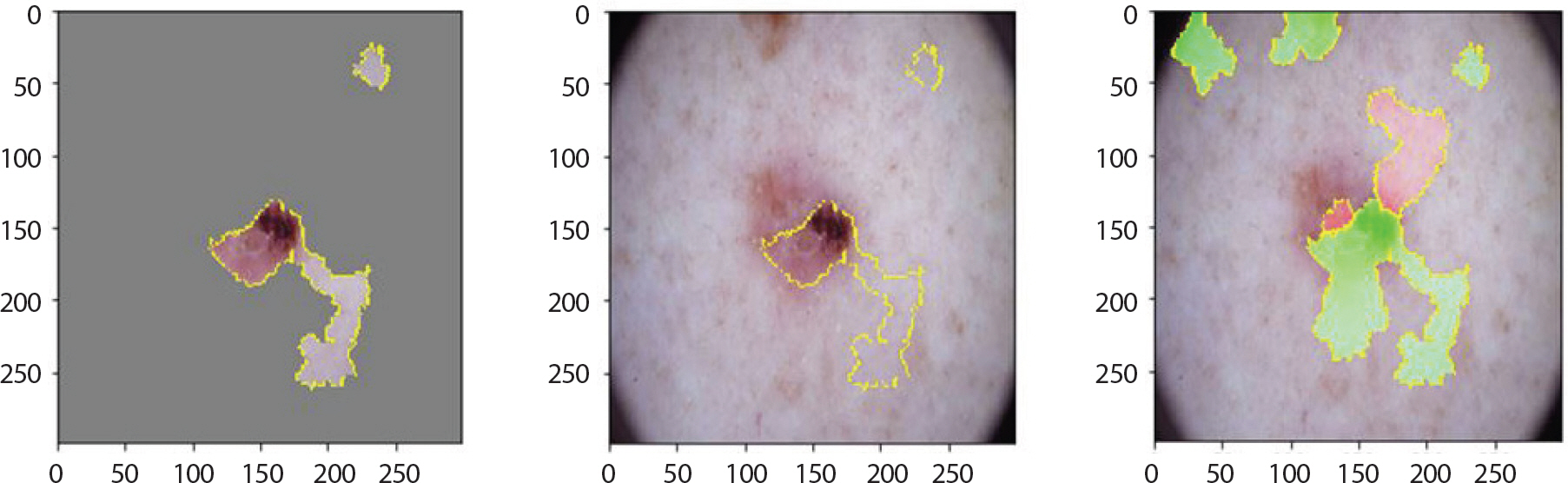
mel은 전이의 확률 및 속도가 매우 높고 빠르기 때문에 피부암 중에 서도 고위험군으로 분류되고 있다. 다른 병변에 비해 6 mm 이상의 비교적 큰 크기로 발병, 울퉁불퉁한 경계, 비대칭을 특징으로 하고 있으며 Figure 18은 1.0의 확률 값으로 잘 분류하였고 앞서 기술한 mel의 특징들을 강조하고 있음을 알 수 있었다. 오분류된 이미지들을 분석해보니 가장 높은 확률을 갖고 1순위로 추출된 레이블들은 nv와 bkl 순이었다. 그러나 아래의 Figure 19의 경우 0.60 정도의 가장 높은 확률 값으로 nv라 도출하였으며 2순위는 0.40 정도의 확률 값을 갖고 정답인 mel로 분류하였다. 각 값이 0.5보다 조금 작거나 크기 때문에 mel을 nv로 오분류할 가능성이 높지만 mel과 nv가 굉장히 비슷한 모습을 보이고 있음을 알 수 있었다.
Figure 18.
Grad-CAM (Gradient-weighted Class Activation Mapping) result of mel for skin cancer data.
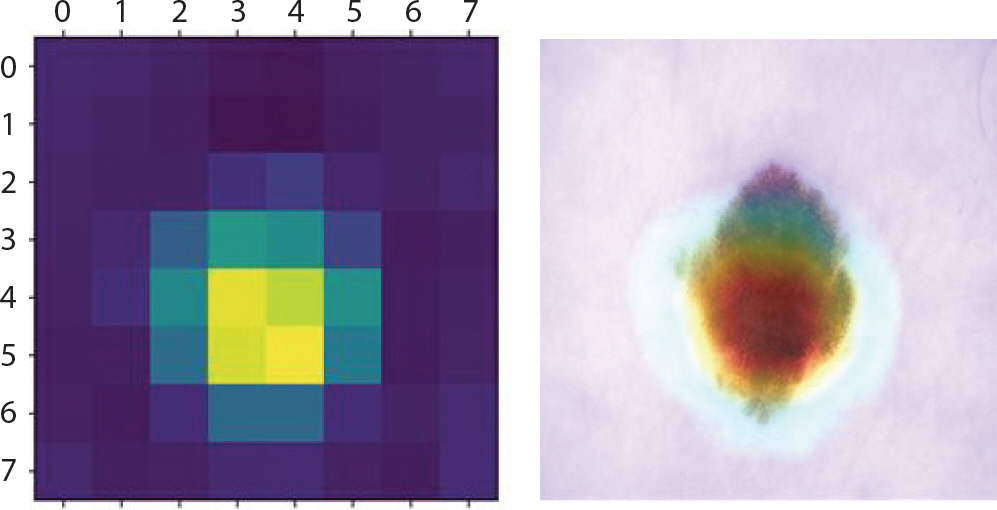
Figure 19.
LIME (Local Interpretable Model-agnostic Explainions) result of mel images which are incorrectly classified as nv for skin cancer data.
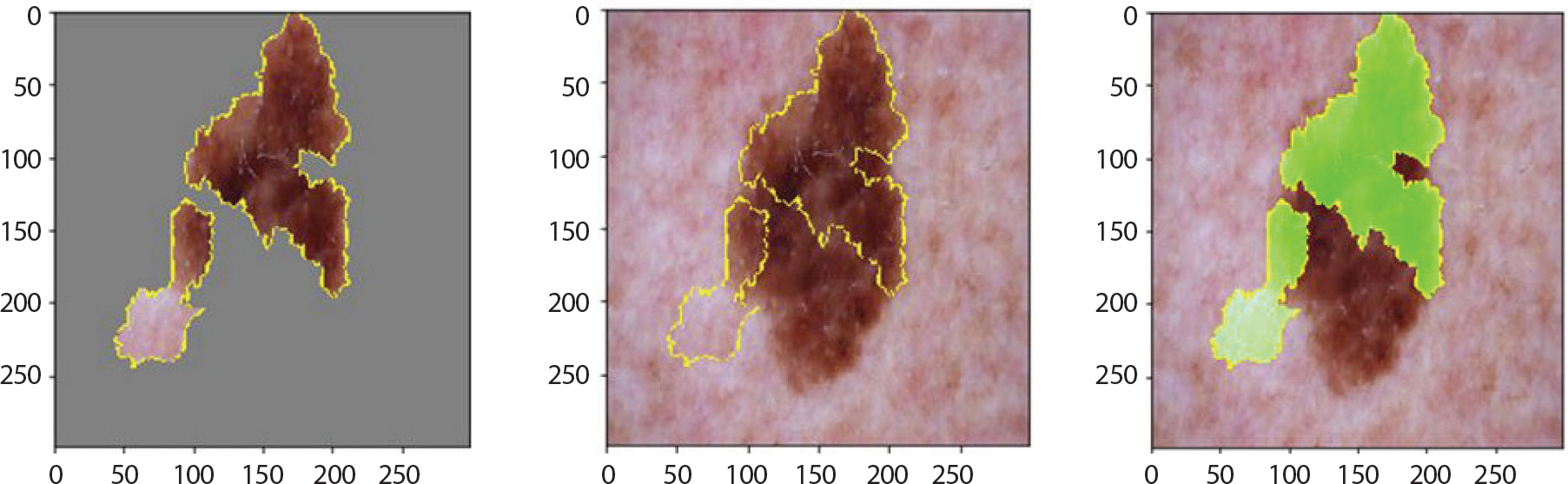
nv는 실제 mel 진행될 확률이 다른 병변에 비해 높고 모양도 mel과 비슷한 것이 특징이다. Figure 20은 1.0의 확률 값으로 정답을 맞추었고 이러한 특징을 강조하고 있음을 알 수 있었다. 오분류된 레이블들로는 bkl과 mel이 가장 많았다. 그리고 이런 이미지들을 분석해보니 Figure 21을 예로 들면, bkl이 1순위로 도출되었음에 불구하고 확률은 0.40이었다. 이어서 2순위인 mel의 확률은 0.34, 3순위로 정답인 nv의 확률은 0.25로 나타났다. 이러한 이유 때문에 어떠한 특징도 잡지 못하며 분류를 제대로 하고 있지 못함을 알 수 있다.
Figure 21.
LIME (Local Interpretable Model-agnostic Explainions) result of nv images which are incorrectly classified for skin cancer data.
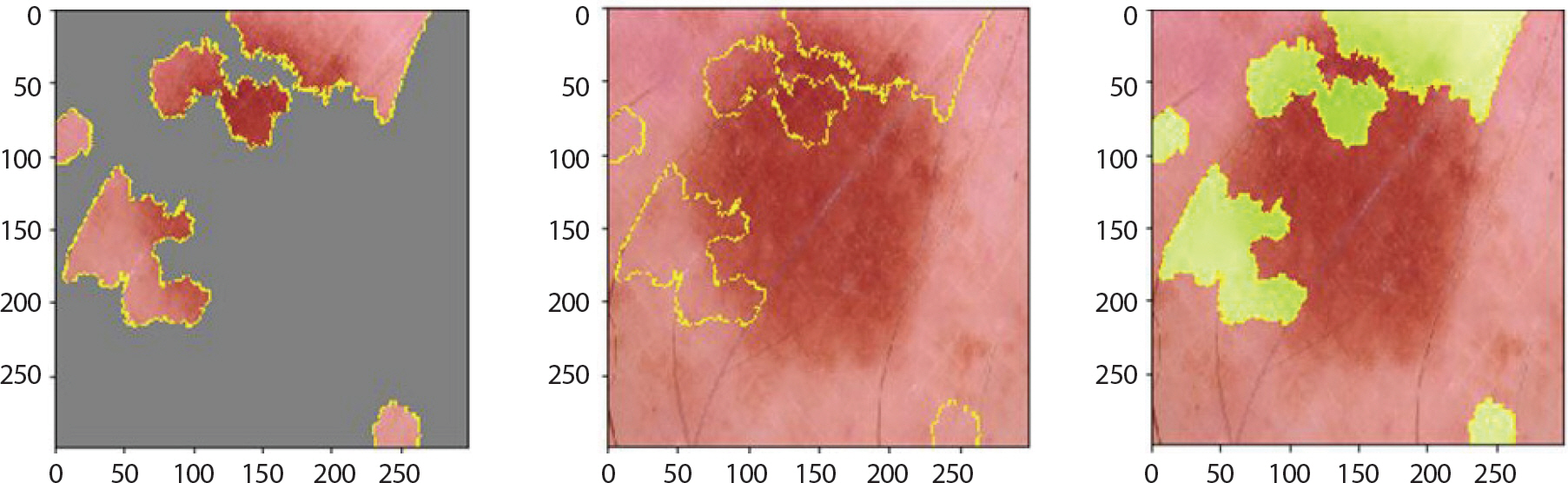
마지막으로 vasc는 주로 혈관 내에서 발생하기 때문에 대체적으로 붉은 덩어리의 모양을 띄는데 Figure 22는 1.0의 확률 값으로 정답을 잘 맞췄고 해당 병변의 특징을 잘 강조하고 있음을 알 수 있었다. 대체적으로 분류를 잘 하였지만 Figure 23과 같이 검은 점도 있는 이미지는 0.78의 확률 값을 갖고 bcc, 넓은 부위에 검정색을 보이는 이미지는 0.92의 확률 값을 갖고 mel로 오분류했음을 알 수 있었다.
고찰 및 결론
본 논문에서는 의학 분야에서의 정형·비정형 데이터를 이용한 설명 가능한 인공지능 기법에 관한 연구를 수행하였다. 먼저 정형 데이터는 중환자실에 입원한 환자들을 대상으로 48시간 동안 측정된 기록 데이터이다. 종속변수는 중환자실 내 사망 여부이며 어떤 변수들이 중환자실에서 사망하는데 얼마나 영향을 미치는지에 대한 변수 중요도를 추 출하였다. 사용된 기법들은 다중 작업 학습을 통한 증강 신경망, 랜덤 포레스트, extra tree, 그래디언트 부스팅, xgboost이다. 각 기법별로 변수 중요도 지표가 다름을 고려하여 모두 퍼센트 단위의 비율로 변환하였다. 변환한 데이터를 세 가지 방법으로 시각화하여 중요한 변수들을 한 눈에 파악할 수 있었다. 여러 가지 기법을 적용했기 때문에 오히려 시각화를 함으로써 각 기법별로 타겟변수에 영향을 미치는 입력변수들의 중요도를 기반으로 결과에 대한 해석을 더 잘 할 수 있었다.
이어서 비정형 데이터는 7가지 범주의 피부암 이미지 데이터이다. 설명 가능한 인공지능 기법 중 LIME과 Grad-CAM을 적용하여 가장 높은 확률의 레이블을 도출하는데 있어 기여한 부분을 강조하여 시각화하였다. 이를 통해 육안으로는 구별이 쉽지 않은 피부암의 특징들을 범주에 따라 한 눈에 파악할 수 있었다. 뿐만 아니라 bkl, mel, nv은 실제로도 매우 유사하게 생겼으며, 특히 nv은 병변이 진행됨에 따라 mel 로 판정받을 가능성이 높다. 또한 모든 피부암은 병변이 진행되면서 짙 은 갈색이나 검정색을 띄기 때문에, 실험 결과 위의 세 범주가 가장 높은 빈도의 오답으로 도출되었다. 이러한 정보들을 LIME과 Grad-CAM 을 적용하여 더욱 잘 파악할 수 있었다. 그렇기 때문에 초기에는 일반적인 점과 비슷한 모양으로 발병하기 때문에 피부암이 의심될 경우 내원 후 조기에 병변과 알맞은 치료법으로 대처해야할 필요가 있다.
환자 및 질병 데이터에 관한 분류 및 예측 결과는 생명이 직결되어 있는 만큼 높은 정확도도 중요하지만 왜 그러한 결과를 얻게 되었는지에 대한 설명을 통해 환자에게 신뢰를 안겨줄 필요가 있다. 이에 따라 본 논문에서는 의학 데이터의 변수 중요도를 이용한 분류 및 예측의 시각화 기법에 대한 연구를 수행하였다. 인공지능 기법 기반의 XAI 기법인 다중작업학습 증강신경망과 여러 가지 머신러닝 기법들에 수치형 데이터를 적용하여 각 기법별 변수 중요도를 추출할 수 있었다. 추출된 변수 중요도를 시각화하여 변수 관점에서 사망 결과에 대한 원인을 알 수 있었다. 그리고 LIME, Grad-CAM에 이미지 데이터를 적용하여 분류된 범주의 특징을 강조하는 부분의 피쳐의 중요도를 나타낼 수 있었다. 이를 통해 분류 및 예측에 있어 왜 그러한 결과가 나오게 되었는지 설명을 가능하게 해주고 해석을 용이하게 할 수 있다는 이점이 있었다. 따라서 본 연구를 통해 환자들이 합리적인 의사결정에 도모할 수 있을 것이라 기대하는 바이다.
또한 본 연구에서는 모델 적합에 사용된 변수 각각의 중요도에 대해서만 실험하였다. 기존의 머신러닝 기법들뿐만 아니라 다중작업학습 증강신경망 또한 변수들의 부분집합에 대한 중요도를 구할 수 있다[17]. 일례로 Gregorutti et al. [17]는 트리 모형에서의 기존 퍼뮤테이션 방법으로 계산하던 변수 중요도를 변수의 그룹으로 계산하는 방법을 제안하였다. 따라서 본 연구의 후속 연구도 마찬가지로 변수 각각이 아닌 변수들의 부분집합에 대한 중요도를 구하여 비교할 수 있는 연구의 필요성이 있다. 또한 수치형 데이터에는 LIME도 적용할 수 있으므로 함께 고려해볼 필요가 있다. 그리고 본 연구에서 수행한 의학 데이터뿐만 아니라 다른 도메인 데이터에도 XAI 기법을 적용해 볼 수 있으 며 계속해서 연구개발되고 있는 최신 XAI 기법들도 함께 적용해야 할 것이다.