서 론
임상시험을 계획하거나 수행할 때 통계적 설계를 위하여 참조하거나 따라야하는 규정과 가이드라인이 많이 존재한다. 그 중 International Council for Harmonisation of Technical Requirements for Phar-maceuticals for Human Use (ICH) E9은 임상시험에서의 통계 원칙에 대하여 다루고 있다. ICH E9은 임상시험에 적용되는 설계, 자료분석의 통계적 방법의 원칙들을 제시한 것으로 임상시험을 위한 설계, 수행, 분석, 평가의 방향을 제시하며, 신약 승인을 위한 자료 준비와 약물의 안전성 및 유효성을 평가하는데 도움을 주고자 만들어진 것이다[1]. 이 가이드라인은 전체 약 40페이지 정도밖에 되지 않지만, 다루는 내용은 방대하여 정확한 이해를 돕기 위하여 분야별 전문 서적을 통한 학습이 필요하기도 하다.
임상시험에 있어 통계학은 필수적이며, 설계에서부터, 데이터 모니터링 등을 거쳐 결과보고까지 정확하게 이해하고 이 내용들을 임상연구를 하고자하는 사람들이 이해하는 것은 굉장히 중요하다[2]. 그러나 임상시험 계획서나 보고서를 검토하거나 심사할 때 통계적 설계나 방법이 잘못 적용된 경우를 흔하게 찾아볼 수 있다. 특히, 표본크기 계산의 경우는 연구의 주 목적과 통계적 방법 등 서로 모순되는 경우를 쉽게 찾아볼 수 있다[3].
임상시험의 실패 원인은 다양하게 존재하는데 그 중 대표적인 원인 몇 가지를 보게 되면, 결과변수(outcome variable)를 잘못 정의했을 경우, 모집단(population) 정의를 잘못했을 경우, 그리고 시험대상자 수(sample size)를 잘못 계산했을 때이다.
이는 모두 연구계획단계에서 발생한 것으로 연구 계획단계의 올바르고 과학적인 설계가 얼마나 중요한지를 알 수 있게 한다. 따라서 본 논문에서는 임상연구를 함에 있어 이런 오류들을 피하고 올바르게 적용하여 임상시험의 과학적 설계를 하고 이로부터 얻어진 결과가 타당성과 신뢰성이 높은 결과를 도출하는데 도움이 되고자 한다.
연구 방법
연구계획서 작성 시 일반적 고려사항
임상시험을 수행하기 전에 하고자 하는 임상시험의 연구의 목적을 명확히 하여야 한다. 임상시험에는 많은 분야의 전공자들이 함께 연구에 참여하기 때문에 연구의 목적을 명확히 전달하는 것이 연구시작 단계에서 있어 가장 중요한 일이라고 할 수 있다. 왜냐하면, 연구의 주 목적(primary objective)이 정해지면, 그 목적을 검정하기 위한 연구가설이 세워지고, 이 때 평가되어질 주평가변수(primary endpoint)가 정의된다. 또한 주평가변수를 얻기 위한 실험설계(experimental design)가 계획되고, 이로부터 통계학적 분석방법이 정해진다. 그러면 이때 정해진 통계방법을 이용하여 시험대상자수를 계산하게 되고, 임상시험이 종료되면 이들로부터 얻은 자료를 가지고 연구가설이 입증되는지를 검정하는 것이다. 따라서 연구의 목적이 명확하지 않으면, 임상시험을 수행하기 위한 설계에 있어 많은 부분에서 오류가 발생하게 되고, 이렇게 잘못된 설계는 임상시험 실패로 이끄는 아주 치명적인 원인이 될 수 있다.
본 논문에서 이해를 돕기 위한 예제는 서로 독립인 두 군(시험군과 대조군)을 비교하면서 실험 설계는 병행설계일 때, 주 평가변수인 일차평가변수가 하나 일 때, 그리고 두 군의 차이값(시험군-대조군)이 0보다 클 때 시험군의 효과가 좋은 것으로 가정했다.
유의수준(significance level) 설정
확증연구는 연구의 주 목적을 입증하기 위한 절차를 밟기 때문에 연구계획단계에서 제1종 오류(type I error)의 최대 허용치인 유의수준(α)을 미리 정하는 것은 중요한 과정 중의 하나이다. 정해진 유의수준을 이용하여 시험대상자 수(표본크기, sample size) 계산 및 통계적 가설검정(hypothesis test)에 사용되기 때문이다. 가설검정 시 양측검정(two-sided test)에서는 0.05를 단측 검정(one-sided test)에서는 0.025라는 값을 보편적으로 사용하고 있지만, 이것은 정해진 값은 아니다. 경 험적으로 사용되는 값이며, 다만, 그 값이 클 경우에는 귀무가설(H0, null hypothesis)이 참일 때 귀무가설을 기각하게 되는 제1종 오류가 커져서 잘못된 의사결정을 하게 될 확률이 높아진다. 유의수준 설정에서 주로 발생하는 오류와 해결방법을 동시에 설명하면 다음과 같다.
첫째, 미리 정한 유의수준 값에 의하여 시험대상자수가 결정되고, 가설검정에도 사용된다. 미리 정한 유의수준으로 표본크기 계산에 반영하고, 가설검정 시(신뢰구간 계산 포함)에도 같은 값의 유의수준을 적용하여야 한다. 주연구가설이 여러 개 이거나 일차평가변수가 여러 개일 경우, 보정의 문제가 발생할 수 있다. 둘째, 주 평가변수, 주로 일차평가변수를 평가함에 적용된다. 셋째, 연구의 주 목적에 대한 가설검정을 할 때, 최종 의사결정시 미리 정한 유의수준이 사용되며, 이때 정규성검정, 등분산성검정, 교호작용검정 등과 같이 최종 가설검정 중간 단계에 사용될 유의수준은 따로 정해서 기술하여야 한다.
통계학적 검정력(statistical power) 설정
검정력은 대립가설(H1, alternative hypothesis)이 참일 때 이를 받아들일 확률이다. 연구의 주 목적(primary study objective)을 대립가설로 세우는 경우가 대부분인데, 이때 검정력이 높다는 것은 하고자하는 임상시험을 통하여 연구의 주 목적을 잘 증명한다고 해석할 수 있다. 따라서 시험대상자 수를 계산할 때, 유의수준과 더불어 적절한 검정력을 얻기 위한 수를 계산하는 것은 의도하고자 하는 연구에 필요한 대상자수의 과학적이고 적절한 수를 계산할 때 꼭 반영되어져야 하는 이유가 된다. 검정력 설정에서 주로 발생하는 오류는 다음과 같다.
첫째, 시험대상자수를 높이기 위하여 검정력을 높이는 경우가 간혹 있다. 일반적으로 최소 경험수치는 80%인데, 단순하게 수를 늘이기 위한 목적으로 95% 등으로 그 값을 크게 정하는 경우가 있다. 이것을 틀린 접근이라고 할 수는 없지만 검정력을 높이는 본연의 이유에 대하여 고민할 필요가 있다. 둘째, 임상시험이 끝난 뒤 검정력 계산을 할 때가 있는데 이는 별 의미가 없다[3]. 이미 종료된 임상시험의 결과로 검정력을 계산하는 것보다는 효과크기의 임상적 의미, 시험대상자수의 적절성 등을 고찰하는 것이 더 의미가 있다.
비교형태(comparison of type)에 따른 가설설정
임상시험은 탐색시험(exploratory trial)과 확증시험(confirmatory tri-al)으로 나뉠 수 있다. 탐색적 임상시험은 미리 정의된 가설을 검정하는 것이 목적이 아닐 수도 있고 또는 자료의 탐색을 통하여 새로운 가설을 세울 수도 있다[1]. 그러하다보니 임상시험에서 주로 사용하는 비교 형태는 효과차이를 확인하고자 하는 효과차이 검정(equality test)을 많이 하게 된다. 반면, 확증시험은 탐색시험의 결과에 근거하여 분명하고 정확한 목적을 가지고 연구를 수행하기 때문에, 우월성 임상시험 (superiority trial), 비열등성 임상시험(non-inferiority trial), 그리고 동등성 임상시험(equivalence trial)을 주로 하게 된다. 효과차이 임상시험은 양측가설이고 우월성 임상시험, 비열등성 임상시험 그리고 동등성 임상시험은 단측가설이다[4]. 비교형태에 따른 올바른 가설 설정이 중요한 이유는 이는 표본크기 계산과 가설검정시에 반영되기 때문이다. 가설 설정에 있어 주로 발생하는 오류는 아래와 같다.
첫째, 우월성 임상시험의 가설을 양측가설로 설정하는 계획서를 쉽게 찾아볼 수 있는데, 우월성 임상시험은 단측가설로 세워야 한다. 둘째, 비열등성 임상시험의 대립가설에 등호(=)를 포함하는 경우가 간혹 있는데, 대립가설에는 등호(=)를 넣지 않는다. 셋째, 동등성 임상시험을 양측가설로 오인하는 경우가 자주 발생하는데, 동등성 임상시험은 단측 가설을 두 번(two one-sided test)하는 것이다. 넷째, 연구의 주 목적을 가설로 세울 때 일차평가변수(primary endpoint)를 사용하여 설정하여야 한다.
일차평가변수(primary variable, primary endpoint)
일차평가변수는 연구의 주 목적을 검정하기 위하여 정의되는 주요 변수이며[1], 질병에 따라 또는 연구의 목적에 따라 평가하는 변수는 여러 가지 있다. 이 일차평가변수는 연구계획서 전체의 흐름을 잡아간다. 일차평가변수 설정시 오류는 주로 다음과 같다.
첫째, 일차평가변수를 정의할 때는 치료의 효과를 평가할 수 있는 치료시점을 반영하여 정의해야한다. 둘째, 차이값을 사용할 때는 전에서 후를 빼는 값인지 후에서 전을 빼는 값인지 명확하게 정의해야하고, 시험군에서 대조군을 빼는지 대조군에서 시험군을 빼는지 정의가 명확해야한다. 이 부분은 표본크기를 추정할 때와 가설검정할 때 올바르게 적용되어야 한다. 셋째, 일차평가변수를 평가하는 방법은 주로 신뢰구간으로 하게 되는데, 어떤 통계학적 방법으로 계산하는지 구체적으로 작성하여야 한다.
비뚤림(bias)을 없애는 설계 단계에서의 기법
임상시험에서 비뚤림을 피하기 위한 이루어지는 주요 설계 방법은 눈가림법(blinding)과 무작위배정(randomization)이며, 이 두 가지는 규제기관으로부터 판매허가 신청을 위한 비교 임상시험의 일반적 특성이다[1]. 무작위배정과 눈가림법에서 종종 발생하는 오류는 다음과 같다.
무작위배정에서는 첫째, 대상자들에게 어떤 처치에 노출되는지 유추할 가능성을 조금이라도 없애기 위하여 연구계획서에 블록 크기(block size)를 공개하면 안 된다. 둘째, 무작위배정 프로그램에 사용한 초기값(seed number)을 공개하면 안 된다. 셋째, 층화요인을 고려하였을 경우, 이 층화요인들은 자료의 주 분석에서 고려되어져야 한다.
대조 임상시험들은 대부분 이중눈가림(double-blind)을 시행하는데, 어떤 경우에는 이상적인 이중눈가림을 실현하는 것은 매우 어려울 수 있다. 이 경우에는 단일눈가림(single-blind)이나 공개(open) 임상시험 설계를 해야 하고 이때는 비뚤림을 최소화할 수 있는 방법, 예를 들어, 평가자 눈가림(assessor-blind)이나 주평가변수의 객관화 등에 신경을 써야 한다. 눈가림법에서 종종 들어나는 오류는 다음과 같다.
첫째, 단일눈가림 임상시험에서 평가자 눈가림을 더했을 경우를 이중눈가림으로 기술하는 경우가 종종 있는데, 이 방법은 주평가변수 평가시 발생할 수 있는 비뚤림을 최소화하기 위한 보완책일 뿐 이중맹검이 아니고, 단일맹검이다. 둘째, 임상시험 수행에서 사실상 이중눈가림이 유지 되지 않지만, 이중눈가림으로 설계하고 진행하는 경우가 간혹 있다. 이중눈가림이 어려운 경우에는 단일눈가림을 하고 비뚤림을 최소화할 수 있는 보완책을 대비하는 것이 적절하다.
시험대상자수 계산(sample size calculations)
시험대상자수(표본 크기) 계산은 일반적으로 연구의 주 목적에 의하여 계산되어진다. 즉, 하고자 하는 연구의 주 목적을 입증하기 위하여 정당한 시험대상자 수를 계산하는 것으로 임상계획단계에서 가장 중요한 부분이라고도 할 수 있다. 시험대상자수 계산 시 주로 발생하는 오류는 다음과 같다.
첫째, 하고자 하는 연구가 최초의 연구이거나 유사연구가 없을 때, 알고 있는 정보만으로 계산하여 연구의 주 목적을 올바르게 반영하지 못한다. 이런 경우에는 예비연구(pilot study), 중간분석(interim analy-sis) 등을 통하여 표본크기를 추정하거나 시험방법을 적응적 임상시험(adaptive design) 등으로 설계하여 해결 방법을 찾을 수 있다. 둘째, 시험대상자수를 줄이기 위하여 일차평가변수가 아닌 다른 평가변수로 계산하는 경우가 있는데, 특별한 사유가 없는 한 일차평가변수로 표본크기를 계산해야 한다. 셋째, 일차평가변수의 통계 주 분석법이랑 시험대상자수 공식이 전혀 무관한 경우가 간혹 발생한다. 시험대상자수 계산을 위하여 검정력 분석(power analysis) 방법으로 계산하였다면 통계분석법에 맞는 표본크기 공식을 이용하여 계산하여야 한다. 넷째, 모수 추정 시 모집단(population)을 반영하지 못한 경우가 발생하기도 한다. 시험대상자수 계산을 위하여 모수 추정 시에는 모집단을 잘 대표할 수 있는 모수 추정치를 사용하는 것이 중요하다. 다섯째, 시험대상자수는 올림으로 계산하여야 하며, 버림이나 반올림을 하지 않는다. 여섯째, 동등성 임상시험(equivalence trial)은 단측 검정을 두 번 하기 때문에 검정력을 보정하여야 하며, 표본크기 계산 시 반영되어야 한다.
통계분석군(statistical analysis set) 정의
임상시험이 끝나고 통계분석군을 정의해야 한다. 통계분석군이라는 것은 임상시험에 참여한 대상자들의 연구계획서 위반 및 위배 내용 등을 기준으로 해당 대상자를 연구계획서대로 잘 순응한 군(Per-Proto-col Set, PPS)에 포함시킬지 아니면 이들을 포함하면서 연구계획서 위반 및 위배는 했지만, 주요한 내용들이 아닌 경우도 포함하는 FAS (Full Analysis Set)에 포함할지 정해야 한다[5]. PPS와 FAS로 분리할 때 구분 기준은 주평가변수를 평가함에 있어 해당 위반 사항이 얼마나 중요하게 영향 미치는 지를 기준으로 판단한다. 주로 발생하는 오류는 다음과 같다.
첫째, 통계분석군을 정하는 블라인드 미팅(blind meeting)은 임상자료관리(clinical data management)가 끝나고 자료분석하기 전에 이루어져야 한다. 통계분석 도중이나 주유결과를 알게 된 이후에 하는 것은 대단히 부적절하다. 둘째, 블라인드 미팅 시에는 각 대상자들의 무작위코드는 공개하지 않는다. 무작위배정코드가 공개될 경우, 해당 시험자의 위반 또는 위배 내용을 왜곡되게 해석하여 결과를 유리하게 할 수 있는 분석군으로 정의할 수 있기 때문이다. 셋째, 주요한 사항을 위반한다고 했을 때, 주요한 사항이 무엇인지를 계획단계에 미리 정해야 한다. 이유는 주요한 위반사항을 어떻게 정의하느냐에 따라 연구결과가 달라질 수 있기 때문이다.
일차평가변수에 대한 가설검정
비교형태에 따른 가설검정에 사용되는 주 방법은 신뢰구간을 이용하는 것이다. 만약 시험군과 대조군의 차이값(시험군-대조군)이 0보다 클 때 개선되었다고 할 수 있다면 우월성은 신뢰구간 하한치가 우월성 한계치보다 커야하고 비열등성은 하한치가 비열등성한계치보다 커야하고 동등성은 상한치와 하한치가 동등성한계치 안에 들어와야 한다[1,6]. 이때 등호는 해당되지 않는다. 즉, 대립가설에 등호는 없다. 비교형태에 따른 가설은 Table 1에 주어져 있다.
Table 1
Hypothesis according to the type of comparisons
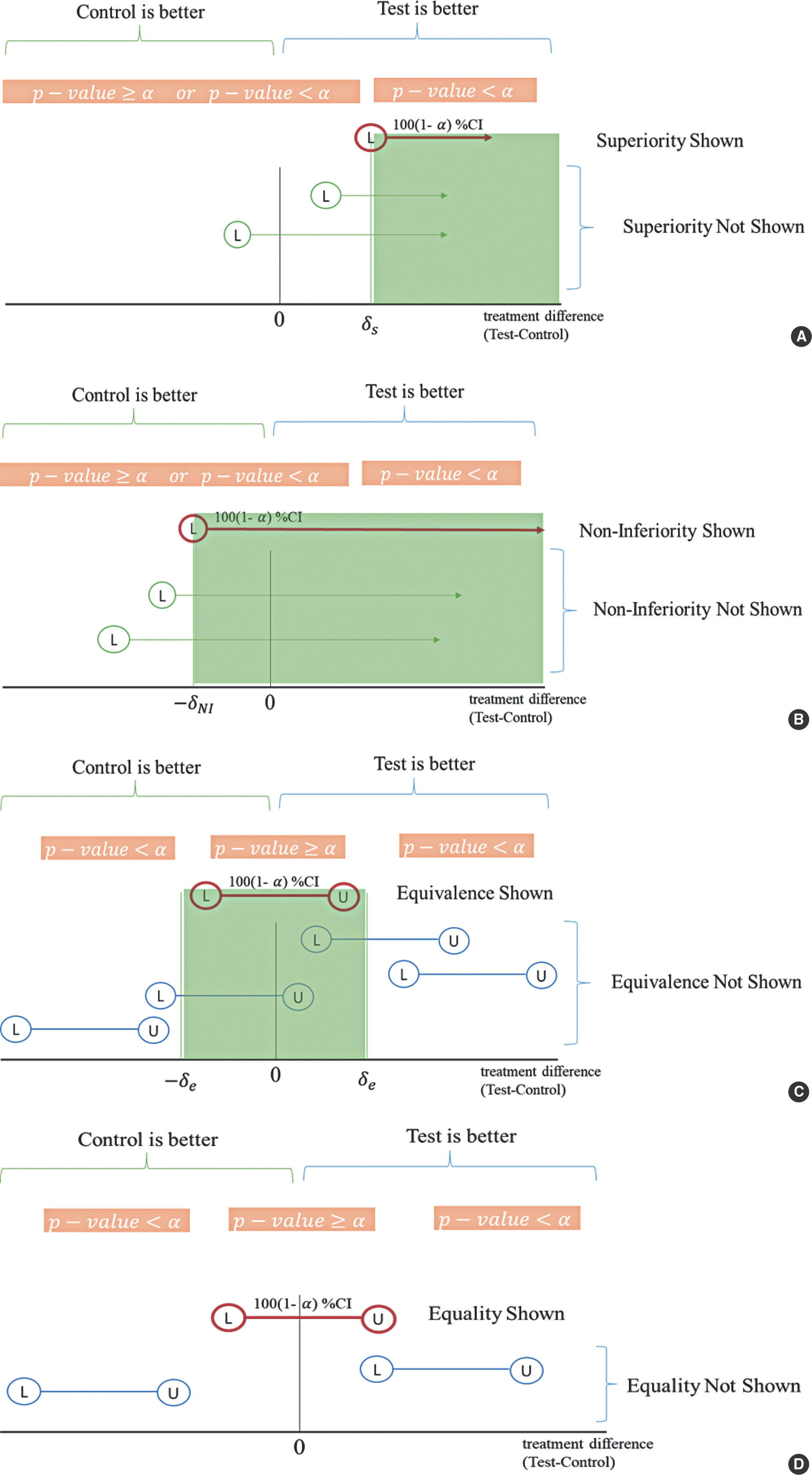
혹자는 유의확률(p-value)이 주어진 유의수준보다 적으면 비열등성, 우월성 그리고 동등성을 만족한다고 착각을 한다. 사실은 그렇지 않다. Figure 1A를 보면, 우월성 임상시험의 경우, 신뢰구간의 하한치는 미리 정의된 우월성 한계치(δ s)보다 커야하며, 이 경우 유의확률이 주어진 유의수준보다 적다. Figure 1B는 비열등성 임상시험에 해당되며, 신뢰구간의 하한치가 미리 정의된 비열등성한계치(δ NI)보다 커야하며, 이 경우 유의확률은 주어진 유의수준보다 클 수도 있고, 작을 수도 있다. Figure 1C는 동등성 임상시험에 해당되며, 신뢰구간의 하한치 및 상한치 둘 다 미리 정의된 동등성 한계치(δ e)안에 들어와야 한다. 이 경우, 유의확률이 유의수준보다 크다. Figure 1D의 경우는 효과차이 검정에 대한 것으로 신뢰구간에 0을 포함하고 있으면, 효과차이가 없다는 뜻이며, 0을 포함하지 않으면 비교군과의 효과차이가 있음을 의미한다. 이때 전자는 유의확률이 주어진 유의수준보다 큰 값을 가지며, 후자의 경우는 주어진 유의수준보다 작은 값을 가진다.
Figure 1
Hypothesis test according to the comparison type. (A) Test for superiority trial. (B) Test for non-inferiority test, (C) Test for equivalence test, (D) Equality test. CI, confidence interval; L, lower bound of a CI; U, upper bound of CI; α, level of significance. Empty circle means that it does not belong the compared value such as margins.
이때 주로 발생하는 오류는 다음과 같다.
첫째, 단측 가설을 유의확률로만 판단하는 오류가 종종 발생한다. 효과차이 임상시험을 제외하고 우월성, 비열등성, 그리고 동등성 임상시험은 단측 가설이므로 신뢰구간으로 판단한다.
둘째, 신뢰구간의 하한값 또는 상한값과 임상적 한계치(우월성, 비열등성, 그리고 동등성 한계치)를 비교할 때 그 값은 포함되면 안된다.
결측치(missing value) 처리
임상시험의 경우 결측치 발생은 흔하게 일어난다. 결측치를 어떻게 처리할 지에 대한 통계학적 방법 또한 다양하다. 따라서 연구계획서에 미리 그 방법을 정하지 않으면 결과해석 시 유리한 방향을 유도하는 방법으로 처리할 수도 있다. 결측치에 대한 일반적 오류는 다음과 같다. 첫째, 결측치 처리에 대한 방법론이 명확하게 기술되어 있지 않는 경우가 종종 있다. 결측치 처리 방법에 따라 결과가 달라질 수 있기 때문에 그 방법은 명확하게 연구계획단계에서 기술되어야 한다. 둘째, 결측치 처리를 적용하게 되는 평가변수들을 설정하여야 한다. 대부분의 경우, 일차평가변수에 한해 많이 하지만, 이차 평가변수에서도 결측치 처리가 가능하므로 구체적인 기술이 필요하다. 실험실자료의 경우는 결측처리를 하지 않고 ‘얻어진 값 그대로 사용하는 것’이 일반적이기도 하다. 셋째, 결측치 처리를 위하여 여러 방법을 사용할 경우, 민감도 분석(sensitivity analysis)을 할 필요가 있다. 넷째, Last Observation Car-ried Forward (LOCF)가 모든 평가변수에 적절한 것은 아니다. 일반적으로 이 방법이 보수적결과를 유도할 때가 많아서 사용의 빈도가 높을 뿐이다.
공분산분석(ANCOVA, Analysis of Covariance)
통계분석방법에 대한 오류는 여러 논문에서도 언급을 해왔다. 본 논문에서는 연속형변수(continuous variable)가 일차평가변수인 임상시험에서 가장 많이 사용되는 공분산분석에 대하여 논하고자 한다. 공분산분석에서는 공변량(covariates)을 미리 설정하는 것이 중요한데, 공변량이 임상시험 주 평가변수의 결과에 영향을 많이 미치기 때문이다[7]. 공분산 분석에 있어 주로 발생하는 오류는 다음과 같다.
첫째, 연구계획서에 공변량을 미리 정하지 않고 분석시 여러 가지 공변량을 적용하는 경우가 있다. 어떤 공변량을 사용하느냐에 따라 결과가 달라지기 때문에 공변량은 연구계획 시 미리 정해야 한다. 둘째, 공분산분석을 할 경우 산술평균이 아닌 최소제곱평균(Least Square Mean)을 제시하여야 한다. 셋째, 주 분석이 공분산분석일 경우, 신뢰구간의 계산도 공분산분석에 의하여 계산되어져야 한다. 넷째, 공변량이 처리에 영향을 받지 않아야 한다. 이 부분은 통계분석단계에서 검정이 되어야 한다. 다섯째, 공변량의 효과가 있는지 없는지 통계분 석단계에서 검정이 되어야 한다. 여섯째, 교호작용을 확인할 때 유의수준은 얼마로 할지 연구계획단계에 미리 설정해야한다. 일곱 번째, 공변량의 효과와 교호작용의 효과를 확인한 후 최종 모형에 해당 내용을 반영할지 안 할지 정한 다음 최종 분석 결과를 결과로 제시하여야 한다.
고찰 및 결론
임상시험의 종류는 목표로 하는 질병, 연구의 단계, 의약품개발인지, 의료기기 개발인지, 탐색단계인지, 확증단계인지, 대조군의 설정 등 아주 많은 상황에 영향을 받게 된다. 또한 연구설계를 잘 계획하여도 현실적으로 수행가능여부를 고려할 때 비용-효용(cost-effectiveness) 등의 문제로 trade-off가 발생하기도 한다[3]. 각 상황에 맞는 통계학적 설계도 다양하기 때문에 그 방법론을 한 가지로 정의해서 설명하는 것이 쉽지 않다. 대부분 가장 많이 사용하고 간단한 설계를 통하여 의약품이나 의료기기 임상시험을 설계할 것을 추천하게 되는데, 이는 의사결정시 복잡한 가정을 피할 수 있기 때문이기도 하다.
본 논문에서는 연구의 복잡성 및 다양성 등 여러 가지 상황에 상관없이 흔하게 발생하는 오류를 다루었고, 여기서 다룬 내용 이외에도 임상시험 설계에서부터 결과보고까지 발생하는 통계학적 오류가 더 있다. 이러한 오류들을 최소화할 수 있는 가장 중요한 것은 연구의 주 목적을 명확하게 언급하는 것이다. 그리고 그로부터 가설설정, 주평가변수정의, 실험설계, 자료분석의 통계적 방법, 표본크기 설정까지 모두 영향을 준다는 것을 이해하고 올바르게 적용하는 것이다.











